想在中考数学中稳拿高分？几何部分绝对是关键战场。今天为你系统梳理中考数学最常考的12类几何模型，掌握它们，你就能在错综复杂的图形中找到突破口，解题思路瞬间清晰。
从基础的全等三角形模型出发，这是几何证明的基石，涉及平移、对称、旋转等多种变换形式。
相似三角形模型则常隐藏在复杂的图形组合中，需要你敏锐识别对应边角关系。
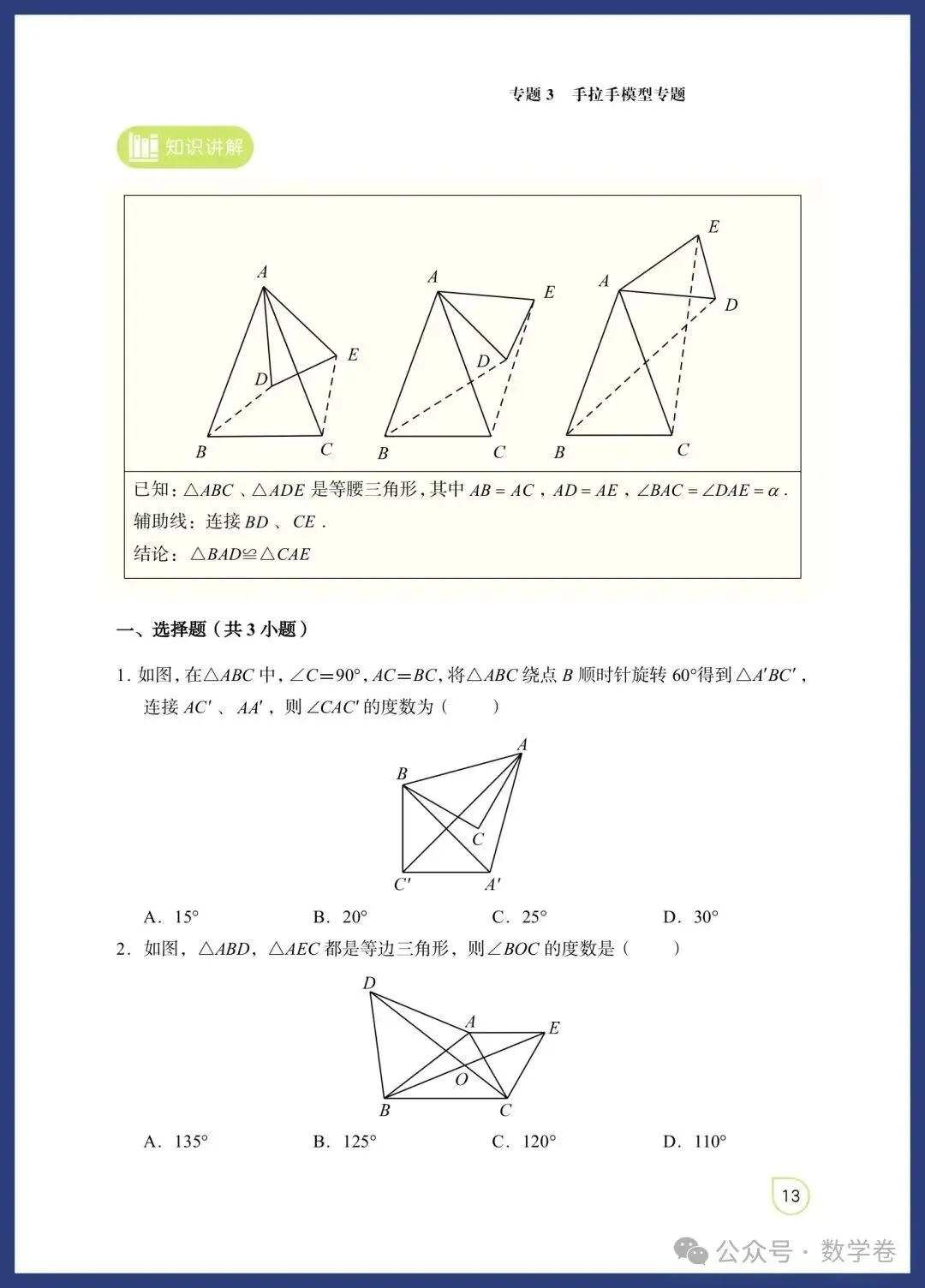
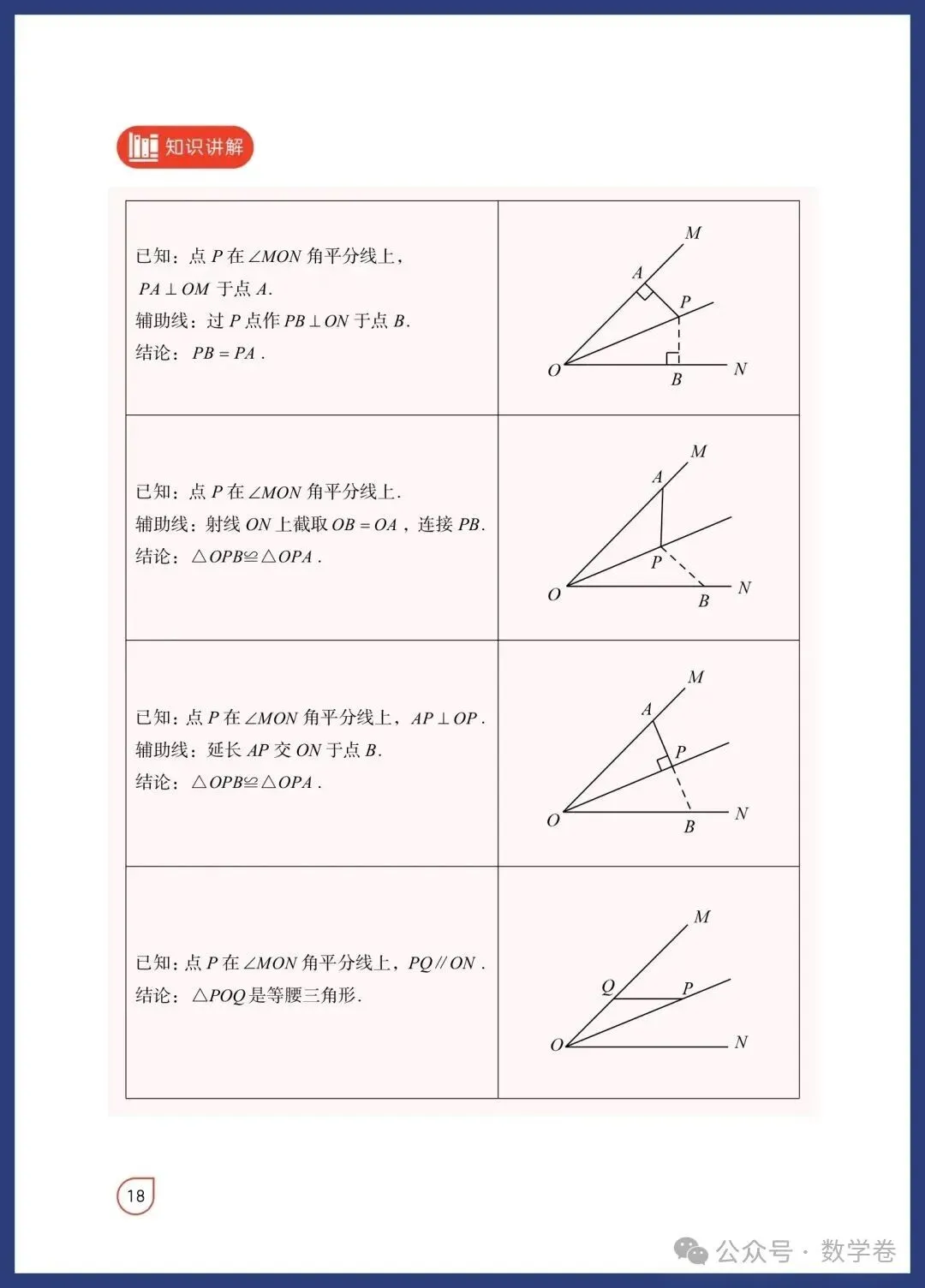
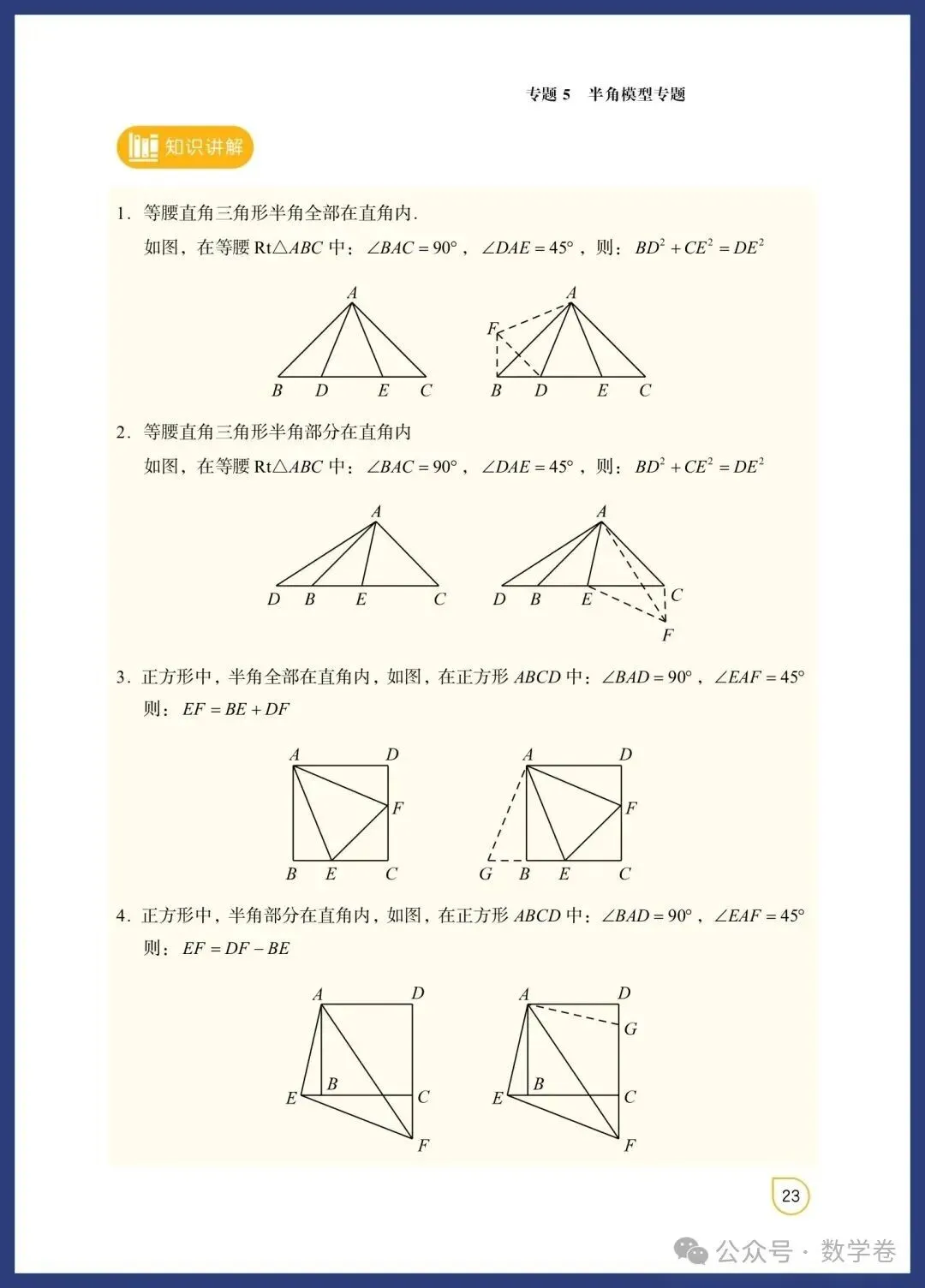
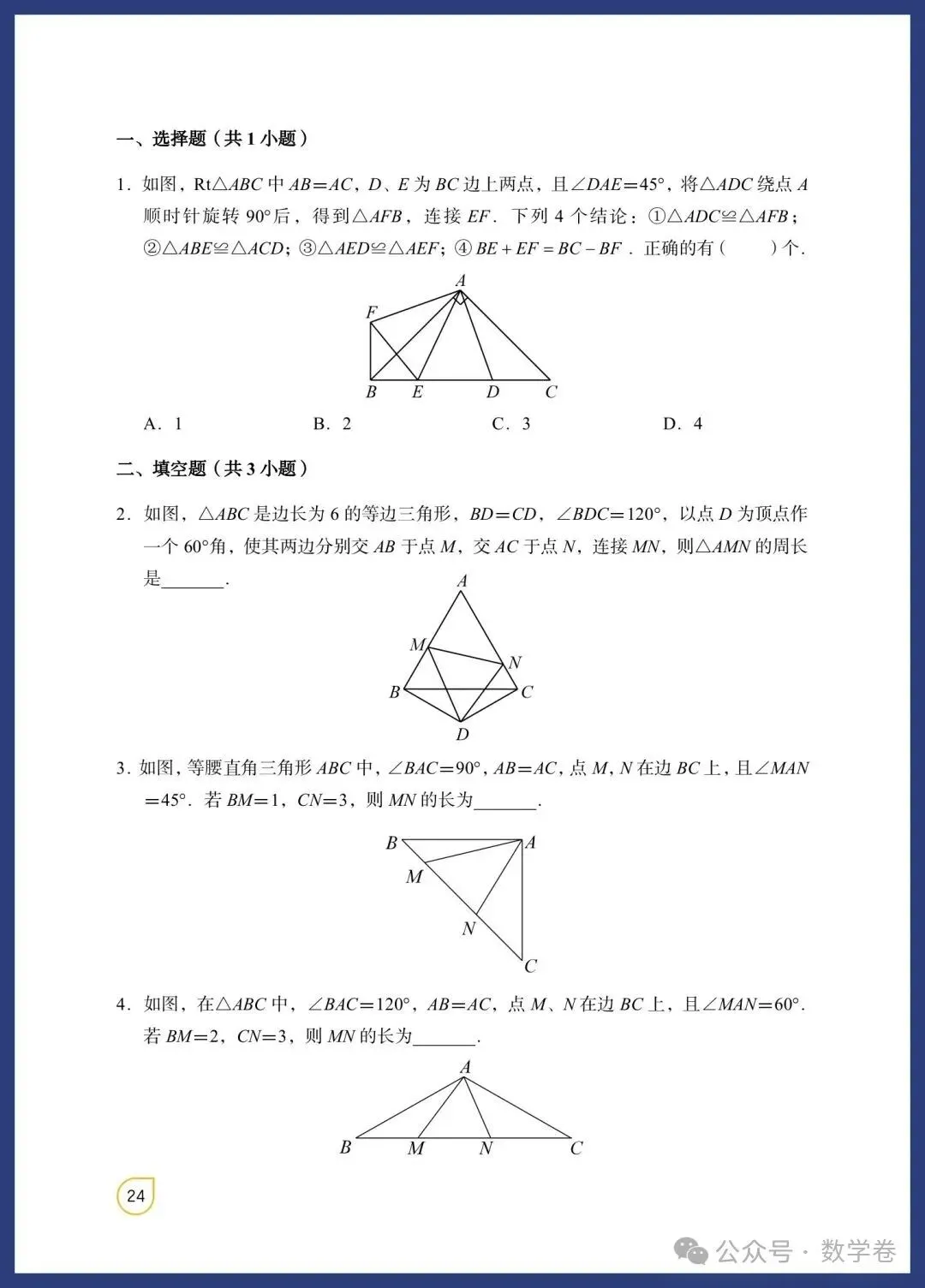
等腰三角形与直角三角形模型融合了特殊三角形的性质与判定，是中考命题的热点。
四边形模型涵盖平行四边形、矩形、菱形、正方形的性质与判定，常与全等、相似结合考查。圆的基本性质模型聚焦弦、弧、角之间的关系，而圆与三角形、四边形的组合模型复杂度更高，需要综合运用多个知识点。
轴对称与中心对称模型帮助理解图形变换，投影与视图模型则培养空间想象能力。
立体图形的展开与折叠模型是连接二维与三维的桥梁，最值问题模型常涉及“将军饮马”等经典题型，而动态几何模型则探究图形在运动变化中的规律。
这些模型不是孤立存在的，在实际考题中常常交叉组合。
建议你在复习时，不仅要记住每个模型的特征和结论，更要多动手画图，理解其证明过程。
通过针对性练习，学会在复杂图形中识别基本模型，化繁为简。系统掌握这12类几何模型，能帮你构建完整的知识网络，面对中考几何题时更加从容自信。
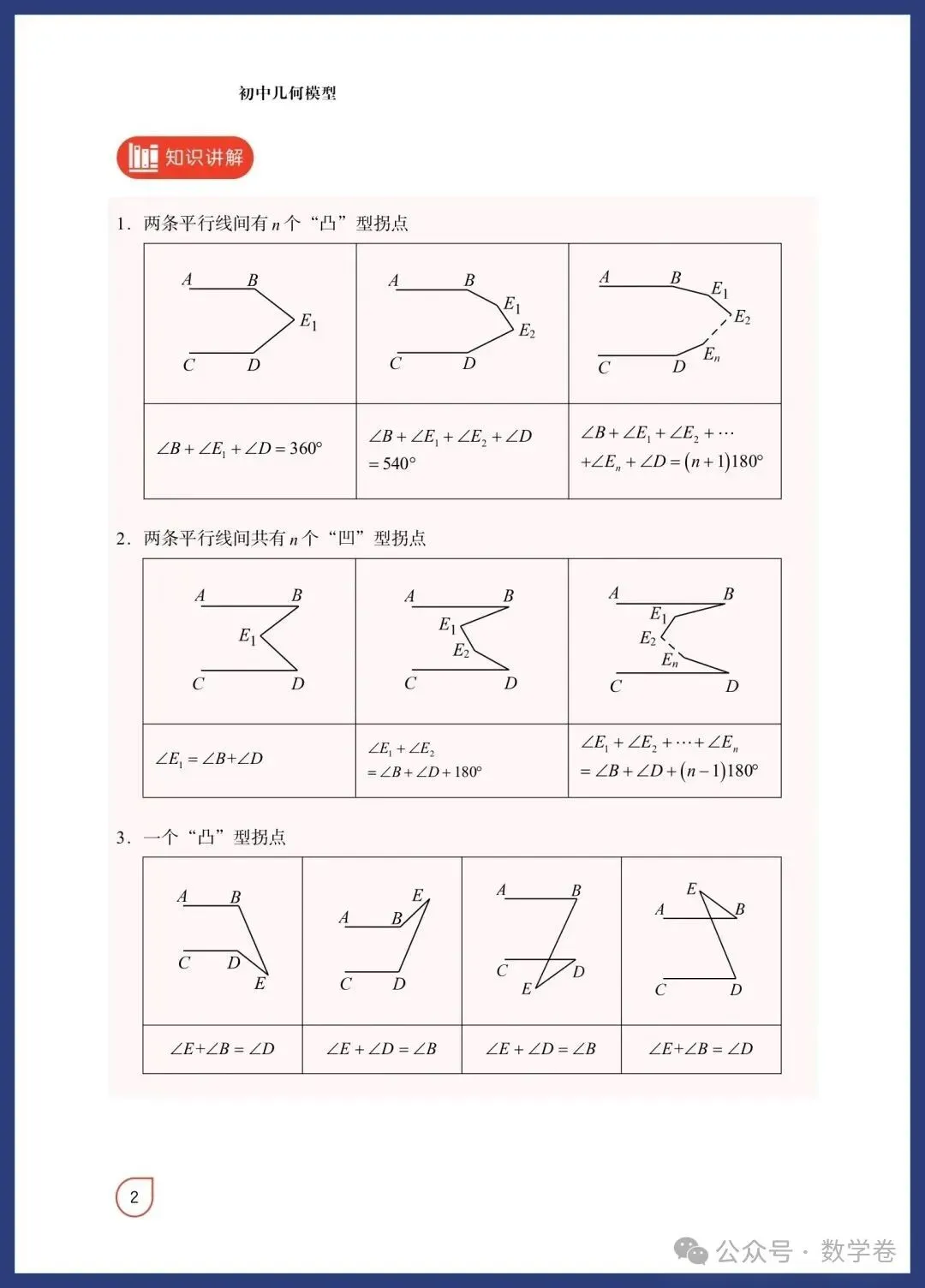
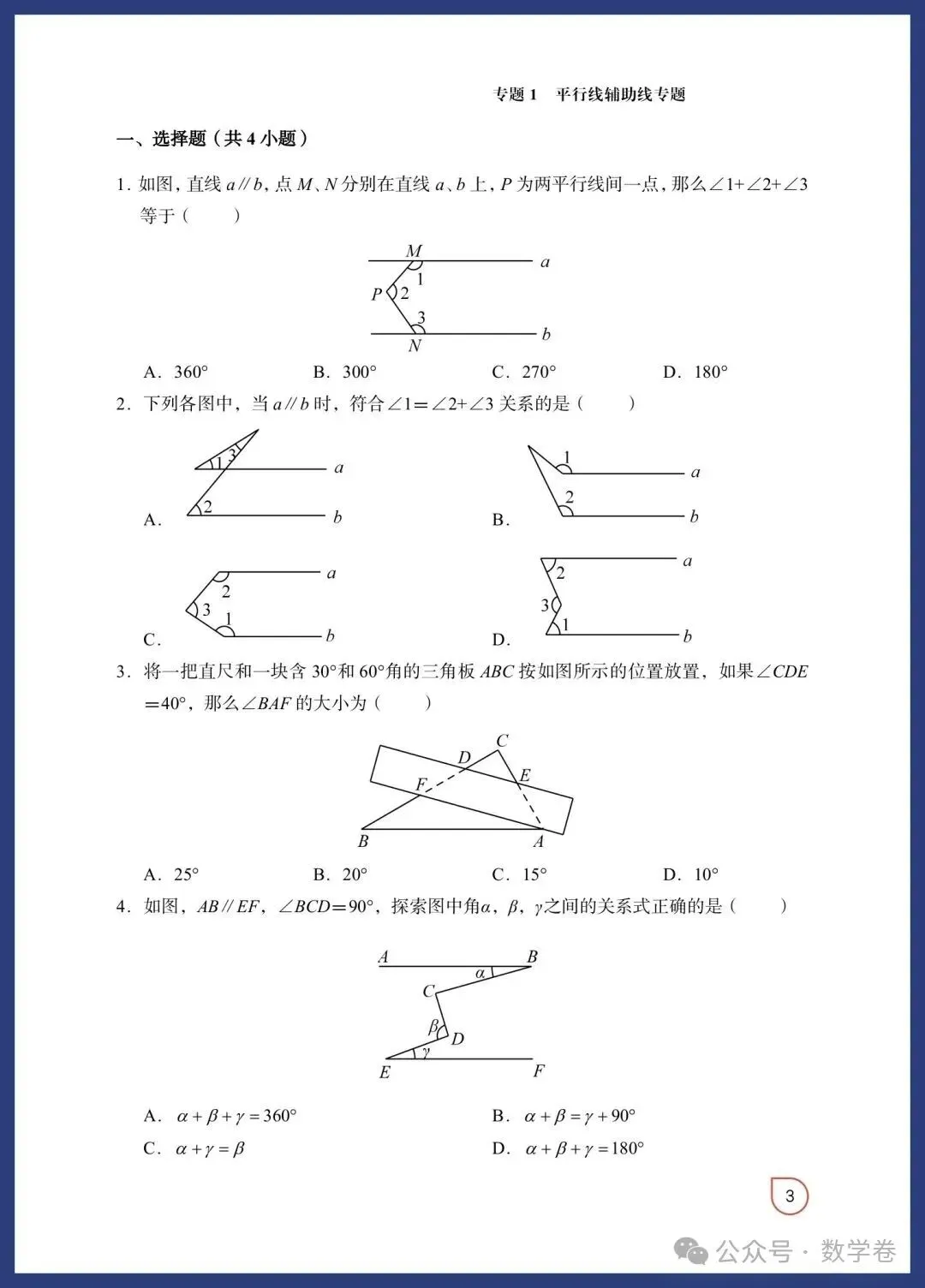
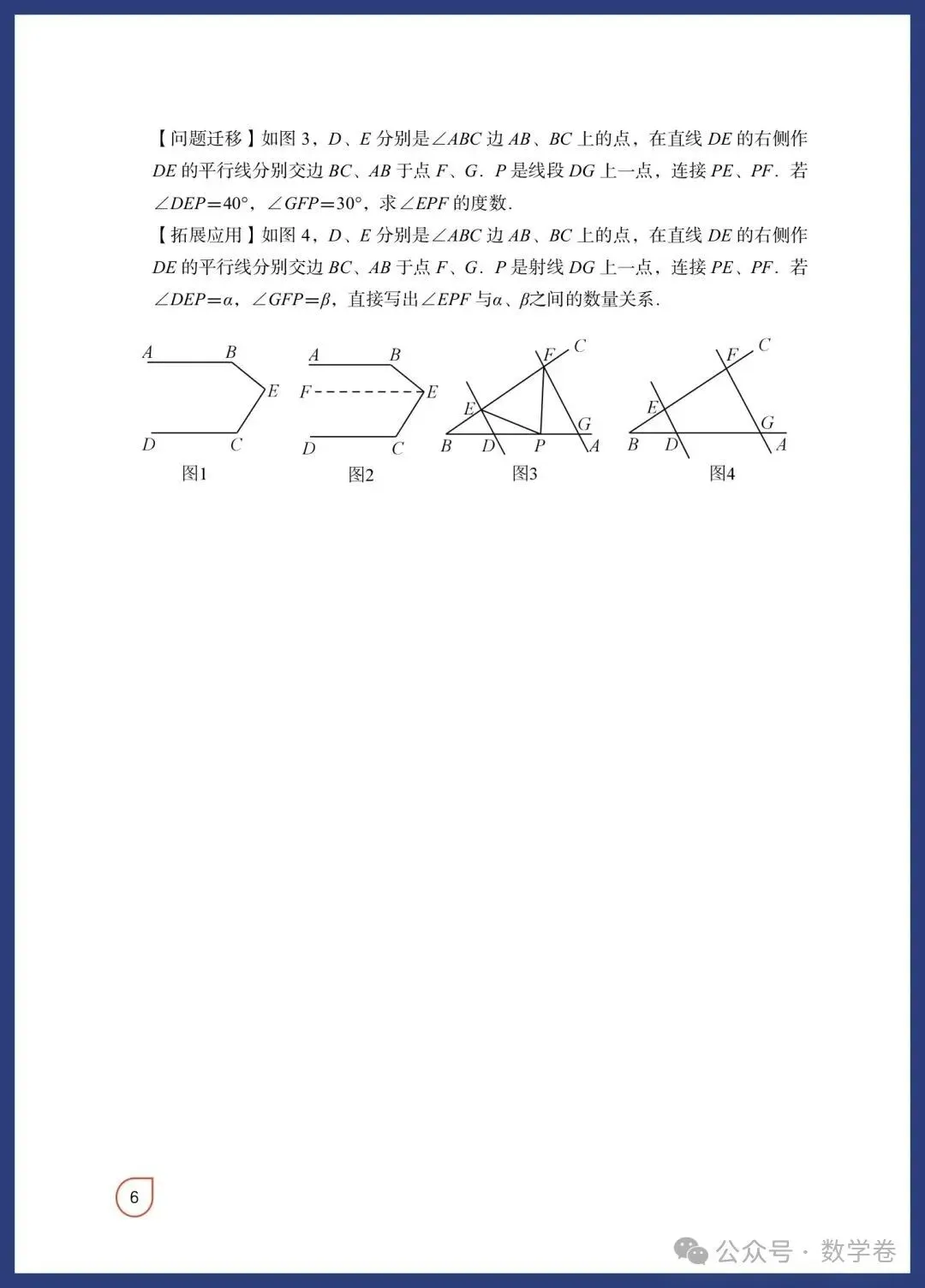
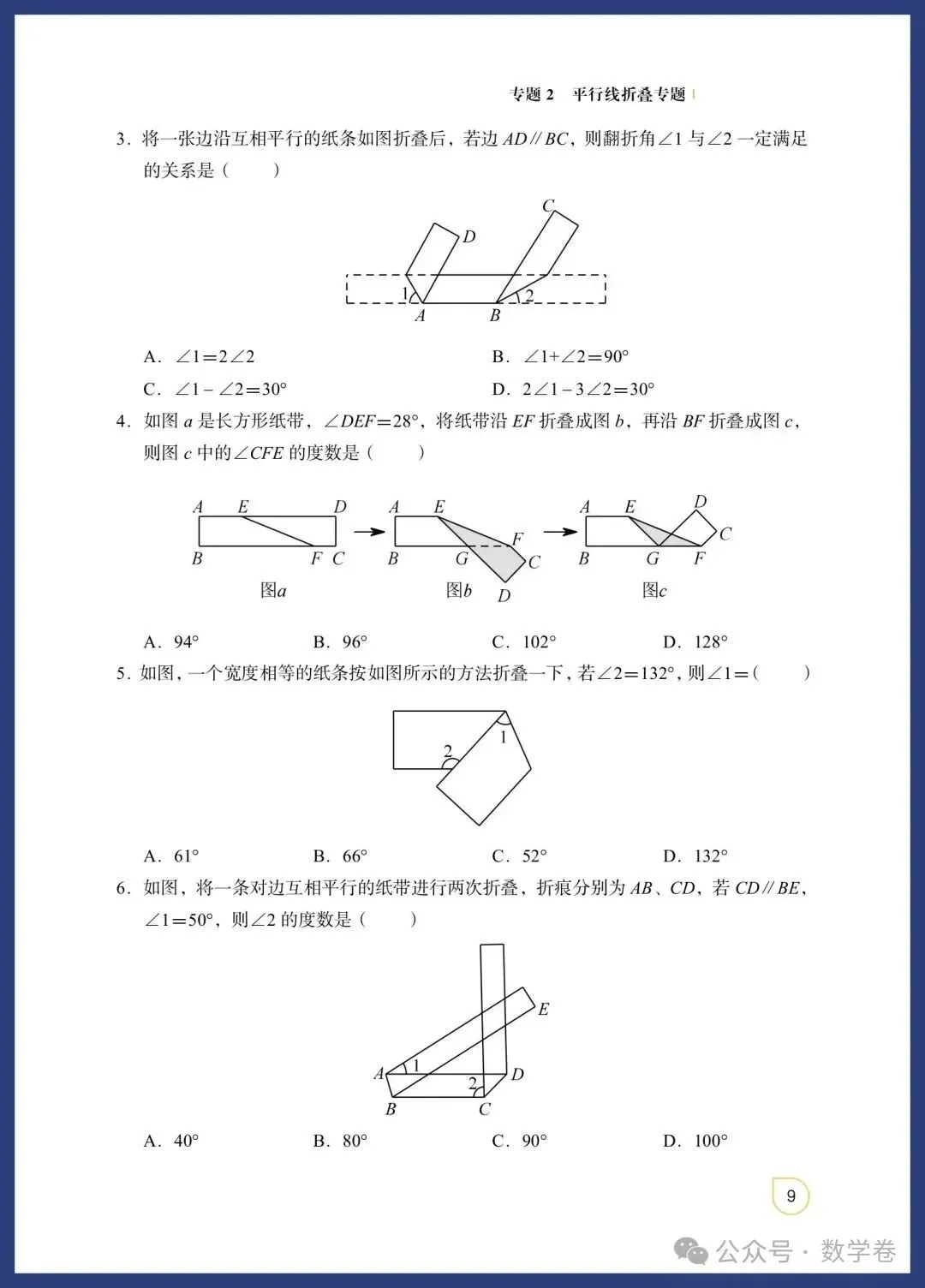
中考数学12个常考模型：
文章来源：
四季读书网
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请发送邮件至23467321@qq.com举报，一经查实，本站将立刻删除;如已特别标注为本站原创文章的，转载时请以链接形式注明文章出处，谢谢！
