中考数学分式计算,掌握这些技巧稳拿分

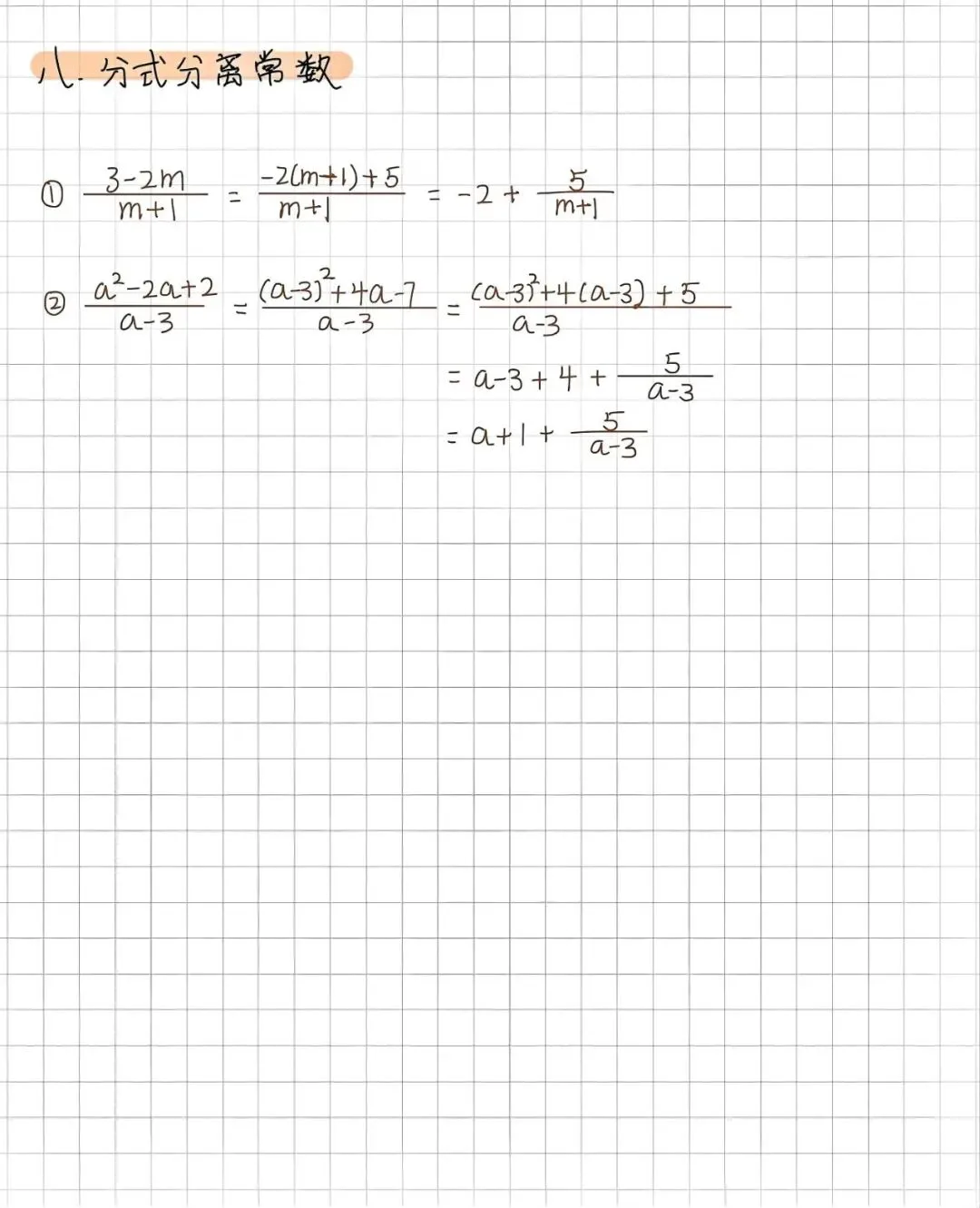
分式计算是中考数学的核心考点，更是代数运算的 “枢纽站”，串联起整式、因式分解、方程等关键知识模块，近年中考对其考查更是做到基础全覆盖，难点则集中在约分通分环节，同时还能考查同学们的符号意识、整体思想和转化能力，想要拿下这部分分数，找对方法很关键。

做分式计算，核心原则是先因式分解再运算，找公因式要取系数最大公因数和相同因式最低次幂，确定最简公分母则要取系数最小公倍数和所有因式最高次幂，约分和通分都要遵循这个规则才不会出错。

分式乘除法要先变除为乘，再交叉约分后相乘；加减法分同分母和异分母，同分母直接分子相加减，异分母先处理符号再通分，混合运算更要注意符号和分子化简，把复杂式子合理变形能让计算更简便。

很多同学失分都在细节上，比如通分时忽略分母的相反数关系，约分时犯局部约分的错误，或是忘记分母不为零的前提。

大家可以建立 “三步检验法”，算完后一验定义域，确保分母不为零；二验运算律，尤其是分配律的使用；三验最简形式，保证分子分母无公因式。

分式求值也有小技巧，切记先化简再求值，遇到比例条件用设 “k” 法，遇到复杂分式可以试试倒数法，条件化简求值则可以先通分再整体代入，这些方法能大幅提高解题效率。

分式计算看似繁琐，实则有章可循，掌握核心方法，做好细节检验，多练多总结，就能轻松攻克这个考点！