(39)2025年杭州市中考
八县区一模数学第24题
已知AB为直径,弦CD⊥AB于E ,作点
B关于CD的对称点H,连结CH并延长
交⊙O于点 P,连结PD.
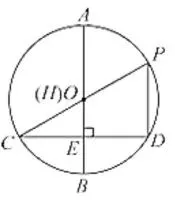
图1
(1)如图1,若对称点H与点O重合,
试求∠CPD的度数,
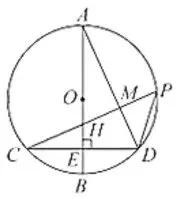
图2
(2)如图2,连结AD交CP于点M,
求证:AD⊥CP ,
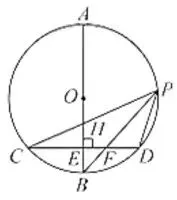
图3
(3)如图3,连结BP交CD于点F,
若AB=3, sin∠CPB=√6/6,
① 试求BE的长;
② 直接写出PC+PD的值.
【解析】(1)∵作点B关于CD的对称点H,
而且对称点H与点O重合,
∴ CD是BH(BO)的垂直平分线,
∴BC=OC ,
∵OC=OB ,
∴OC=OB=BC ,
∴△OBC是等边三角形,
∴∠COB=60° ,
∵AB为直径,
弦CD⊥AB于E ,
∴∠AEC=∠PDC=90°,
∴ AB//PD ,
∴∠CPD=∠COB=60°,
(2)如图4,连接BC, BD,
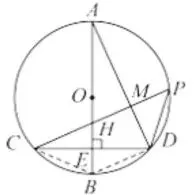
图4
∵ AB⊥CD ,
点B关于CD的对称点H,
∴ HC=CB ,
∠PCD=∠BCD ,
∵AB为直径,
弦CD⊥AB于E ,
∴弧BC=弧BD ,
AD⊥BD ,
∴∠BDC=∠BCD ,
∴∠BDC=∠PCD ,
∴PC//BD ,
∴AD⊥CP,
(3)①如图5,连接AC, BC,
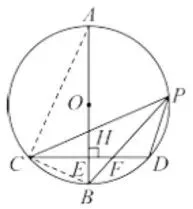
图5
∵∠CAB=∠CPB,
∴sin∠CAB=sin∠CPB
=√6/6,
∴BC=AB·sin∠CAB
=3x√6/6
=√6/2,
∵∠CBE=∠ABC ,
∠ACB=∠CEB ,
∴△ABC∽△CBE ,
∴BC²=BE·BA ,
∴BE=BC²/BA
=(√6/2)²/3
=1/2,
②由⑵得∠PCD=∠BCD ,
弧BC=弧BD ,
HC = CB ,
∴弧PD=弧BD ,
CH=BC=√6/2 ,
∴弧BC=弧PD ,
∴PD=BC=√6/2,
∵1/2BH=BE=1/2
∴BH =1,
∴AH=AB-BH
=3-1
=2,
∵∠BAC=∠BPC ,
∠AHC=∠BHP,
∴△AHC∽△PHB,
∴PH/PH=CH/BH ,
∴2/PH=(√6/2)/1,
∴PH=2√6/3
∴PC+PD=CH+PH+PD
=√6/2+2√6/3+√6/2
=5√6/3 .
往期文章






