

2026
手拉手相似模型
SUBJECT KNOWLEDGE SHARING
初中数学|学科知识分享
< 1 > 模型本质及情景设定
< 2 > 核心条件与结论
< 3 > 模型识别及其应用
< 4 > 总结
< 5 > 配套练习题
坚持做“更有责任心的教育培训机构”
手拉手相似模型
(本质)
手拉手模型是围绕一个公共顶点进行旋转变换的几何构图。它通常涉及两个形状相同的图形,最常见的是三角形。

LIPIN
手拉手相似模型情境设定

· 特殊相似型手拉手核心要点:
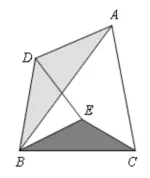
模型特征:如图,在等腰△BAC和等腰△BDE中 ,满足∠ABC=∠DBE,且共顶点B。
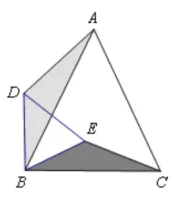
· 一般相似型手拉手核心要点:
模型特征:如图,在△BAC和△BDE中 ,满足∠ABC=∠DBE,且共顶点B。
模型进阶:
· 与“瓜豆原理”(主动点与从动点)联动
手拉手相似模型是理解“瓜豆原理”(种瓜得瓜,种豆得豆)的静态体现。主动点轨迹和从动点轨迹构成的图形,本身就满足手拉手相似关系,这为解决动点路径问题提供了关键思路。
· 与“中点模型”结合
在手拉手模型的基础上,连接对应线段的中点,可以衍生出一系列新的、固定的数量关系和位置关系。
· 与圆、四边形、最值问题融合
模型的变体可以融入圆的性质,或与特殊四边形结合。其旋转特性也常被用来将分散的线段集中,从而利用“两点之间线段最短”解决最值问题。

LIPIN
核心结论与证明思路

结论1:△BAC ∽ △BDE
· 描述:由共顶点引出的两个三角形存在相似关系

结论2:△BEC∽ △BDA
· 描述:根据手拉手相似,可得由同一顶点引出的第二组三角形相似
· 证明思路:
1、由结论1可得△BAC ∽ △BDE,可得BA:BC=BD:BE,且∠ABC=∠DBE
2、所以∠ABC-∠ABE=∠DBE-∠ABE,即∠EBC=∠DBA
3、综上可得:△BEC∽ △BDA

结论3:BE:BD=BC:BA=CE:AD
· 描述:相似三角形对应边成比例,即拉手线长度的比,等于原三角形的相似比
· 证明思路:
1、由结论二:△BEC∽ △BDA
2、根据对应边成比例可得BE:BD=BC:BA=CE:AD

结论4:拉手线AD与EC的夹角,等于原相似三角形的对应夹角(即旋转角,结论证明可参考往期视频号)
LIPIN
模型识别及其应用


1、模型识别:首先从复杂图形中“定位”,当题目图形中出现 “共顶点的两个相似图形” 时,应立刻警觉“手拉手”的可能性。
常见的“信号灯”包括:
(1)共顶点的两个等边三角形或正方形
(2)共顶点且顶角相等的两个等腰三角形。
(3)共顶点的两个直角三角形,且其夹角相等。
2、模型构造:无中生有的“辅助线艺术”
更多时候,题目不会给出完美的手拉手图形,需要我们自己构造,这是解题的难点,也是精髓。
*构造的核心思想:创造一个与已知三角形共顶点且相似的三角形。
3、解题口诀
· 全等型:“两等腰,共顶点,等顶角;连拉手,得全等,角平分。”
· 相似型:“相似形,共顶点;连拉手,成新似;夹角定,比值等。”

LIPIN
总结

“手拉手”模型的学习,不仅仅是记忆几个结论和构图,其终极价值在于领悟 “旋转变换” 这一核心几何思想,掌握从复杂图形中识别基本结构,并通过构造辅助线化未知为已知的能力。它教会我们,许多看似棘手的几何问题,不过是某个基本图形经过旋转、缩放后的样子。当你掌握了这种“动态的眼光”,几何世界将在你眼中变得更加清晰、简洁,也更加美妙。

公众号
附题
接下来看看这道题吧 ⬇️
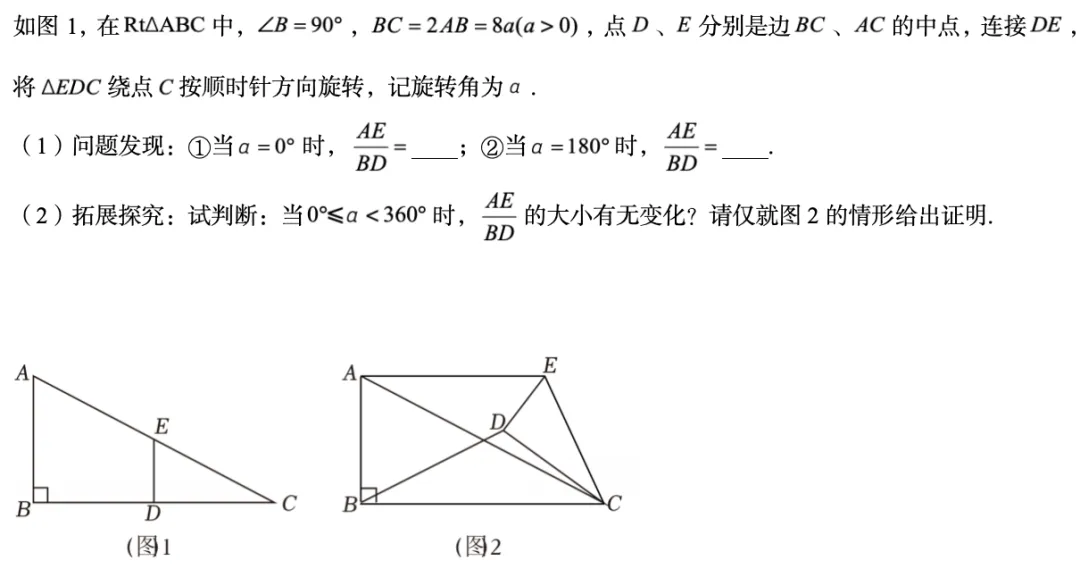
答案放在评论区了~
欢迎大家留言参与讨论 📣

-END-
图文|立品初数组
编辑|立品产品组
审核|立品教学部
更多教育资讯,欢迎关注立品教育~








