
中考数学
2026绵阳中考数学命题趋势分析
基于对绵阳近五年(2021-2025)中考数学真题的剖析,结合2026年命题趋势预测,吴老师认为绵阳中考数学已暂时告别“偏难怪”的题型模式,转而确立了“基础题固本(70%)、中档题提速、压轴题模型化”的稳定格局。2026年命题将呈现“双减”导向下的思维灵活性考查与“跨学科”与“数学文化”深度融合两大特征。压轴题(第24、25题)将很大可能维持“圆与几何综合”与“二次函数与代数几何交汇”的双压轴轮动机制,且对最值问题(胡不归、阿氏圆)与存在性问题(分类讨论)的考查将达到新高度。备考重心应从机械刷题转向核心模型的深度掌握与数学核心素养的培养。
老吴woo
绵阳作为四川省的教育高地,其中考数学命题一直具有鲜明的自主性和前瞻性。在经历了新课标(2022版)的颁布与“双减”政策的深入推进后,绵阳中考数学命题呈现出“稳中求进、变中求新”的总体态势。
从近年来的试卷难度演变来看,呈现出明显的“V型”回调特征。2023年受特定因素影响,试卷难度显著降低,导致高分段考生人数激增。然而,自2024年起,命题导向迅速回调,试卷难度系数回归至正常选拔区间,且区分度更加科学。进入2025年,随着新课标理念的进一步落地,试题在保持整体结构稳定的基础上,更加侧重于考查学生的数学核心素养,如逻辑推理、数学建模及解决实际问题的能力,而非单纯的机械计算。
此外,四川省教育部门已明确未来两三年内暂不实行全省统一命题,各市州将继续自主命题,这为绵阳保持其独特的命题风格提供了政策保障。2026年的命题将在此基础上,进一步强化对学生思维过程、探究能力和创新意识的考查,减少偏题、怪题,增加源于真实情境的开放性与应用性试题。
绵阳中考数学试卷在近五年内保持了极高的结构稳定性,这种稳定性为考生的备考提供了明确的方向。试卷总分150分,题量结构固定为“12+6+7”模式。
试卷由选择题、填空题和解答题三大板块构成。这种结构设计旨在全面覆盖不同层次学生的认知水平,从基础识记到逻辑推理再到综合运用,层层递进。

表格分析:
从表1可以看出,解答题占据了试卷总分的60%,是区分考生数学素养的关键板块。选择题与填空题合计60分,主要起到筛选基础扎实、思维敏捷的考生的作用。特别是填空题的最后两题,往往承担着“小压轴”的角色,其难度甚至不亚于解答题的前一两问。
根据历年真题数据分析,绵阳中考数学试卷的难度梯度控制极为严格,遵循“7:2:1”的黄金法则。
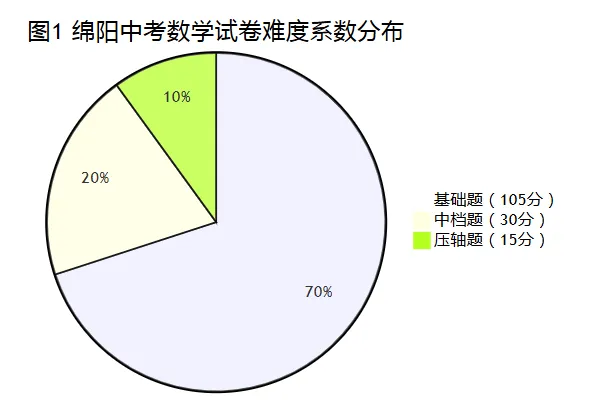
图表分析:
如图1所示,基础题占比高达70%(约105分)。这意味着,对于目标分数在120分左右的中等及以上学生而言,只要能够稳扎稳打,确保基础题与中档题的得分率达到甚至超过95%,就已经奠定了高分的基础。压轴题虽然仅占15%的分值,但由于其极高的思维要求,往往成为拉开尖子生分数差距的“决胜战场”。
在知识点的覆盖上,试卷严格遵循《义务教育数学课程标准》,对数与代数、图形与几何、统计与概率三大领域进行了科学的分值分配。
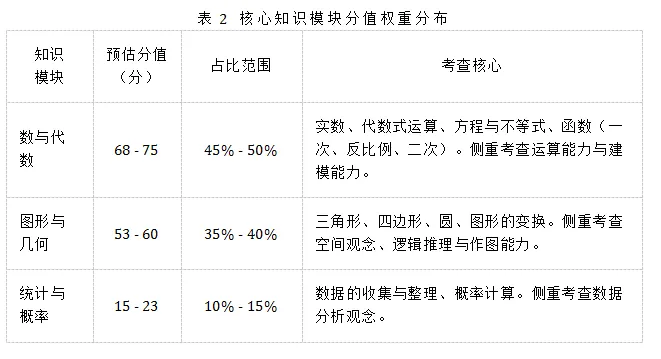
表格分析:
代数与几何是绵阳中考的“半壁江山”,两者合计占比超过85%。值得注意的是,虽然统计与概率分值占比最低,但往往是容易拿分的基础题,不容忽视。在代数模块中,二次函数的综合应用是重中之重;在几何模块中,圆与相似三角形的结合则是高频难点。
通过对近五年真题的拆解,吴老师粗略整理了绵阳中考数学的“考点地图”。以下是对各核心板块高频考点的详细梳理。
一、代数模块:从基础运算到函数综合
代数板块是绵阳中考的基石,考查内容从简单的数与式延伸到复杂的函数综合。
1、数与式(基础送分区):
科学记数法:通常作为第1题或第2题出现,考查大数或小数的表示。
实数运算:涉及相反数、绝对值、平方根等概念,常结合零指数幂考查。
因式分解:以平方差公式和完全平方公式为主,偶尔考查十字相乘法。
分式化简:常结合分式的加减乘除运算,要求考生具备较强的通分与约分能力。
2、方程与不等式(应用建模区):
方程解法:一元一次方程、二元一次方程组、一元二次方程的解法是基本功。
实际应用:
工程问题:如分式方程中的工程效率问题。
行程问题:涉及相遇、追及,常考一元一次方程的应用。
销售利润问题:二元一次方程组的典型应用,考查成本、售价、利润之间的关系。
古代问题:如“鸡兔同笼”,以传统文化为背景考查方程思想。
3、函数(综合压轴区):
一次函数与反比例函数:考查两函数图像的交点问题,结合面积求参数。
二次函数:这是代数部分的巅峰。考查形式包括待定系数法求解析式、顶点坐标、对称轴,以及与几何图形(三角形、四边形)的综合。
二、几何模块:逻辑推理与模型构造
几何板块在绵阳中考中不仅考查记忆,吴老师觉得更侧重于逻辑推理与模型构造。
1、图形的认识与证明:
特殊四边形:平行四边形、矩形、菱形、正方形的判定与性质是必考内容。
三角形:全等三角形(SAS, ASA, AAS, SSS, HL)与相似三角形的判定与性质。
旋转、折叠、对称产生的全等或相似是高频考点。
圆:垂径定理、圆周角定理、切线的判定与性质、弧长与扇形面积计算。
2、动态几何与最值问题:
动点问题:探究线段长度、周长、面积的最值,或探究在运动过程中图形形状的变化。
模型应用:“将军饮马”(对称求最值)、“胡不归”(k·PA+PB型最值)、“阿氏圆”(PA:k·PB型最值)、“瓜豆原理”(路径追踪)等模型在近年压轴题中频繁出现。
三、统计与概率:数据素养的考查
统计:涉及条形统计图、折线统计图、扇形统计图及频数分布直方图的解读。常考查众数、中位数、平均数及方差的计算,并要求利用样本估计总体。
概率:主要考查用列举法(列表格、画树状图)求简单事件的概率,特别是涉及“放回”与“不放回”的情境区分。
压轴题是绵阳中考的“皇冠”,其命题规律具有高度的连续性和逻辑性。通过分析2020-2025年的真题,吴老师发现了一个显著的“双压轴轮动规律”。
绵阳中考数学的最后两道解答题(第24题和第25题)并非每年固定考查某一类知识,而是呈现出“圆与几何综合”和“二次函数与代数几何综合”轮流坐庄的态势。
点击进入:
【绵阳中考数学近五年压轴解答题考察情况汇总(2020-2024)】

表格分析:
从表3可以清晰地看出,“圆”与“二次函数”是压轴题的绝对主角。特别值得注意的是,第25题在近五年中有4次考查的是二次函数综合,而第24题则更多承担了考查“圆”的重任。然而,2022年和2024年也出现了第25题考查四边形或第24题考查圆的特殊情况,这表明命题具有一定的灵活性,但“函数+几何”的双压轴主线不可动摇。
(文后附有2025年全国各地中考数学压轴题解析)。
根据历年真题的高频考点,吴老师将压轴题归纳为以下六大核心题型:
1、存在性问题:这是绵阳压轴题的最爱。主要考查在坐标系中是否存在点P,使得以P为顶点的图形满足特定条件(如等腰三角形、直角三角形、平行四边形、菱形等)。解答此类问题必须进行严谨的分类讨论。
2、定值问题:通常出现在第25题的第(2)或(3)问。要求证明在动点运动过程中,某条线段的长度、线段的比值或某个角的度数始终保持不变。这需要学生具备极强的代数变形能力或几何性质挖掘能力。
3、最值问题:包括几何最值(如垂线段最短、两点之间线段最短)和代数最值(如二次函数顶点最值、配方法求最值)。绵阳中考特别青睐“胡不归”、“阿氏圆”等经典模型的变式考查。
4、面积问题:常结合二次函数,通过割补法或铅垂高法将几何图形的面积用含字母的代数式表示出来,进而求解。
5、阅读理解与新定义:在压轴题的第(1)问中,常会出现“定义一种新运算”或“规定一种新图形”的内容,要求学生现学现用,考查阅读理解与知识迁移能力。
6、分类讨论与数形结合:这不仅是方法,更是贯穿压轴题的灵魂。例如,在研究动点问题时,必须根据动点在不同位置(如在线段AB上、在线段BC上)进行分段讨论。
2026年的绵阳中考数学命题将更加注重对学生核心素养的考查,新题型的出现将成为常态。根据最新的命题趋势,以下三类新题型值得关注。
1、跨学科融合题:物理与数学的碰撞
结合物理知识解决数学问题是绵阳中考的一大特色,这符合新课标中“综合与实践”的要求。
典型模型:杠杆原理与反比例函数。例如,设计一个杠杆模型,动力臂与阻力臂的乘积为定值(阻力×阻力臂为定值),从而得出动力与动力臂成反比例关系。此类题目要求考生能够透过物理现象,抽象出数学模型,列出反比例函数解析式并解决实际问题。
其他融合:可能会涉及光学中的“反射”与几何光学路径(最短路径)的结合,或者运动学中的“v-t图象”与一次函数面积的结合。
2、数学文化与阅读理解题
为了弘扬传统文化并考查学生的阅读理解能力,试题常融入历史元素或新定义。
数学文化:以《九章算术》中的“割圆术”、古代测量问题(如“今有凫起南海”)为背景,考查极限思想或相似三角形的应用。题目通常篇幅较长,要求考生具备快速提取数学信息的能力。
新定义题:例如定义“友好三角形”、“平方点”、“本位数”等新概念,要求考生根据定义进行判断、分类或计算。这类题目旨在考查学生的即学即用能力和逻辑定义的理解深度。
3、 开放性与探究性试题
为了打破标准化答题的固化思维,开放性试题将成为2026年的命题亮点。
条件开放:给出结论,让考生探究前提条件。
结论开放:给出条件,让考生通过观察、猜想得出可能的结论(如“写出图中一个度数为30°的角”)。
解法开放:一道题可能存在多种解法,鼓励学生发散思维,寻找最优解。例如在证明几何结论时,既可以使用全等,也可以使用相似或三角函数。
基于上述分析,针对2026年绵阳中考数学,吴老师建议采取分层备考策略,帮助考生实现精准提分。
备考原则:三轮推进,回归真题
备考应遵循“基础—专题—模拟”的三轮推进模式,但核心在于对近五年(2021-2025)真题的反复研磨。
1、第一轮(地毯式扫盲):
目标:回归课本,构建知识网络。
行动:不放过任何一个概念的定义(如“菱形”与“正方形”的区别),熟背核心公式(如圆幂定理、二次函数顶点坐标公式)。
2、第二轮(模型化专题):
目标:攻克压轴题模型,提升解题效率。
行动:重点突破“胡不归”、“阿氏圆”、“瓜豆原理”、“托勒密定理”在几何最值中的应用;强化二次函数与几何图形(抛物线+四边形)的综合训练。
3、第三轮(实战模拟):
目标:适应考试节奏,规范答题。
行动:每周至少完成一套真题卷(限时120分钟),重点复盘第24题(圆)和第25题(函数)的解题思路,整理错题本。 [10]
针对性提分策略
1、对于基础薄弱(目标100-110分)考生:
(1)死磕选择填空前10题(第1-10题),确保拿到基础分。
(2)解答题前3题(第19-21题)必须满分,特别是统计与概率题,绝对不能失分。
(3)压轴题不强求全做对,争取读懂第1问,哪怕是画图也能得分。
2、对于中等生(目标120-130分)考生:
(1)攻克中档综合题:重点是第22-23题,涉及圆的基础性质或函数的实际应用。
(2)压轴题(第24-25题)的第1-2问:必须通过针对性训练拿下。例如,二次函数压轴题的第一问通常是求解析式,这是送分步骤,必须稳拿。
3、对于尖子生(目标135+分)考生:
(1)死磕“存在性”与“定值”问题:重点训练分类讨论的严谨性和代数运算的准确度。
(2) 关注新题型:多练习跨学科(物理)题目和阅读理解题目,保持思维的灵活性。
(3) 压轴题满分策略:不仅要会做,更要会写。在考试中,当通过特殊位置猜出结论后,必须严格按照逻辑写出严密的证明过程。
心理与应试技巧
1、“跳步”策略:如果一道题思考2-3分钟没有头绪,果断跳过,转战下一道。切忌在一处“卡壳”太久,导致后续简单题没时间做。
2、辅助线意识:在做几何题时,养成“画图”和“加辅助线”的习惯。例如,遇到中点想中位线,遇到角平分线想构造全等,遇到圆想连半径。
3、书写规范:解答题按步骤给分,即使最后结果算错,中间正确的思路和步骤也能获得“过程分”。
综上所述,2026年绵阳中考数学命题将是一场“回归常识”与“素养升级”的综合考量。试卷结构将保持“12+6+7”的稳定形态,难度系数维持在0.7左右。对于广大考生而言,最大的机会在于基础题的稳定性,最大的挑战在于压轴题的模型深度。唯有深刻理解“圆”与“二次函数”这两大核心模块,熟练掌握最值与存在性两大难点题型,并保持对新情境的敏锐适应力,方能在2026年的中考中立于不败之地,实现分数与素养的双重飞跃。

中考数学精品资料
2026中考模拟
2025中考数学压轴题解析
更新中.........
2025中考真题
更新中.........
中考数学最值微课
更新中.........
中考数学知识拓展
更新中.......






