1.(12分)已知抛物线y=ax2+kx+h(a>0).
(1)通过配方可以将其化成顶点式为,根据该抛物线在对称轴两侧从左到右图象的特征,可以判断,当顶点在x轴(填上方或下方),即4ah﹣k2 0(填大于或小于)时,该抛物线与x轴必有两个交点;
(2)若抛物线上存在两点A(x1,y1),B(x2,y2),分布在x轴的两侧,则抛物线顶点必在x轴下方,请你结合A、B两点在抛物线上的可能位置,根据二次函数的性质,对这个结论的正确性给以说明;(为了便于说明,不妨设x1<x2且都不等于顶点的横坐标;另如果需要借助图象辅助说明,可自己画出简单示意图)
(3)利用二次函数(1)(2)结论,证:当a>0,(a+c)(a+b+c)<0时,(b﹣c)2>4a(a+b+c).
(3)构造法之外的常规方法。
1)当a+b+c<0时,左式非负,右式为负,故不等式成立。
2)当a+b+c>0时,则a+c<0,a>0,c<0,a<|c|,b>0。
设d=|c|,则0<a<d,0<a+b-d<b,(b+d)2>4db>4a(a+b-d),即
(b﹣c)2>4a(a+b+c)。

数学思维训练班长期招生(初一到初三,基础班到压轴班)
坐标福州长乐(漳港金峰江田)
详细咨询陈老师13799923966
感谢您帮忙转发和推荐!

答案:【分析】(1)先提公因式a,再利用配方法配成完全平方公式,即可得到答案;
(2)若设x1<x2且不等于顶点横坐标则A,B两点位置可能有以下三种情况:①当A,B都在对称轴左侧时,②当A,B都在对称轴右侧时,③当A,B在对称轴两侧时,根据二次函数性质可得答案;
(3)令y=ax2+(b﹣c)x+(a+b+c),根据点的特殊性得,y=ax2+(b﹣c)x+(a+b+c)上存在两点(﹣1,2a+2c),(0,a+b+c)分别位于x轴两侧,然后根据(1)(2)可得答案.
【解答】解:(1)y=ax2+kx+h=a(x2+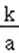 x)+h=a[x
x)+h=a[x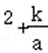 x+(
x+(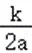 )2﹣(
)2﹣(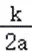 )2]+h=a(x+
)2]+h=a(x+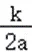 )2﹣
)2﹣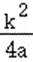 +h=a(x+
+h=a(x+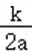 )2+
)2+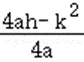 ,
,
∴顶点式为: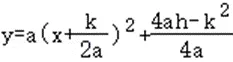 ,当顶点在x轴下方时,即4ah﹣k2<0(填大于或小于)时,该抛物线与x轴必有两个交点;
,当顶点在x轴下方时,即4ah﹣k2<0(填大于或小于)时,该抛物线与x轴必有两个交点;
故答案为: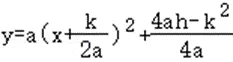 ,下方,<;
,下方,<;
(2)若设x1<x2且不等于顶点横坐标则A,B两点位置可能有以下三种情况:
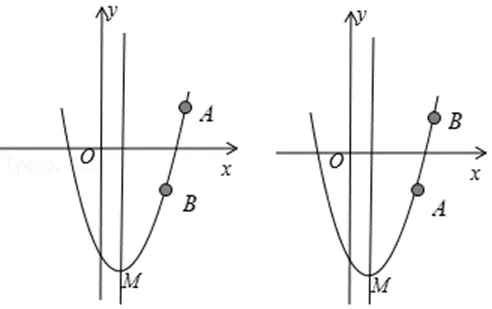
①当A,B都在对称轴左侧时,由于在对称轴左侧,函数值随x的增大而减小,所以点A在x轴上方,点B在x轴下方,顶点M在点B下方,所以抛物线顶点必在x轴下方.如图所示:
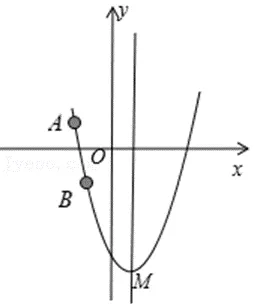
②当A,B都在对称轴右侧时,由于在对称轴右侧,函数值随x的增大而增大,所以点B在x轴上方,点A在x轴下方,顶点M在点A下方,所以抛物线顶点必在x轴下方.如图所示:
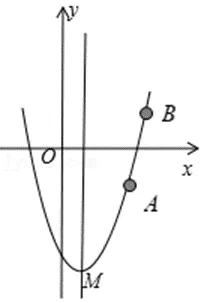
③当A,B在对称轴两侧时,由于A,B分布在x轴两侧,所以不管A,B哪个点在x轴下方,都可以根据抛物线的对称性将其中一个点对称到对称轴另一侧的抛物线上,同①或②,可以说明抛物线顶点必在x轴下方.如图所示:
(3)证明:令y=ax2+(b﹣c)x+(a+b+c),a>0,
当x1=0时,y1=a+b+c;
当x2=﹣1时,y2=2(a+c).
而(a+c)(a+b+c)<0,
∴y1⋅y2<0,
∴y=ax2+(b﹣c)x+(a+b+c)上存在两点(﹣1,2a+2c),(0,a+b+c)分别位于x轴两侧,
∴由(1)(2)可知,y=ax2+(b﹣c)x+(a+b+c)顶点在x轴下方,
即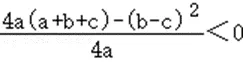 ,
,
又a>0,
∴4a(a+b+c)﹣(b﹣c)2<0,
即:(b﹣c)2>4a(a+b+c).







