
很多小学生做应用题,会一味盯着题目看,不会使用草稿纸草演,更不会画草图梳理题目信息。这是因为学生没有掌握画草图的正确方法,更无法体会画图解决问题的价值。
根据审题的内容画图,把题目的条件、问题在图上表明,借助草图把抽象的数学问题具体化,还原错综复杂信息本来的面目,可以快捷地解决问题,通过画图,也能很快找到自己的错误。
可以说,借助画图解题,是孩子打开解决问题大门的一把“金钥匙”,很多问题都可以迎刃而解。平日教学中,教师可以多演示、多渗透,帮助学生养成画图解题的好习惯。
下面就介绍5种有效的画图方法。
第1种【线段图法】
例:两个小同学折纸鹤,小红折的数量比小丽的3倍还多5个,她俩一共折了53个,问两个人分别折了多少个?
根据题意作图:

解析:看这个线段图,很容易发现53-5,得出的结果再平均分成4份,其中的1份就是小丽折的纸鹤个数。
列式计算:小丽折的个数:(53-5)÷4=12(个),小红折的个数:12 ×3+5=41(个)。
第2种【平面图法】
例1 有两个自然数A和B,如果把A增加12,B不变,积就增加72;如果A不变,B增加12,积就增加120,求原来两数的积。
根据题目的条件比较抽象的特点,不妨借用长方形图,把条件转化为因数与积的关系。先画一个长方形,长表示A,宽表示B,这个长方形的面积就是原来两数的积。如图所示。
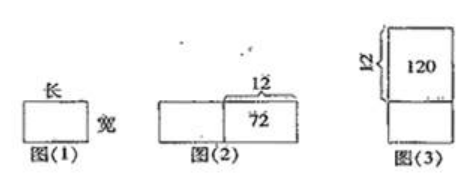
根据条件把A增加12,则长延长12,B不变即宽不变,如图(2);同样A不变即长不变,B增加12,则宽延长12,如图(3)。从图中不难找出:
原长方形的长(A)是120÷12=10
原长方形的宽(B)是72÷12=6
则两数的积为10×6=60
借助长方形图,弄清了题中的条件,找到了解题的关键。
第3种【立体图法】
例:把一个正方体切成两个长方体,表面积就增加了8平方米。原来正方体的表面积是多少平方米?
根据题意作图:
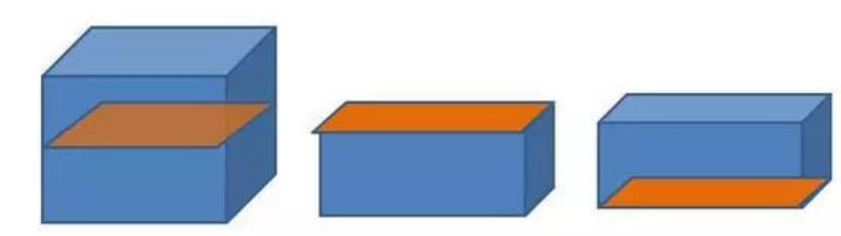
解析:由图可知,增加的8平方米,就是正方体的2个面,每个面的面积是8÷2=4(平方米),则正方体的表面积是:4×6=24(平方米)。
第4种【列表图法】
例:有一个5分币,4个2分币,8个1分币。要拿9分钱,有几种拿法?
根据题意作图:
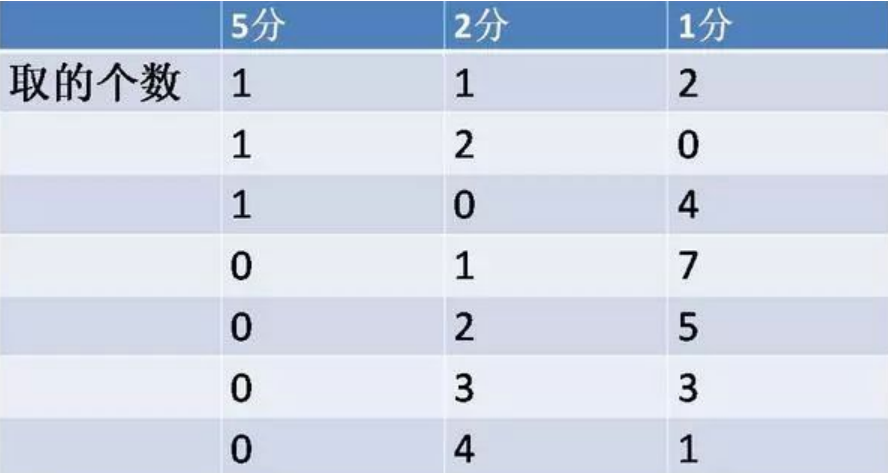
由列表图,可以清楚看到共有7种拿法。
第5种【树状图法】
例:小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清就随便穿了两只。小明正好穿的是同一双袜子的可能性是多少?
解析:假设2双袜子为A袜、B袜,那么4只袜子分别是A1、A2、B1、B2,根据题意作图:
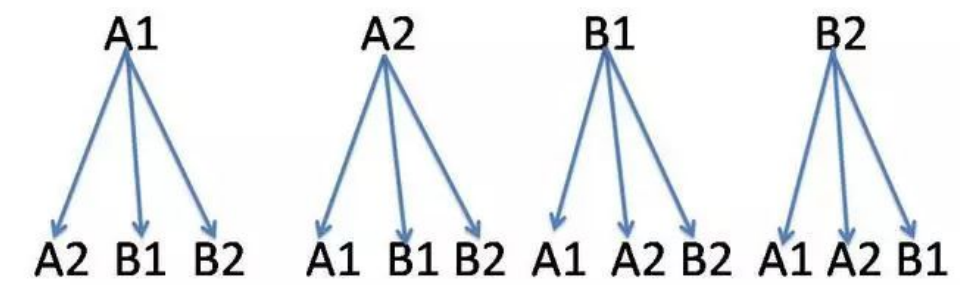
由树状图可知,2双袜子任意搭配有12种情况,其中同一双的情况有4种,所以小明穿同一双袜子的的可能性是4/12,也就是1/3。
中小学生必读名著在线听书MP3合集







