2024年安徽省六安市名校联考中考数学模拟试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)下列各数中,最大的数是( )
A.﹣4 B.0 C.1 D.﹣2024
【解答】解:∵﹣2024<﹣4<0<1,
∴最大的数是:1.
故选:C.
2.(4分)下列算式中,计算结果为4m4的是( )
A.6m2﹣2m2 B.4m2•m2 C.m5÷4m D.(﹣4m2)2
【解答】解:A、6m2﹣2m2=4m2,故本选项不符合题意;
B、4m2•m2=4m4,故本选项符合题意;
C、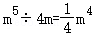 ,故本选项不符合题意;
,故本选项不符合题意;
D、(﹣4m2)2=16m4,故本选项不符合题意;
故选:B.
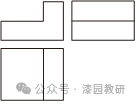
3.(4分)某几何体的三视图如图所示,则该几何体为( )
A.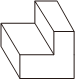 B.
B.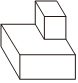 C.
C.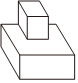 D.
D.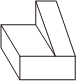
【解答】解:根据三视图的形状,结合三视图的定义以及几何体的形状特征可得该几何体为A选项.
故选:A.
4.(4分)下列函数的图象与y轴正半轴有交点的是( )
A.y=﹣3x﹣3 B.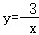 C.y=2x2﹣1 D.y=(x﹣2)2
C.y=2x2﹣1 D.y=(x﹣2)2
【解答】解:A、当x=0时,y=﹣3,与y轴交点在负半轴上,不符合题意;
B、由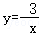 的图象与x,y轴无交点,不符合题意;
的图象与x,y轴无交点,不符合题意;
C、当x=0时,y=﹣1,与y轴交点在负半轴上,不符合题意;
D、当x=0时,y=4,与y轴正半轴有交点,符合题意.
故选:D.
5.(4分)如图,AB∥CD,点E是CD上一点,EF⊥AC于点F,若∠CEF=25°,则∠A的度数为( )
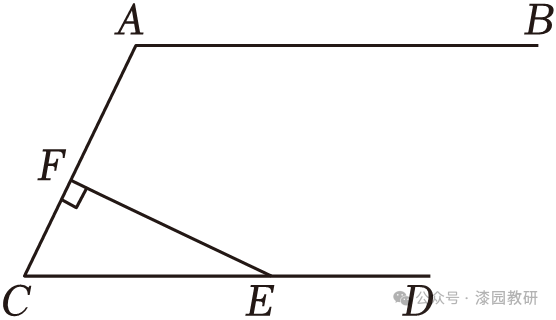
A.105° B.110° C.115° D.120°
【解答】解:∵EF⊥AC,
∴∠CFE=90°,
∵∠CEF=25°,
∴∠C=180°﹣∠CFE﹣∠CEF=65°,
∵AB∥CD,
∴∠C+∠A=180°
∴∠C=180°﹣∠A=115°
故选:C.
6.(4分)如图是甲、乙两人手中的扑克牌,两人随机出一张牌,记甲、乙牌中的数分别为m,n,使得﹣2≤m﹣n≤2的概率为( )
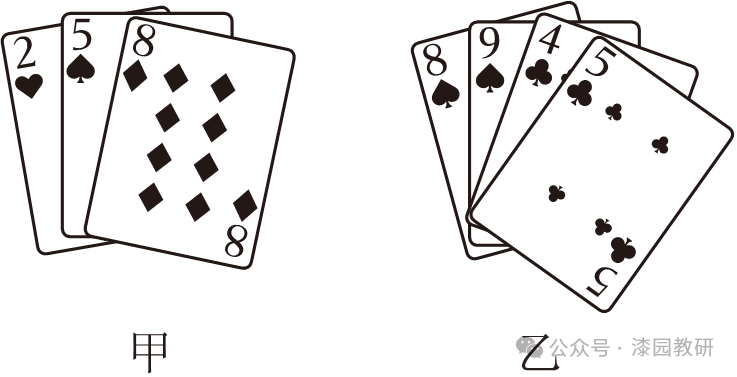
A.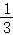 B.
B.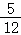 C.
C.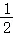 D.
D.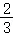
【解答】解:树状图如下:
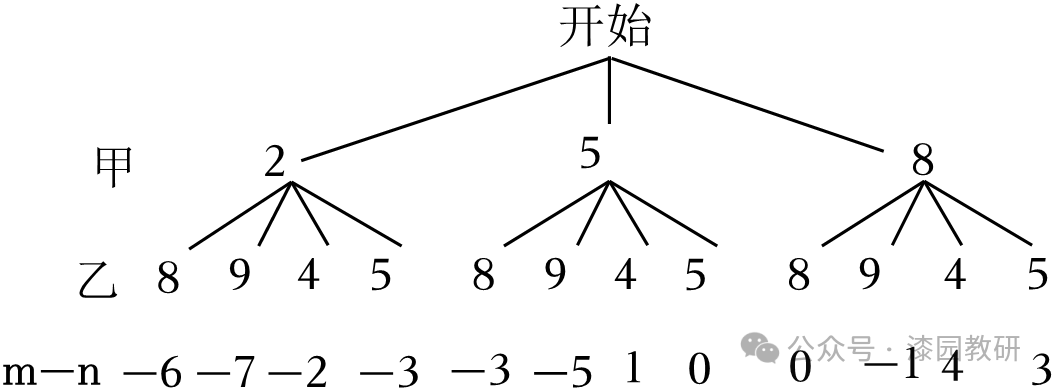
所有可能的结果有12种,甲获胜的情况有5种,
∴甲获胜的概率都是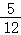
故选:B.
7.(4分)如图,在半径为5的⊙O中,弦AB与弦CD互相垂直,垂足为点E,如果AB=CD=8,那么OE的长为( )
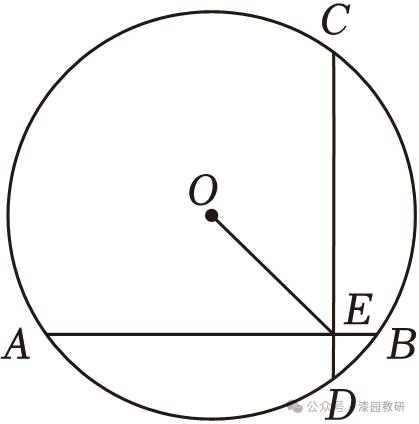
A.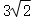 B.3 C.4 D.
B.3 C.4 D.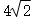
【解答】解:如图,连接OC,OA,过O作OH⊥AB于H,过O作OQ⊥CD于Q,
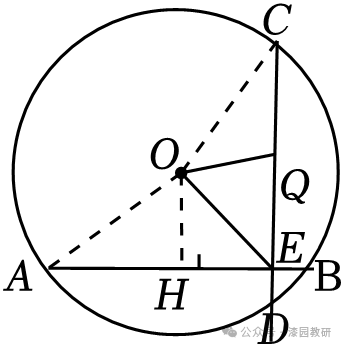
∵AB=CD=8,
∴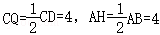
∵OC=OA=5,
∴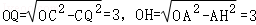
∴OQ=OH,
∴AB⊥CD,OQ⊥CD,OH⊥AB,
∴四边形OQEH是正方形,
∴OH=EH=3,
∴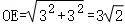 .
.
故选:A.
8.(4分)某工厂计划用两年时间使产值增加到目前的4倍,并且使第二年增长率是第一年增长率的2倍,设第一年增长率为x,则可列方程得( )
A.(1+x)2=4 B.x(1+2x+4x)=4
C.2x(1+x)=4 D.(1+x)(1+2x)=4
【解答】解:∵第二年增长率是第一年增长率的2倍,且第一年增长率为x,
∴第二年增长率为2x.
设该工厂原产值为a,则两年后产值为4a,
根据题意得:a(1+x)(1+2x)=4a,
即(1+x)(1+2x)=4.
故选:D.
9.(4分)函数y=ax2+bx(a≠0)与y=ax+b的图象可能是( )
A.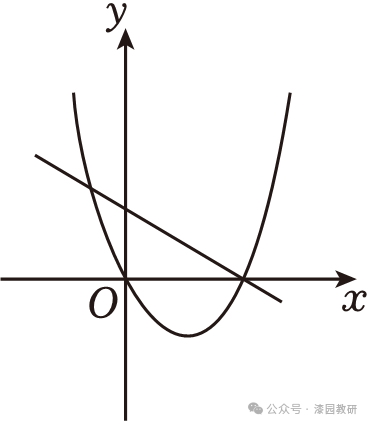 B.
B.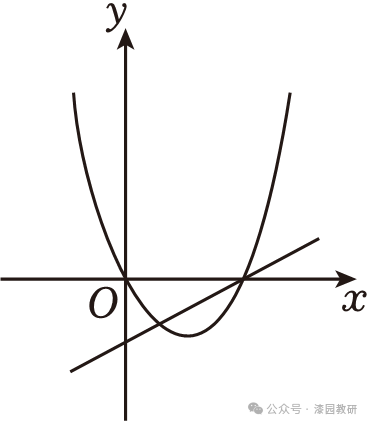
C.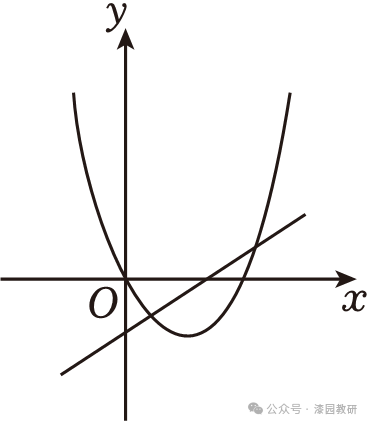 D.
D.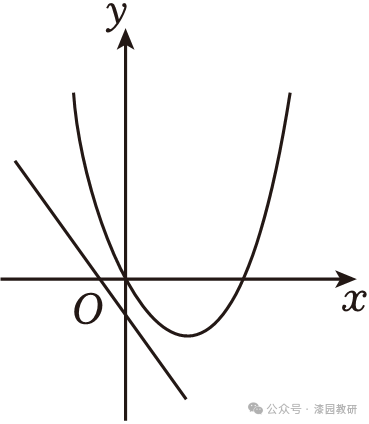
【解答】解:由四个选项可知,二次函数开口均向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该经过第一、三、四象限,
当ax2+bx=0时,即x1=0,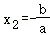
当ax+b=0时,即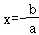
则二次函数与一次函数在x轴上有一交点,且为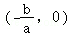
A.一次函数图象经过第一、二、四象限,故本选项不符合题意.
B.一次函数图象经过第一、三、四象限,且有一交点在x轴上,故本选项符合题意.
C.一次函数图象经过第一、三、四象限,但交点均不在x轴上,故本选项不符合题意.
D.一次函数图象经过第二、三、四象限,故本选项不符合题意.
故选:B.
10.(4分)在△ABC中,AH是BC边上的高,CD是AB边上的中线,CH=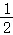 AB.若AB=10,AH=6,则tan∠DCH的值为( )
AB.若AB=10,AH=6,则tan∠DCH的值为( )
A.2或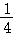 B.2或
B.2或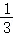 C.3或
C.3或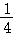 D.3或
D.3或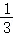
【解答】解:如图1,当H在BC上时,作DE⊥BC,垂足为E,
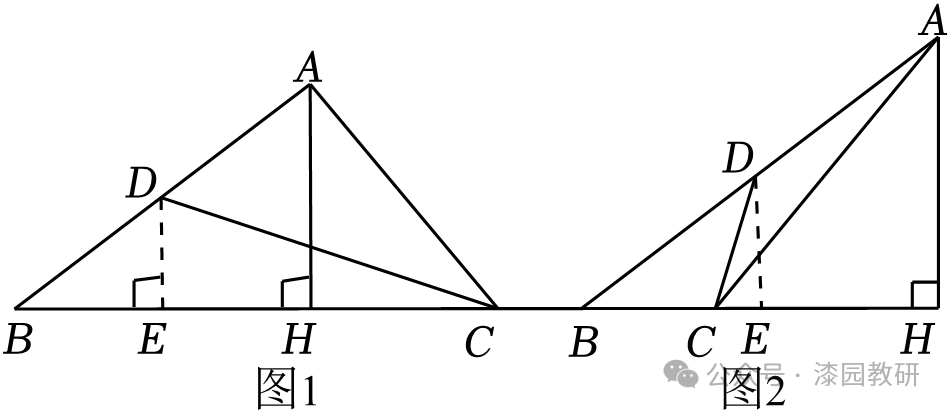
∵AB=10,AH=6,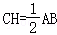
∴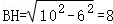 =5.
=5.
∵CD是AB边上的中线,
∴BD=AD,
∵AH是BC边上的高,
∴DE∥AH,
∴△BDE∽△BAH,
∴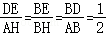 .
.
∴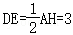
故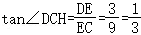 ;
;
如图2,当H在BC的延长线上时,同理可得可得,
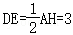
故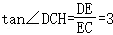 .
.
故选:D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)2023年合肥常住人口达到985.3万人,“985.3万”用科学记数法表示为 9.853×106 .
【解答】解:985.3万=9853000=9.853×106.
故答案为:9.853×106.
12.(5分)若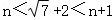 ,则整数n的值是 4 .
,则整数n的值是 4 .
【解答】解:∵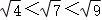
∴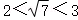
∴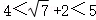 .
.
∵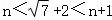
∴n=4.
故答案为:4.
13.(5分)如图,四边形ABCD内接于⊙O,PA,PC与⊙O分别相切于A,C,若∠D=70°,则∠P+∠B= 150 °.
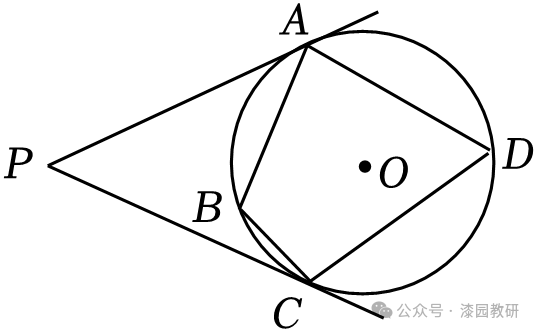
【解答】解:连接OA,OC,
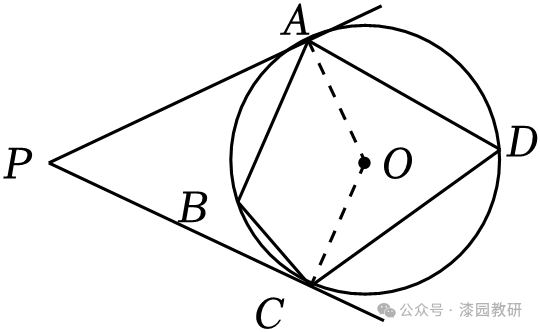
∵四边形ABCD内接于⊙O,
∴∠ABC=180°﹣∠D=180°﹣70°=110°,
由圆周角定理得,∠AOC=2∠D=140°,
∵PA,PC与⊙O分别相切于A,C,
∴∠PAO=∠PCO=90°,
∵∠P+∠PAO+∠PCO+∠AOC=360°,
∴∠P=360°﹣90°﹣90°﹣140°=40°,
∴∠P+∠B=40°+110°=150°,
故答案为:150.
14.(5分)如图,在菱形ABCD中,点P是AD上一点,将△ABP沿着BP折叠,得到△EBP,连接CE.
(1)若∠ABC=130°,∠ABP=16°,则∠BCE的度数为 41 °;
(2)点Q是CE的中点,若∠A=60°,AB=4,则DQ的最小值为 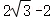 .
.
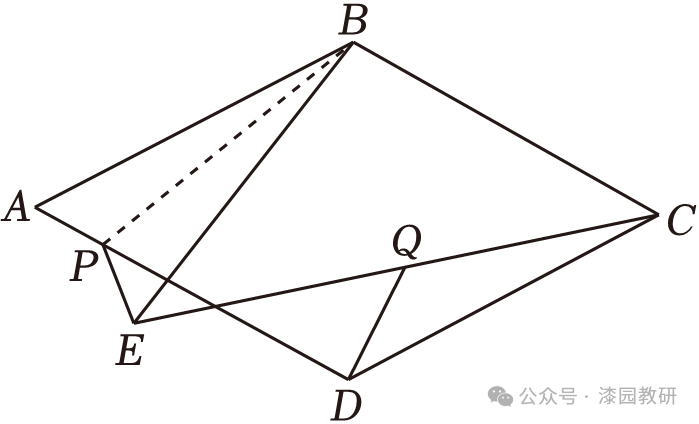
【解答】解:(1)由折叠和菱形的定义可知,AB=BE=BC,∠ABE=2∠ABP=32°,
则∠CBE=∠ABC﹣∠ABE=98°,
∴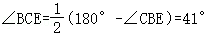
故答案为:41;
(2)延长CD至点F,使得CD=DF,连接BF,EF,
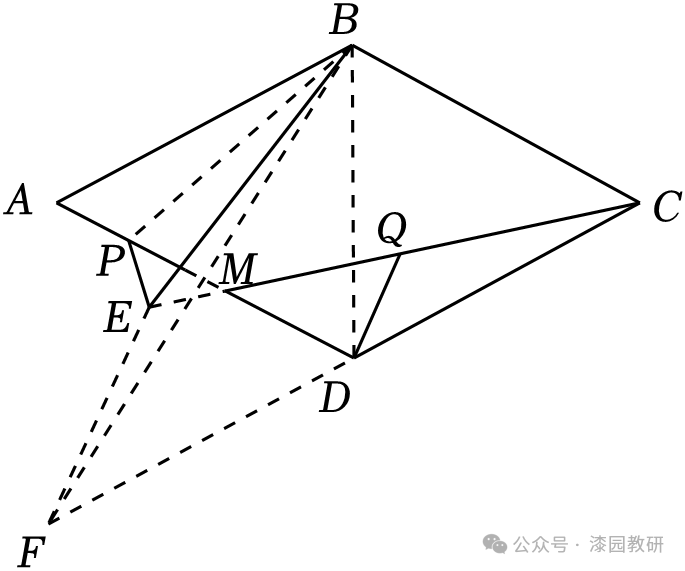
则DQ是△CEF的中位线,
∴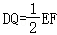
当EF取最小值时,DQ有最小值.
连接BD,
∵四边形ABCD是菱形,
∴AB=AD=CD=BC=4,AD∥BC,
又∠A=60°,
∴△ABD是等边三角形,
则DF=BD=CD=4,∠BCF=∠A=60°,
∴∠ADF=∠BCF=60°,
∴AD⊥BF,垂足为M,
∴∠F=30°,BF=2CF,
∴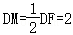
∴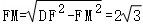
∴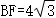 .
.
由折叠可知BE=BA=4,
又BE+EF≥BF,
∴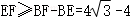
当点B,E,F共线时,EF有最小值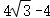
此时DQ的最小值为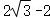
故答案为: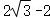 .
.
三、(本大题共2消息,每小题8分,满分90分)
15.(8分)解不等式: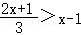 .
.
【解答】解: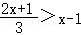
2x+1>3(x﹣1),
2x+1>3x﹣3,
﹣x>﹣4,
x<4.
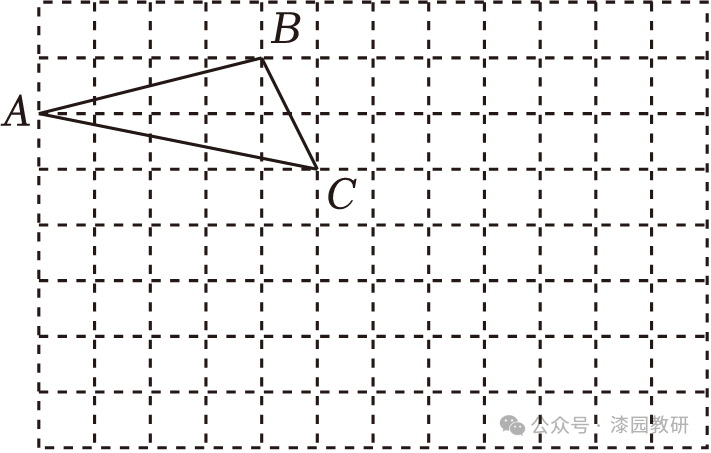
16.(8分)如图,在由边长为1个单位长度的小正方形组成的网格中,已知△ABC的顶点都在网格上,完成下列任务.
(1)将△ABC向右平移4个单位长度,再向下平移4个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)以点C1为旋转中心,将(1)中△A1B1C1按顺时针方向旋转90°,得到△A2B2C1,画出△A2B2C1;
(3)在(1)(2)的条件下,利用网格点和无刻度的直尺画出线段A2C1的中点P.
【解答】解:(1)△A1B1C1如图所示;
(2)△A2B2C1如图所示;
(3)点P如图所示.
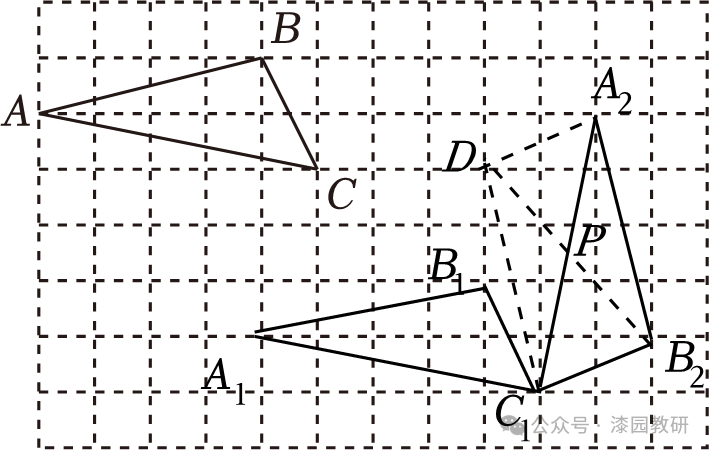
∵A2D∥B2C1,A2B2∥C1D,
∴四边形A2B2C1D为平行四边形,
∴A2P=C1P,
∴P为线段A2C1的中点.
17.(8分)我国古代数学著作《张丘建算经》中著名的“百鸡问题”叙述如下:“鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?”意思是公鸡五钱一只,母鸡三钱一只,小鸡一钱三只,要用一百钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?若现已知小鸡买78只,求公鸡、母鸡各买几只.
【解答】解:设公鸡买x只,母鸡买y只,
依题意,得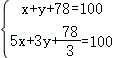
解得: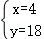
答:公鸡买4只,母鸡买18只.
18.(8分)观察下列等式:
第1个等式: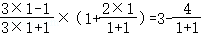 ;
;
第2个等式: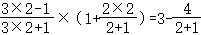 ;
;
第3个等式: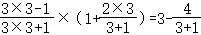 ;
;
第4个等式: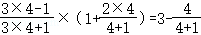 ;
;
……
按照以上规律,解答下列问题:
(1)写出第5个等式: 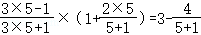 ;
;
(2)写出你猜想的第n个等式: 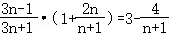 (用含n的等式表示),并证明.
(用含n的等式表示),并证明.
【解答】解:(1)第5个等式: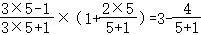 ;
;
(2)第n个等式: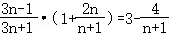 ;
;
证明如下:
等式左边=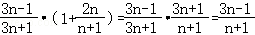
等式右边=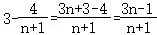
∴左边=右边,
∴等式成立.
19.(10分)某数学兴趣小组测量太湖山国家森林公园内望江塔AB的高度,如图,已知望江塔AB与水平地面BC垂直,望江塔AB与斜坡CD之间的距离BC长为14米,测得斜坡CD的坡度i=5:12,斜坡CD长为6.5米,坡顶D处有一个测角仪DE,DE⊥BC,从点E测得塔顶点A的仰角为38.8°,已知测角仪DE长为1.5米,求望江塔AB的高度.(精确到1米,图中所有点都在同一平面,参考数据:sin38.8°≈0.63,cos38.8°≈0.78,tan38.8°≈0.80)
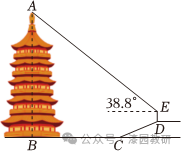
【解答】解:如图,过点E作EG⊥AB干点G,延长ED交BC于点H,则四边形EGBH是矩形,
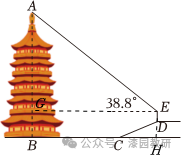
∴BG=EH,EG=BH.
在中,由斜坡CD的坡度i=5:12,
设DH=5x,则CH=12x,
∴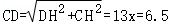 米,
米,
解得:x=0.5,
∴DH=2.5米,CH=6米.
∴EG=BH=BC+CH=14+6=20米,BG=EH=DE+DH=1.5+2.5=4米.
在Rt△AEG中,AG=EG×tan∠AEG=20×tan38.8°≈20×0.80=16米.
∴AB=AG+BG=16+4=20米.
答:望江塔AB的高度约为20米.
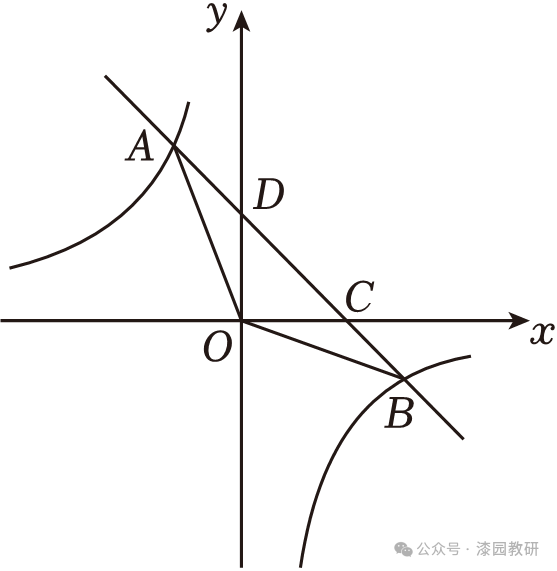
20.(10分)如图,在平面直角坐标系xOy中,直线y=ax+4与反比例函数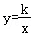 的图象交于A(﹣2,m)、B两点,与x轴交于点C(4,0),与y轴交于点D.
的图象交于A(﹣2,m)、B两点,与x轴交于点C(4,0),与y轴交于点D.
(1)求a,k的值;
(2)求△AOB的面积;
(3)根据图象,直接写出反比例函数值小于一次函数值时x的取值范围.
【解答】解:(1)把C(4,0)代入y=ax+4,得:
0=4a+4,
∴a=﹣1.
把A(﹣2,m)代入y=﹣x+4,得:
m=﹣(﹣2)+4=6,
把A(﹣2,6)代入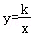 ,得:
,得:
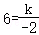
∴k=﹣12;
(2)当x=0时,y=﹣0+4=4,
∴D(0,4).
解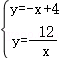 得
得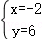 或
或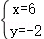
∴B(6,﹣2),
∴S△AOB=S△AOD+S△DOB
=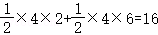 ;
;
(3)由图象可知,当反比例函数值小于一次函数值时x的取值范围是x<﹣2或0<x<6.
21.(12分)某学校组织开展主题为“节约用水,共建绿色校园”的社会实践活动.在关于节约用水知识测试中,随机在七年级和八年级分别抽取20名同学进行相关知识测试,统计他们的测试成绩(x),并绘制相关统计图(不完整),请你根据以下相关信息完成下列任务.
信息1
七年级成绩:84,78,98,92,98,92,69,92,89,89,85,84,83,79,92,79,83,78,92,58.
信息2
八年级成绩在80≤x<90之间的数据为:89,88,85,81.
信息3
七年级抽取同学的成绩频数分布直方图和八年级抽取同学的成绩频数分布扇形统计图如下:
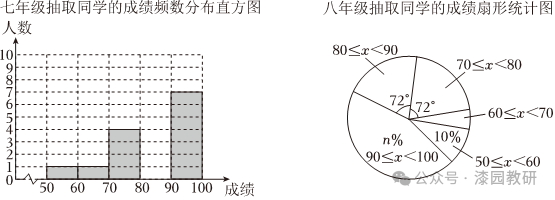
(1)填空:n= 45 ,并补全七年级抽取同学的成绩频数分布直方图;
(2)请你补全七年级和八年级抽取同学的成绩数据的特征表:
| 平均数 | 众数 | 中位数 | 方差 |
七年级 | 84.7 | 92 | 84.5 | 67.21 |
八年级 | 83.7 | 96 | 88.5 | 183.68 |
(3)请根据上述统计图表中的信息,分析哪个年级对节约用水相关知识掌握的较好,说明理由.
【解答】解:(1)∵28%,
∴28%,
∴n=45.
七年级成绩在80≤x<90的有:84,89,89,85,84,83,83,共7人,
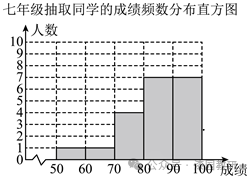
故答案为:45;
(2)∵92出现了5次,出现的次数最多,
∴七年级的众数是92.
∵20×45%=9,
∴八年级成绩的中位数在80≤x<90之间,
∵80≤x<90之间的数据从小到大排列为:81,85,88,89,
∴八年级的中位数为(88+89)÷2=88.5.
故答案为:92,88.5;
(3)∵七年级的平均成绩高,方差小,
∴七年级对节约用水相关知识掌握的较好.
22.(12分)如图,抛物线y=ax2+2ax+c经过A(﹣3,0),B(0,4)两点.
(1)求抛物线的函数表达式;
(2)点C为直线AB上方抛物线上一动点,过点C作CD⊥AB,垂足为点D,作CE∥y轴,交AB于点E,求CD+CE的最大值及此时点C的坐标.
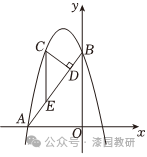
【解答】解:(1)将A(﹣3,0),B(0,4)两点代入y=ax2+2ax+c,
得,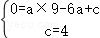
解得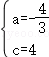
则抛物线的表达式为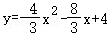 ;
;
(2)根据A(﹣3,0),B(0,4)得,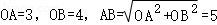
∵CE∥OB,
∴∠CED=∠ABO,
∵在Rt△AOB中,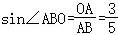
∴
∵CD⊥AB,
则 .
.
设直线AB的表达式为y=mx+n,
将A(﹣3,0),B(0,4)两点代入得: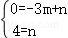
解得: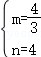
故直线AB的表达式为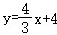
设点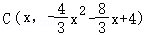 ,则点
,则点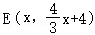
则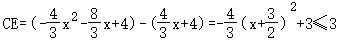
即CE的最大值为3,CD+CE的最大值为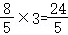
此时点C的坐标为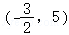 .
.
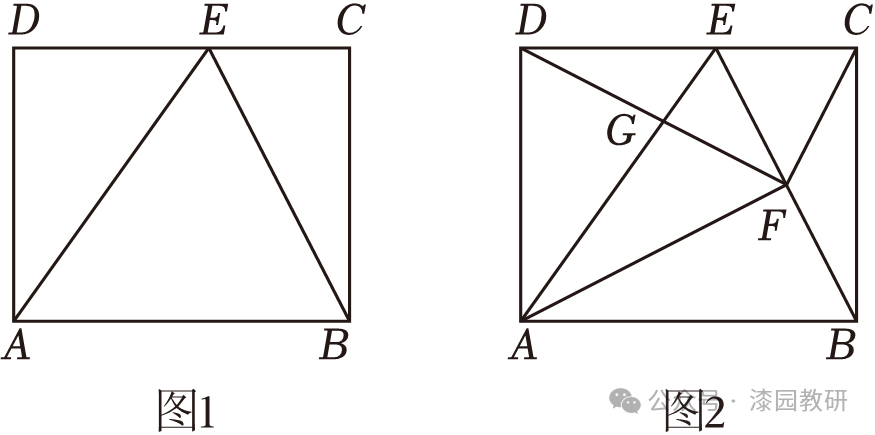
23.(14分)在矩形ABCD中,E是AB上一点,连接AE,BE,BE平分∠AEC.
(1)如图1,求证:AE=CD;
(2)如图2,取BE中点F,连接AF,DF,CF,AE与DF交于点G.
①求∠CFD的度数;
②若tan∠CBE=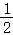 =6,求FG的长.
=6,求FG的长.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠ABE=∠CEB.
∵BE平分∠AEC,
∴∠AEB=∠CEB,
∴∠A E B=∠A B E,
∴AE=AB,
∴AE=CD;
(2)解:①∵在△ABE中,AE=AB,F是BE的中点,
∴AF⊥BE,
∴∠AFB=90°.
∵FC是Rt△BCE的中线,
∴EF=CF=BF,
∴∠CEF=∠ECF;
∵AB∥CD,
∴∠CEF=∠ABF,
∴∠ECF=∠ABF,
在△DCF和△ABF中,
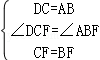
∴△DCF≌△ABF(SAS),
∴∠CFD=∠AFB=90°;
②∵∠CDF+∠DCF=∠CEB+∠CBE=90°,∠CEF=∠ECF,
∴∠CDF=∠CBE,
∴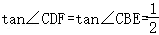 .
.
设CE=a,则CB=2a,
由勾股定理得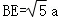 ,得
,得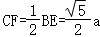
∵在Rt△CFD中,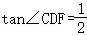
∴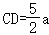
∴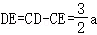 .
.
延长DF交AB的延长线于H,
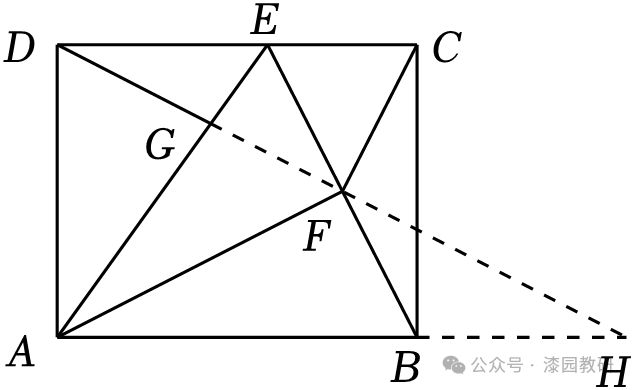
∵四边形ABCD是矩形,
∴CD∥AB,
∴∠CDF=∠BHF,
∵F为BE的中点,
∴FE=FB,
又∠DFE=∠HFB,
∴△DEF≌△HBF,
∴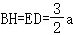 =FH,
=FH,
∵AB∥CD,
∴△DEG∽△HAG,
∴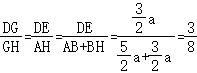
∵DG=6,
∴GH=16,
∴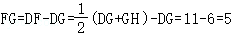 .
.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/6/3 22:33:16;用户:mczl58;邮箱:ldwh135@xyh.com;学号:24737059







