圆幂定理总结,帮你突破中考数学几何压轴瓶颈!

【圆幂定理总结，帮你突破中考数学几何压轴瓶颈！】

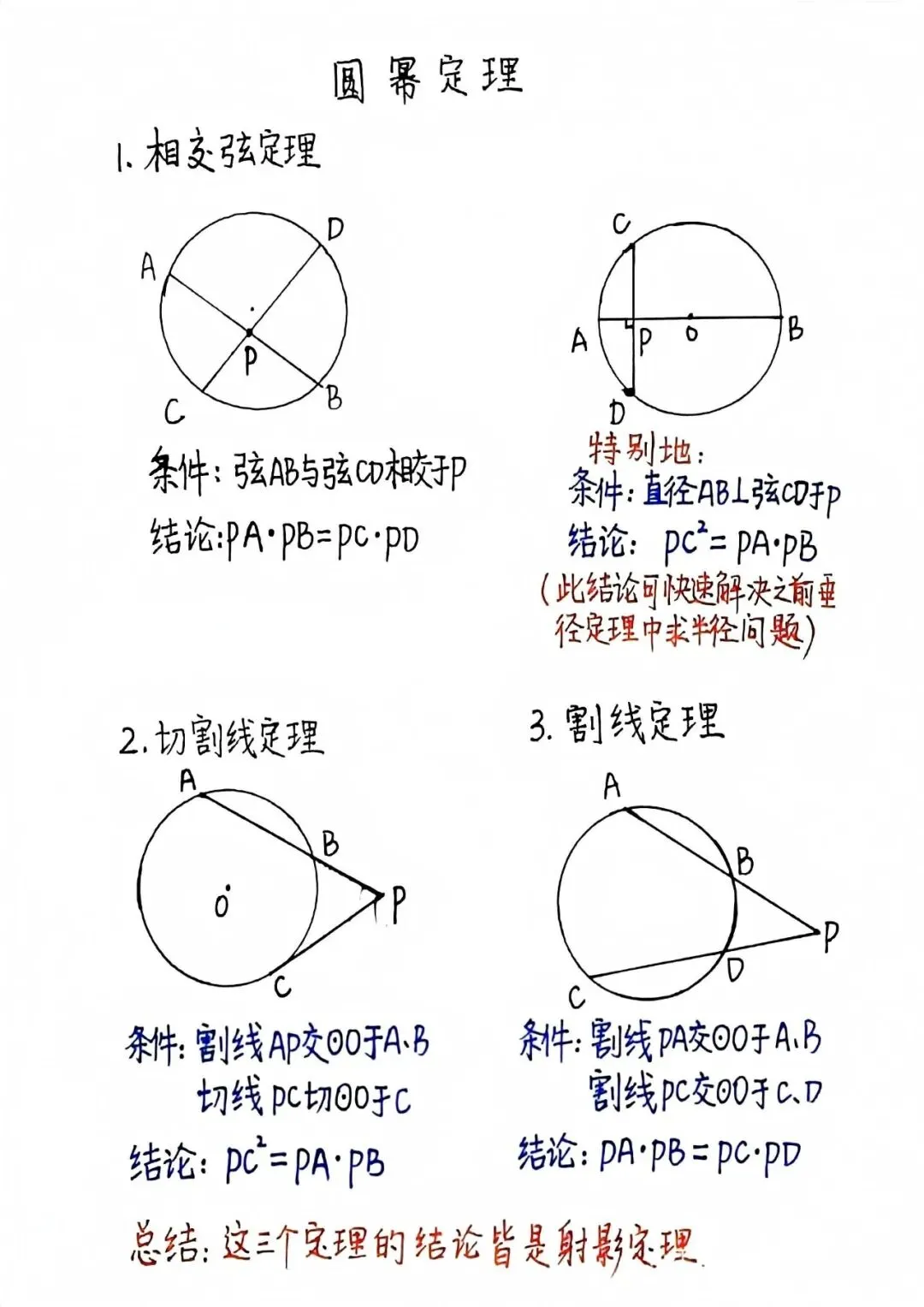
圆幂定理作为平面几何的核心定理体系，揭示了点与圆位置关系的深刻规律。该定理包含三个相互关联的组成部分，共同构建起完整的几何认知框架。

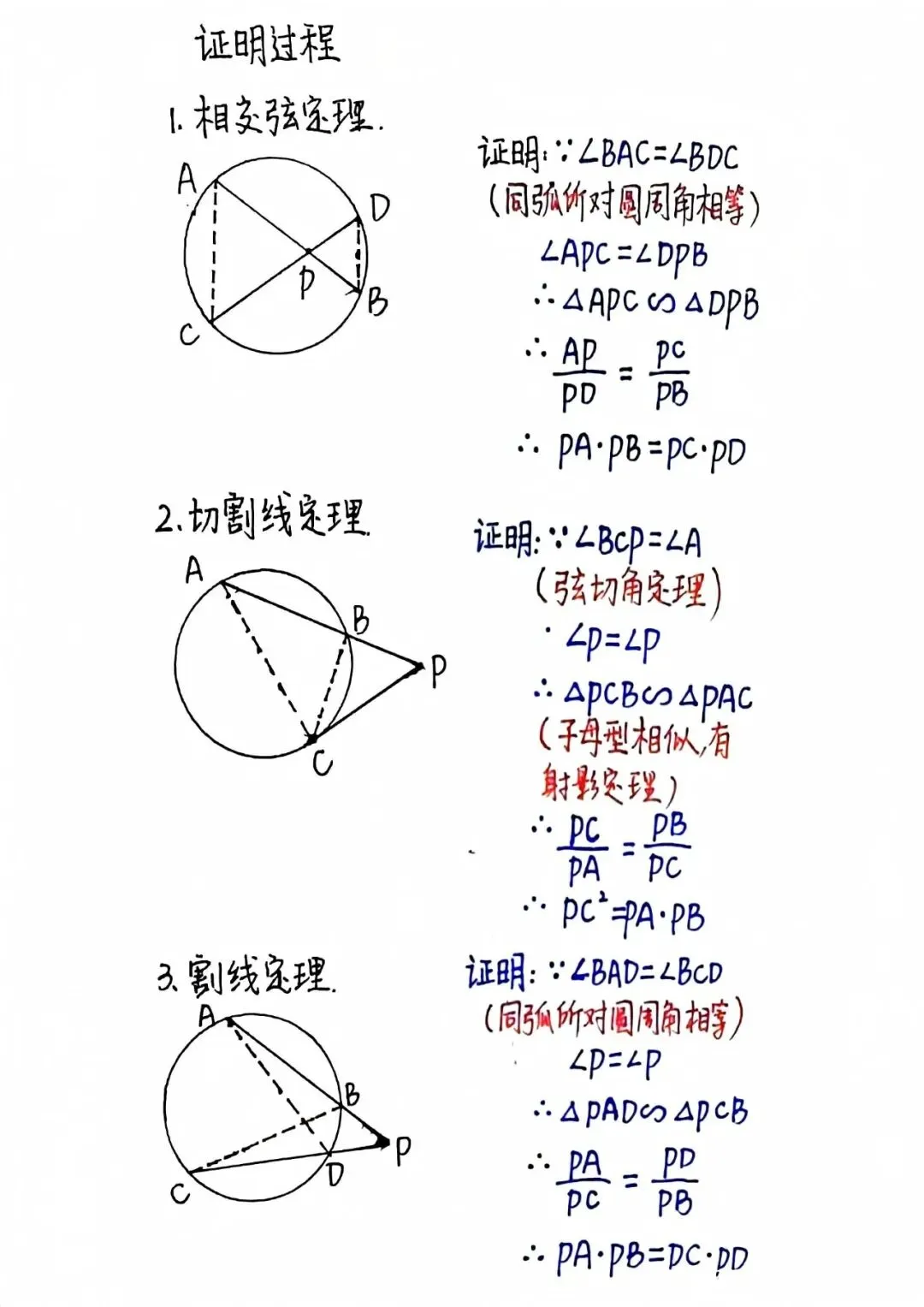
首先是相交弦定理：当圆内两条弦AB与CD相交于点P时，存在定量关系PA·PB=PC·PD。这个优美的等式犹如精密的几何天平，无论弦如何旋转，交点两侧线段长度的乘积始终保持动态平衡。其证明可通过相似三角形（△APC∽△DPB）完成，体现了圆内接四边形对角互补的特性。

其次是切割线定理的经典表述：从圆外一点P引切线PA（A为切点）和割线PBC（B、C为交点），则PA²=PB·PC。这一结论仿佛几何世界的能量守恒定律，将切线这个"瞬时接触"转化为可度量的比例关系。其证明既可利用弦切角定理，也可通过△PAB∽△PCA的相似关系建立。

最后是割线定理的普遍形式：对于圆外任意点P，若引出两条割线PAB和PCD（A、B、C、D均为交点），则PA·PB=PC·PD。这个结论如同几何交响乐中的复调旋律，与相交弦定理形成完美的对应关系。其证明方法多样，既可通过辅助线构造相似三角形，也可借助幂的几何意义进行推导。

这三个定理构成有机整体，统一于"点对圆的幂"这一核心概念——即定点P到圆O的幂定义为OP²-R²（R为圆半径）。当点在圆外时幂为正，圆内为负，圆上为零。这种统一视角不仅揭示了定理间的内在联系，更为解析几何中圆方程的研究埋下伏笔。