(47)2025年苏州市中考
工业园区一模数学第27题
数学实验:折叠正方形纸片。
通过纸片的折叠,可以发现许多有趣
的现象,这些现象可以用有关的数学
原理进行分析,解释,所以纸片的
折叠是一种有效的数学学习方式,
如图1, PQ是将正方形纸片ABCD
折叠后得到的一条折痕,其中点P, Q
分别在边AD,CD上.
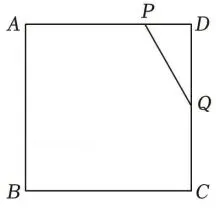
图1
(1)折叠正方形纸片ABCD,使得PA,
CQ依次落在直线PQ上。请你利用
无刻度直尺和圆规,在图1中分别作出
折痕PE, QF(不写作法,保留作图痕迹),
其中点E, F分别在边BC, AB上.设PE,
QF的交点为 O ,则∠POQ=______°,
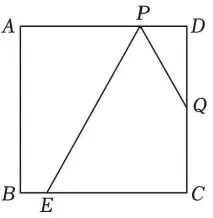
图2
(2)在⑴的条件下,折叠正方形纸片
ABCD,使得BC落在直线PQ上.请你
利用无刻度直尺和圆规,在图2中作出
折痕MN(不写作法,保留作图痕迹),
其中点M, N分别在边AB, CD上。
设MN, PE的交点为G,则点G落在正方
形纸片ABCD的哪一条对称轴上?请说明
理由:
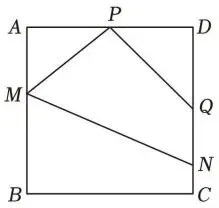
图3
(3)如图3,已知正方形纸片ABCD的
边长为16cm,在⑵的条件下,当点P
为边AD的中点时,则随着点Q位置的
改变,△PAM的周长是否会发生改变?
如果不变,求出△PAM的周长;如果
改变,求出△PAM的周长的最小值,
并求出此时折痕MN的长。
【解析】(1)如图4,
作∠APQ , ∠CQP的角平分线即可,
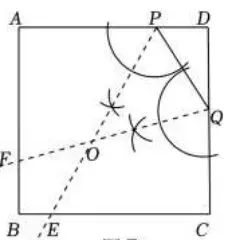
图4
∵∠APQ=∠D+∠DQP ,
∠CQP=∠D+∠DPQ,
∴∠APQ+∠CQP=∠D+∠DQP
+∠D+∠DPQ
=∠D+180°
=270°,
∵PE, OF分别是∠APQ, ∠CQP
的角平分线,
∴∠OPQ+∠OQP=1/2(∠APQ+∠CQP)
=135°,
∴∠POQ=180°-∠OPQ-∠OQP
=180°-135°
=45°,
故答案为:45,
(2)如图5,延长PQ , BC交于T ,
作∠BTP的角平分线即可,
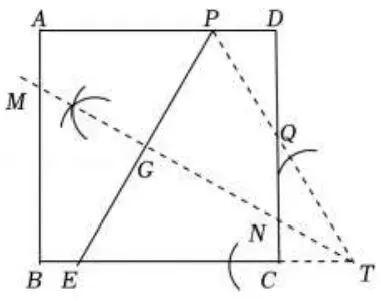
∵AD//BC ,
∴∠APE=∠PEC ,
∵PE平分∠APQ ,
∴∠APE=∠TPE ,
∴∠PEC=∠TPE ,
∵TG平分∠BTP .
∴∠PTG=∠ETG ,
又∵TG=TG ,
∴△PTG≌△ETG (AAS),
∴点G是PE的中点,
∴点G在边AB,CD的垂直平分线上,
(3)如图6,作∠MPQ的角平分线
交BC于E,连接ME ,
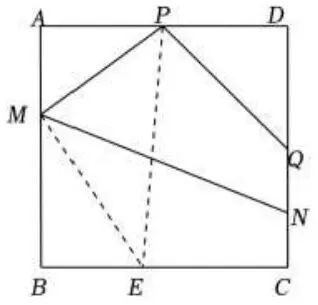
图6
∵MN是折痕,
∴MP=ME,
且MN垂直平分BP ,
∴C△PAM=AP+AM+MP
=AP+AM+ME ,
∵AP为定值
即 AP=1/2AD=8cm.
∴ 当A,M,E三点共线时,
AM+ME最小,
最小值即为AB的长,
故C△PAM的最小值为24cm,
此时E和B重合,将MN向上平移
使得M与A重合,如图7,
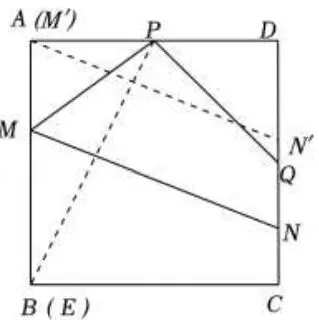
图7
∵∠PM'N'+∠BM'N'=90°,
∠M'BP+∠BM'N'=90°,
∴∠PM'N'=∠M'BP ,
∵M'B=M'D ,
∠BM'P=∠M'DN=90°,
∴△BM'P =△M'DN' (ASA),
∴ BP=M'N',
即 BP=MN ,
∵BP=√(AB²+AP²)
=√(16²+8²)
=8√5( cm ),
∴MN=8√5cm.
往期文章







