(42)2025年重庆市中考
长寿区一模数学第26题
在Rt△ABC中,∠BAC=90°,
AB=AC=5√2,点D是线段BC上一点,
连接AD .
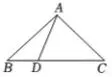
图1
(1)如图1,当CD=7时,
求线段AD的长,
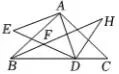
图2
(2)如图2,将线段AD绕点A顺时针
旋转90°得到线段AE,连接DE,点F
是DE的中点,连接BF并延长到点H,
连接DH ,若2∠BHD+∠HBC=90°,
①求证: FH=1/2DE+CD,
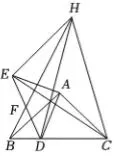
图3
②如图3,连接CE,CH,EH,点D
从点B移动到点C的过程中,当BF取得
最小值时,请直接写出△CEH的面积.
【解析】(1)如图4,过点A作AE⊥BC
于点E ,
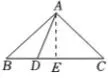
图4
∵△BAC=90°, AB=AC=5√2,
∴BC=√2AB=10,
AE=BE=CE
=1/2BC=5,
∵CD=7,
∴DE=2,
∴AD=√(AE²+DE²)
=√(5²+2²)
=√29,
(2)①证明:如图5,连接BE,AF ,
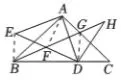
由旋转得
AD=AE , ∠DAE=90°,
∵∠BAC=90°,
AB=AC=5√2,
∴∠BAE=∠CAD ,
∴△BAE≌△CAD (SAS),
∴ BE=CD ,
∠ABE=∠ACB
=∠ABC
=45°,
∴∠EBC=90°,
∵点F是DE的中点,
∴ AF=EF=DF=BF ,
在FH上截取FG=EF,连接DG ,
∵∠BFE=∠DFG ,
∴△BFE≌△DFG (SAS),
∴∠FDG=∠FBE
=∠FEB
=∠FGD ,
DG=BE=CD ,
∵2∠BHD+∠HBC=90°,
∠EBH+∠HBC=90°,
∴∠EBH =2∠BHD,
∴∠FGD =2∠BHD,
∵∠FGD=∠BHD+∠GDH,
∴∠BHD=∠GDH ,
∴DG=GH ,
∴GH=CD ,
∵FH=FG+GH ,
∴FH=EF +CD ,
即 FH=1/2DE+CD ,
②解:如图6,连接BE ,
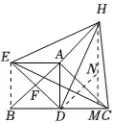
图6
由①得∠EBD =90°,
∴BF=1/2DE ,
∴DE=√2AD,
∴当AD最小时, BF的值最小,
此时 AD⊥BC ,
则 DE⊥AB ,
∴AD=BD=CD
=1/2BC=5,
BF=AF=DF
=EF=√2/2BD
=5√2/2,
∵2∠BHD+∠HBC=90°,
∠ABD=∠BAD=45°,
∴∠BHD=22.5°,
∴∠ADH=22.5°,
∴ AH=AD=5,
∠HDC=67.5°,
∴FH=5√2/2+5,
如图6,过点H作HM⊥BC于点M,
在HM上截取HN=HA ,连接DN ,
∴△AHD≌△NHD (SAS),
∴DN=AD= AH=HN=5,
∵∠HDN=∠DHN=22.5°,
∴∠DNM=45°,
∴DM=MN=√2/2DN==5√2/2 ,
HM=5√2/2+5,
∴S△CEH=S△DEH+S△CDH
-S△CDE
=1/2DE·FH +1/2CD·HM
-1/2CD·BE
=1/2x5√2x(5√2/2+5)
+1/2x5x(5√2/2+5)
-1/2x5x5
=(75√2+50)/4 .
往期文章







