学
习
数
学
丘班/自招/中考/高联/强基/高考
王子文老师
4个定义-3个公式-4个诱导公式
定义1:sinα,cosα,tanα,cotα.
例题1:已知α与斜边,求邻边与对边.
例题2:已知α与邻边,求斜边与对边.
例题3:已知α与对边,求斜边与邻边.
公式2:c^2+s^2=1,tanαcotα=1,t=s/c.
例题4:已知cosα=c,求sinα,tanα.
例题5:已知sinα=s,求cosα,tanα.
例题6:已知tanα=y/x,求cosα,sinα.
公式3-1:sin(90°-α)=cosα.
公式3-2:cos(90°-α)=sinα.
公式3-3:tan(90°-α)=cotα.
公式3-4:cot(90°-α)=tanα.
例题7:45°的各种三角值.
例题8:60°与30°的各种三角值.
例题9:75°与15°的各种三角值.
半角公式:tan(α/2)=s/(1+c)=(1-c)/s.
注:可以拓展为6-7-4,高中学习6-7-16.
解三角形理论(a,b,c,A,B,C)
SSS,ASS,SAS,SSA,AAA,SAA,ASA,AAS.
第一步:ASS与SSA等价.
第二步:SAA与AAS等价.
剩下6种情况:SSS,SAS,SSA,AAA,ASA,AAS.
第三步:AAA不能确定三角形.
第四步:SSA在某些情况下不能确定三角形.
进而只需研究:SSS,SAS,ASA,AAS.
以锐角三角形为例有如下四个模板.
注:非锐角三角形也有类似模板成立.
按AAS,ASA,SAS,SSS的顺序总结.
第一阶段
例题1:已知α,β,α+β为锐角,求sin(α+β).
推论1:sin(α+β)/sinα=cotαsinβ+cosβ.
模板0:已知AA(B,C),求sinA.
推论2:sinA/sinC=cotCsinB+cosB.
模板1:已知AAS(B,C,c),求b.
模板1:已知AAS(B,C,c),求a.
模板2:已知ASA(B,C,a),求b,c.
模板3:已知SAS(b,c,A),求cotB,cotC.
模板3:已知SAS(b,c,A),求a.
模板4:已知SSS(a,b,c),求cosA,cosB,cosC.
例题2:a/sinA=b/sinB=c/sinC的四种证明方法.
观点1:例题1等价于模板0.
观点2:例题2能推出模板1,模板2,模板3,模板4.
注:模板3,4就是余弦定理(bsinA,c-bcosA,a).
注:例题2就是正弦定理(不含2R).
第二阶段
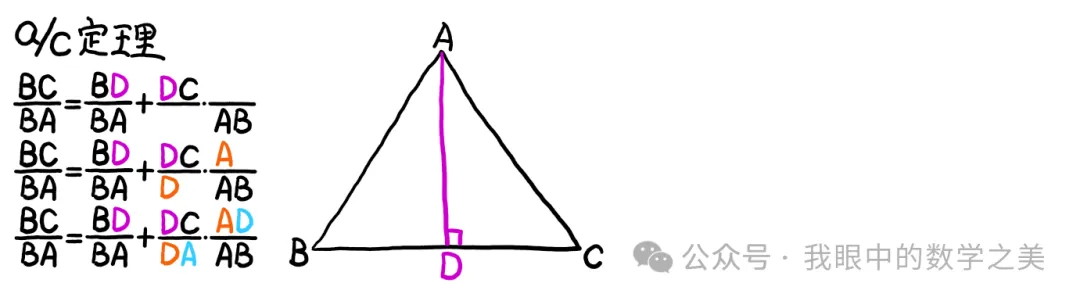
定理①:a/sinA=b/sinB=c/sinC的四种证明方法.
定理②:a/c=cotCsinB+cosB.
模板零:已知α,β,α+β为锐角,求sin(α+β).
模板①:已知AA(B,C),求sinA.
模板②:已知AAS(B,C,c),求b.
模板③:已知AAS(B,C,c),求a.
模板③:已知ASA(B,C,a),求b,c.
模板③:已知SAS(b,c,A),求cotB,cotC.
模板④:已知SAS(b,c,A),求a.
模板④:已知SSS(a,b,c),求cosA,cosB,cosC.
第三阶段
模板0-①之公式1-①
模板1-②之公式2-②
模板1-③之公式3-②
模板2-③之公式4-②
模板3-③之公式5-②
模板3-④之公式6-③
模板4-④之公式7-③
公式①:两角和公式
公式②:正弦定理
公式③:余弦定理
压轴题

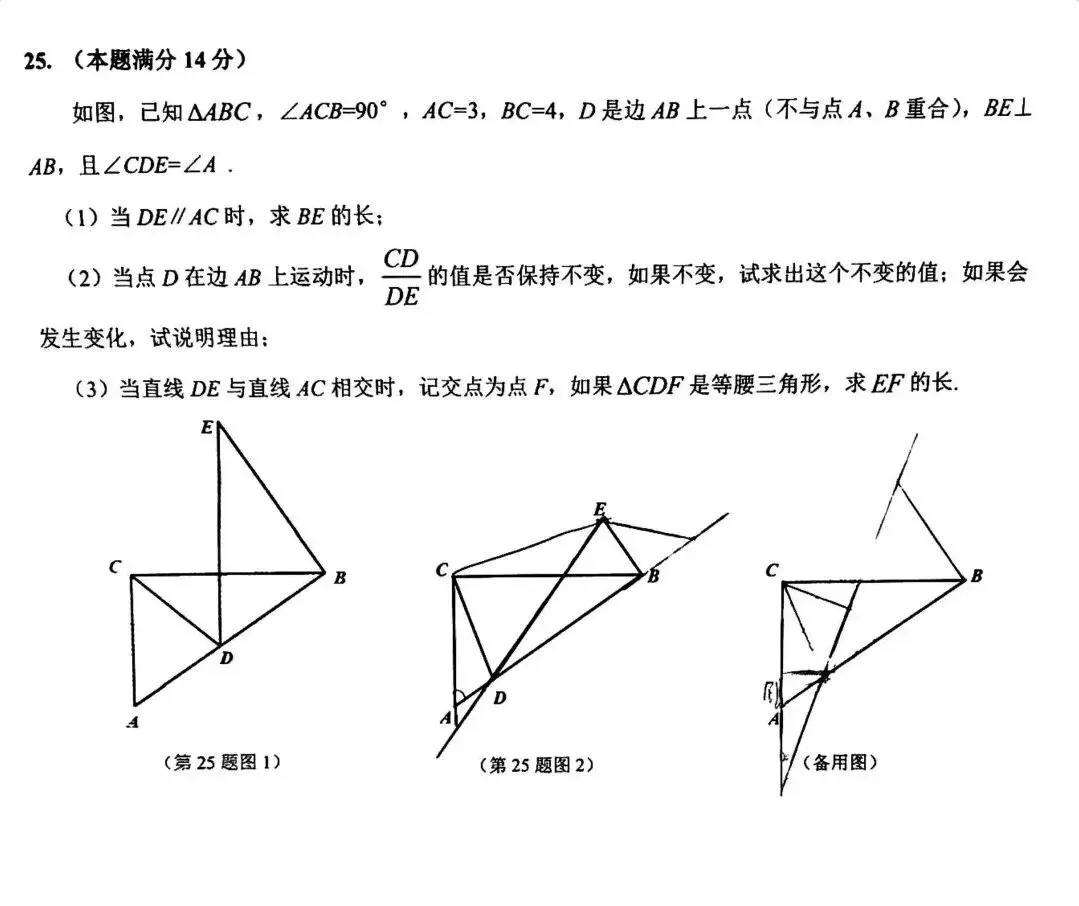
第25题
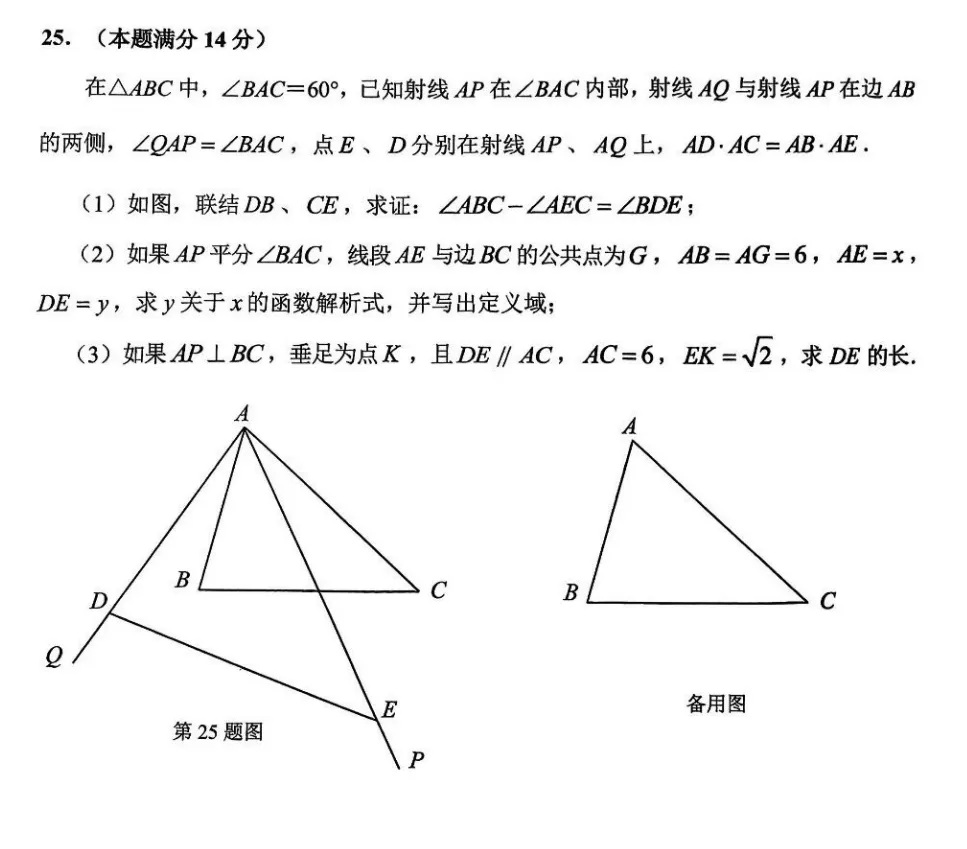
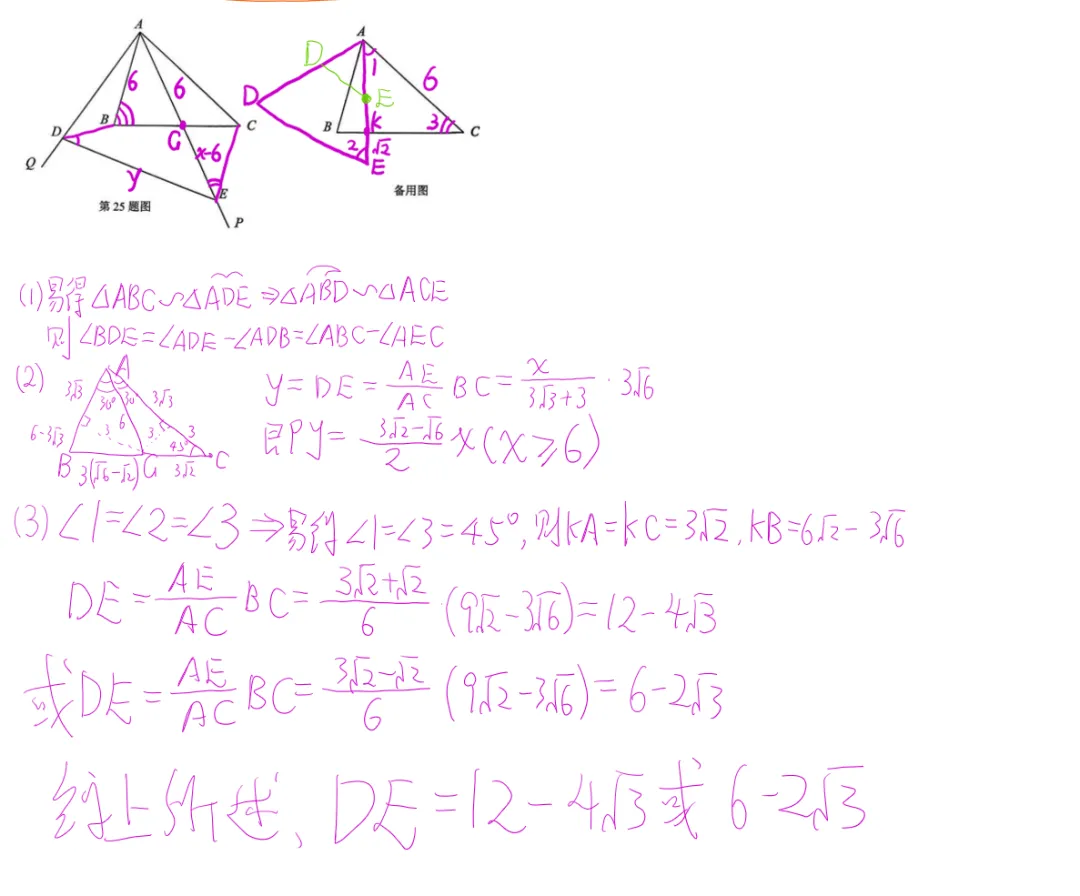
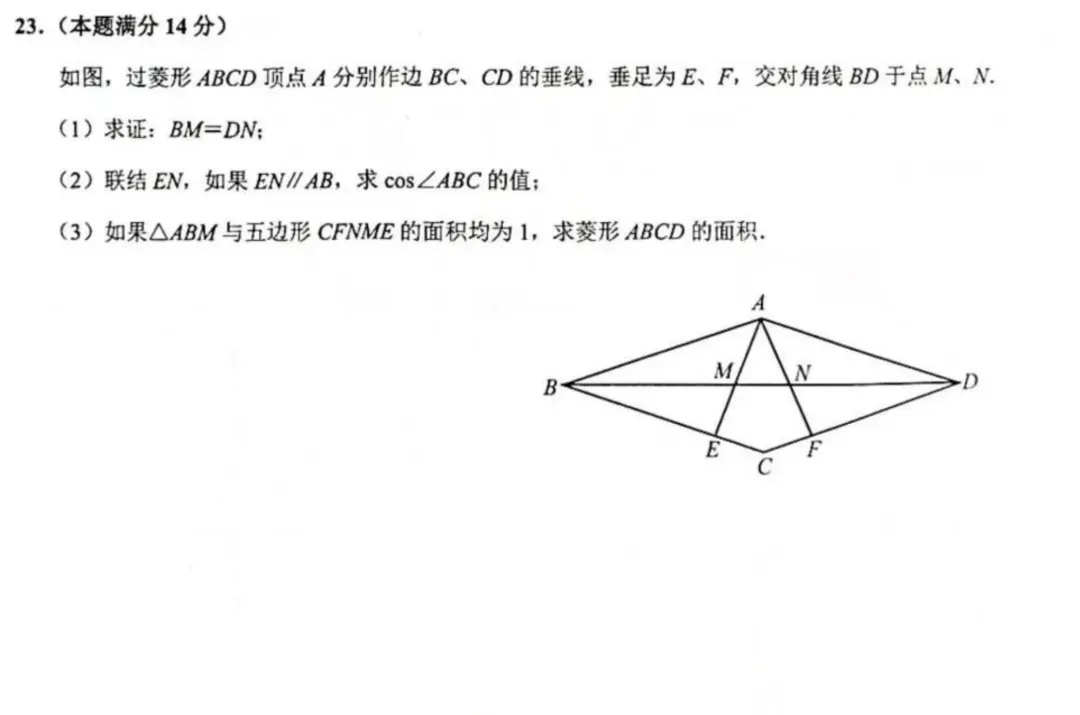


接受1-12年级的任何课程1对1,2,3+教学
01.自招初联之代数式,方程,不等式,函数;
02.自招初联之三角形,四边形,相似,圆;
03.自招初联之初等数论;
04.自招初联之组合数学;
05.中考数学之18题,24题,25题;
06.高中数学之必修1,2与选修1,2,3;
07.高考数学之11-12-15-16-20-21题;
08.强基高联之高中数学课本内容拓展;
09.高等数学之陈纪修编写的数学分析;
10.线性代数之谢启鸿编写的高等代数;
接受小奥升学1对1,2,3+补课需求
接受初中自招1对1,2,3+补课需求
接受数学中考1对1,2,3+补课需求
接受高联一试1对1,2,3+补课需求
接受高中强基1对1,2,3+补课需求
接受数学高考1对1,2,3+补课需求
如果您的孩子目前初三或者高一,本人可以赠送我参与编审的价值79元的书即“新高中数学同步全刷之必修一”(快递费需要你们自己付一下),微信二维码在下面,可以扫码加我,我来送书.

拓展链接






此二维码为初高中数学交流群,欢迎大家加入,本人会不定时分享一些数学知识,也会不定期做答疑;欢迎大家加我微信,我拉你们入群;






