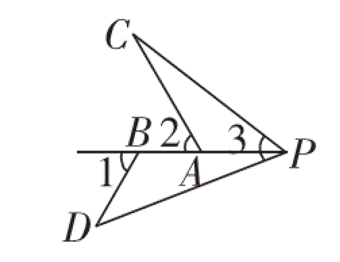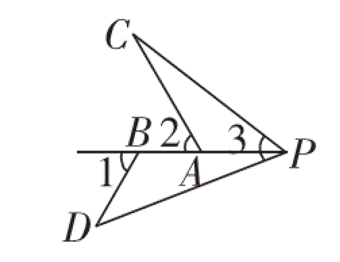典例【初步探究】
【变式探究1】
【变式探究2】
【变式探究2】
文章来源：
四季读书网
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请发送邮件至23467321@qq.com举报，一经查实，本站将立刻删除;如已特别标注为本站原创文章的，转载时请以链接形式注明文章出处，谢谢！
中考复习——一线三等角模型
4
0
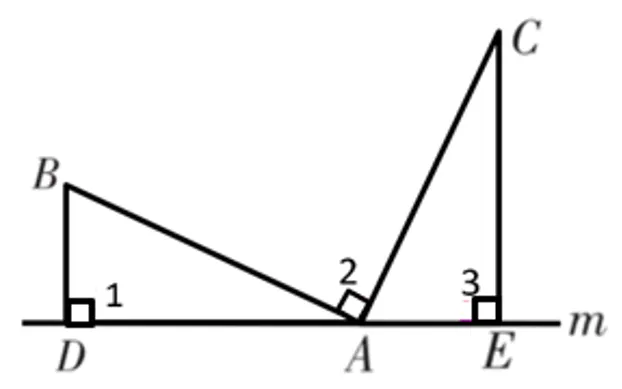
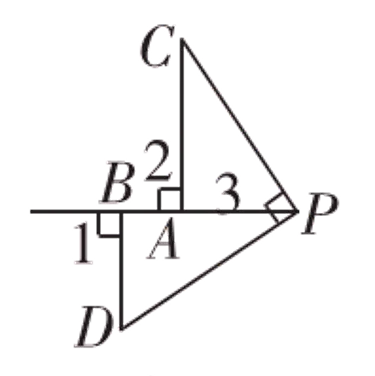
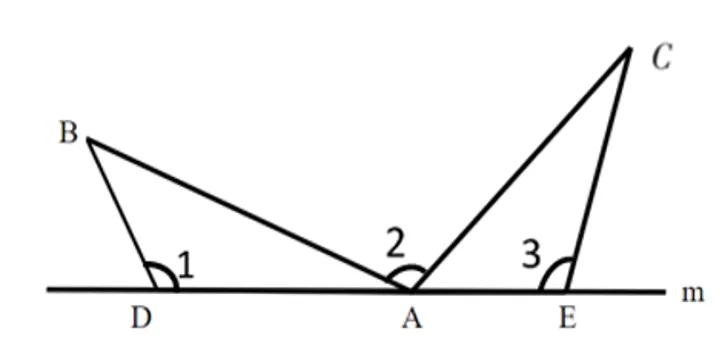
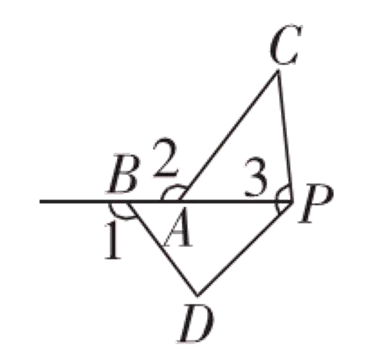
中考复习——一线三等角模型如图1，已知AB＝AC，∠2＝90°，直线m经过点A，过点B作BD⊥直线m于点D，过点C作CE⊥直线m于点E.写出线段DE，BD，CE之间的数量关系，并证明． 解：DE＝BD＋CE. 证明：∵∠2＝90°，∠1＝90°， ∴∠CAE+∠BAD＝90°，∠B＋∠BAD＝90° ∴∠B＝∠CAE. 又∵∠1＝∠3＝90°，AB＝CA， ∴△ADB≌△CEA(AAS)． ∴BD＝AE，AD＝CE. ∴DE＝AE＋AD＝BD＋CE. 如图2，已知AB＝AC，若∠1＝∠2＝∠3＝α°（0< α <180），则线段DE，BD，CE之间的数量关系仍然成立吗？如果成立，请证明；如果不成立，请说明理由． 解：线段DE，BD，CE之间的数量关系仍然成立． 证明：∵∠B＋∠BAD＝∠CAE＋∠BAD＝180°－α， ∴∠B＝∠CAE. 又∵∠1＝∠3＝α，AB＝CA， ∴△ADB≌△CEA(AAS)． ∴BD＝AE，AD＝CE. ∴DE＝AE＋AD＝BD＋CE. 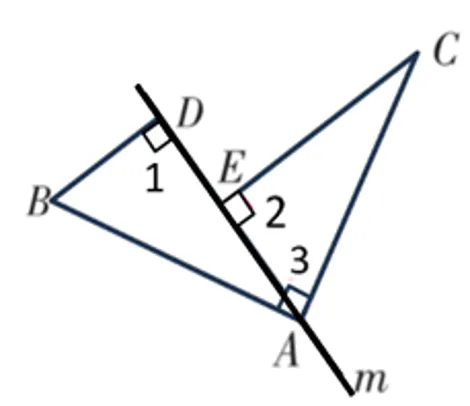已知AB＝AC，∠3＝90°，若直线m绕点A旋转至如图3所示的位置，过点B作BD⊥直线m于点D，过点C作CE⊥直线m于点E，则线段DE，BD，CE之间的数量关系仍然成立吗？如果成立，请证明；如果不成立，请写出正确的数量关系，并证明． 解：不成立，正确的数量关系为CE＝DE＋BD. 证明：∵∠3＝90°，∠1＝90°， ∴∠BAD＋∠CAE＝90°，∠BAD＋∠B＝90°. ∴∠CAE＝∠B. 又∵∠1＝∠2＝90°，AB＝CA， ∴△ADB≌△CEA(AAS)． ∴BD＝AE，AD＝CE. ∴CE＝AD＝DE＋AE＝DE＋BD. 已知DP＝CP，∠1＝∠2=∠3 = α°，则这两个三角形之间的关系是？
