中考数学考前强化练习之折叠在模型压轴选填题中应用
中考数学考前强化练习
折叠模型在压轴题中应用
矩形两次翻折 求线段长度 折叠模型
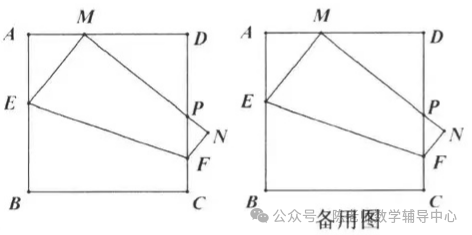
1.如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A'处,得到折痕BM,BM与EF相交于点N. 若直线BA'交直线CD于点0,BC=5,EN=1,则OD的长为()
A.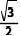 B.
B.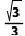 C.
C. 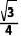 D.
D.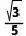
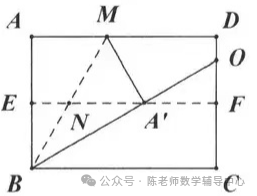
矩形折叠求线段长度
2.如图,直线EF是矩形ABCD的对称轴,点P在CD边上,将ΔBCP沿BP折叠,点C恰好落在线段AP与EF的交点Q处,BC=4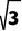 ,则线段AB的长是()
,则线段AB的长是()
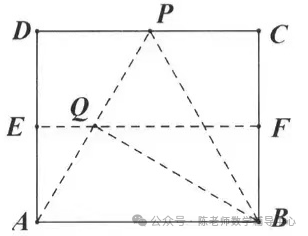
A. 8 B. 8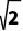 C. 8
C. 8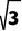 D. 10
D. 10
圆的翻折 对应角相等 对应弧相等
3.如图,AB是⊙0的直径,BC是⊙0的弦,先将BC弧沿BC翻折交AB于点D,再将BD弧沿AB翻折交BC于点E. 若BE弧=DE弧,设∠ABC=a,则a所在的范围是()
A. 21.90<a<22.3° C. 22.70<a<23.1°
B. 22.30<a<22.7° D. 23.10<a <23.5°
数学陈老师:
矩形折叠判断结论是否正确 选填压轴题
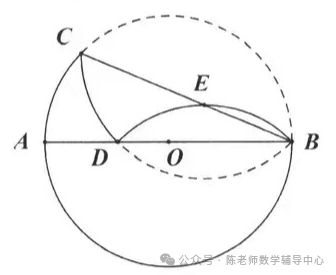
4.如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上。连接BG,交CD于点K,FG交CD于点H. 给出以下结论:①EF⊥BG;②GE=GF;③ΔGDK和ΔGKH的面积相等;④当点F与点C重合时,∠DEF=75°,其中正确的结论共有()
A.1个 B.2个 C.3个 D.4个
三角形纸片折叠 求距离
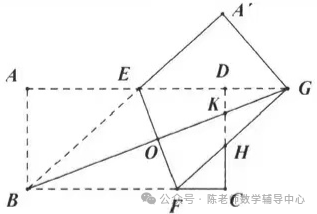
5.如图,三角形纸片ABC,点D是BC边上一点,连接AD,把ΔABD沿着AD翻折,得到ΔAED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,ΔADG的面积为2,则点F到BC的距离为( )
A. 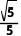 B.
B. 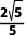 C.
C. 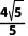 D.
D. 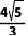
三角形纸折叠 求距离
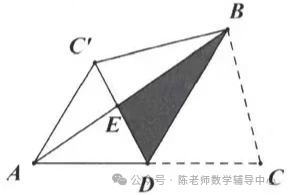
6.如图,在ΔABC中,D是AC边上的中点,连接BD,把ΔBDC沿BD翻折,得到ΔBDC',DC'与AB交于点E,连接AC',若AD=AC'=2,BD=3,则点D到BC'的距离为( )
A. 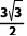 B.
B. 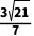 C.
C. 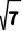 D.
D. 
矩形折叠 求角度的余弦值
7.如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将ΔCDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点0、F,且OP=OF,则cos∠ADF的值为()
A. 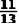 B.
B. 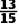 C.
C.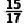 D.
D. 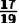 19
19
数学陈老师:
矩形折叠 多结论判断正误 选填压轴题题
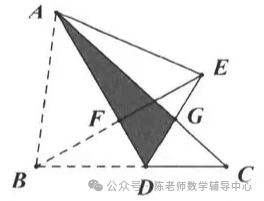
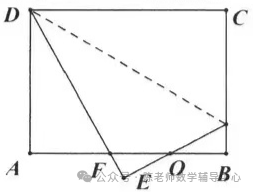
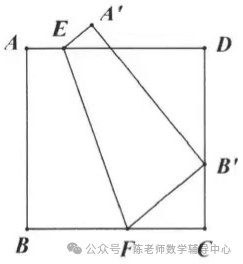
8.如图所示,在矩形纸片ABCD中,AB=3,BC=6,点E、F分别是矩形的边AD、BC上的动点,将该纸片沿直线EF折叠。使点B落在矩形边AD上,对应点记为点G,点A落在M处,连接EF、BG、BE,EF与BG交于点N. 则下列结论:①BN=AB;②当点G与点D重合时,EF=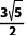 ;③ΔGNF的面积S的取值范围是9/4≤S≤7/2;④当CF=5/2时,SΔMEG=
;③ΔGNF的面积S的取值范围是9/4≤S≤7/2;④当CF=5/2时,SΔMEG=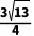 。其中成立的是()
。其中成立的是()
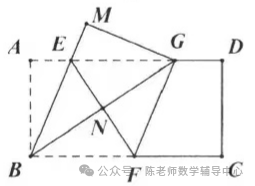
A. ①③ B.③④ C. ②③ D. ②④
矩形折叠 求线段长
9.如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点0.若AE=5,BF=3,则A0的长为()
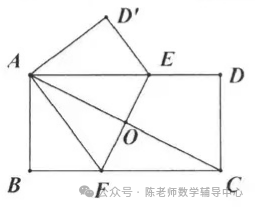
A. 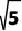 B.
B. 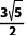 C. 2
C. 2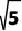 D. 4
D. 4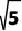
矩形折叠 求线段的比值
10.将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点0处,且点B,0,G在同一条直线上,同时点E,0,F在另一条直线上,则AD/AB的值为()
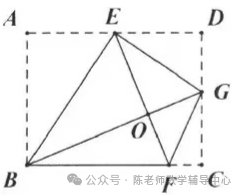
A. 6/5 B. 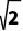 C. 3/2 D.
C. 3/2 D.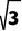
直角三角形折叠 求角度
11.如图,在RtΔABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将ΔACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于()
A. 120° B. 108° C. 72° D. 36°
数学陈老师:
正方形中的折叠 求线段的长常用方法
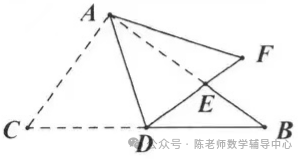
12.如图,已知正方形ABCD的边长为1,点E、F分别在边AD、BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点B'处,如果四边形ABFE与四边形EFCD的面积比为3:5,那么线段FC的长为 .
矩形折叠 求线段
13.如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连接EF.已知AB=3,BC=4,则EF的长为( )
A. 3 B. 5 C.5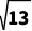 /6 D.
/6 D. 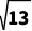
等边三角形折叠 求线段长 三角形相似
14.如图,DE平分等边ΔABC的面积,折叠ΔBDE得到ΔFDE,AC分别与DF,EF相交于G,H两点。若DG=m,EH=n,用含m,n的式子表示GH的长是 .
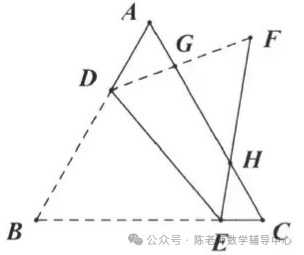
三角形折叠 求距离
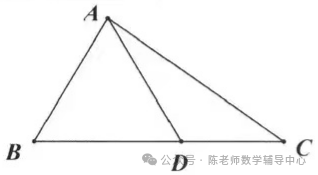
15.如图,在ΔABC中,AB=4,BC=7,∠B=60°,点D在边BC上,CD=3,连接AD. 如果将ΔACD沿直线AD翻折后,点C的对应点为点E,那么点E到直线BD的距离为 .
数学陈老师:
矩形折叠 等腰三角形存在性讨论
16.如图,在矩形ABCD中,AB=3,AD=4,E、F分别是边BC、CD上一点,EF⊥AE,将ΔECF沿EF翻折得ΔEC'F,连接AC',当BE= 时,ΔAEC'是以AE为腰的等腰三角形。
直接三角形折叠 求线段的长
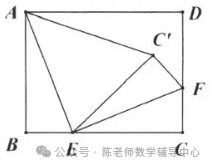
17.如图,在RtΔABC中,∠BAC=90°,AB=2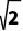 ,AC=6,点E在线段AC上,且AE=1,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,AF= .
,AC=6,点E在线段AC上,且AE=1,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,AF= .
矩形折叠 求线段长
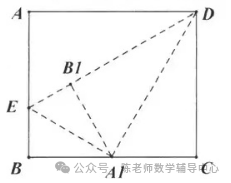
18.如图,在矩形ABCD中,AD=4,将∠A向内翻折,点A落在BC上,记为A1 ,折痕为DE.若将∠B沿EA1向内翻折,点B恰好落在DE上,记为B1 ,则AB= .
矩形折叠 求线段长 常用解决方法
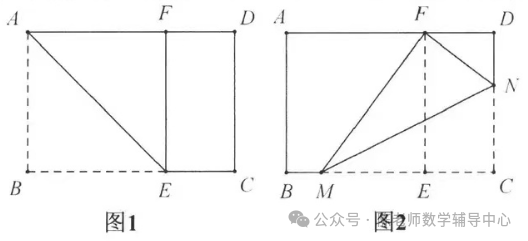
19.在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕MN,如图②.
根据以上的操作,若AB=8,AD=12,则线段BM的长是( )
A. 3 B. 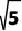 C. 2 D. 1
C. 2 D. 1
数学陈老师:
正方形折叠 求线段长
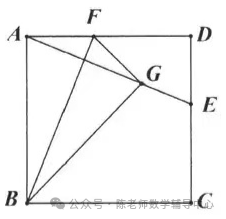
20.如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE、折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为 .
矩形折叠 求线段长
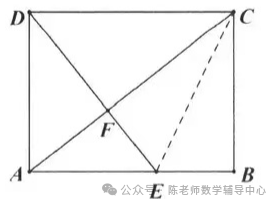
21.如图,是一张矩形纸片,点E在AB边上,把ΔBCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF= ,BE= .
矩形折叠 求角的正弦值
22.如图,矩形ABCD中,点G,E分别在边BC,DC上,连接AG,EG,AE,将ΔABG和ΔECG分别沿AG,EG折叠,使点B,C恰好落在AE上的同一点,记为点F. 若CE=3,CG=4,则sin∠DAE= .
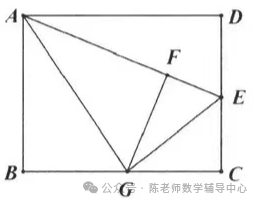
矩形折叠 求线段的长
23.如图,矩形ABCD中,AB=3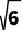 ,BC=12,E为AD中点,F为AB上一点,将ΔAEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是 .
,BC=12,E为AD中点,F为AB上一点,将ΔAEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是 .
数学陈老师:
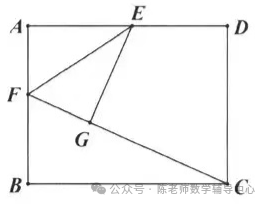
矩形纸片三步折叠操作 求线段的长
24.如图,已知矩形纸片ABCD,其中AB=3,BC=4,现将纸片进行如下操作:
第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;
第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;
第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.
则DH的长为()
A.3/2 B.8/5 C.5/3 D.9/5
矩形折叠 求矩形的面积
25.如图,矩形ABCD中,E为边AB上一点,将ΔADE沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点N,连接BN.若BF·AD=15,tan∠BNF=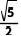 ,则矩形ABCD的面积为 .
,则矩形ABCD的面积为 .
矩形折叠 三角形相似 求正切值
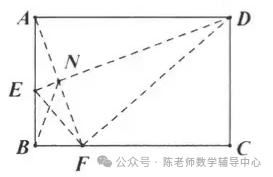
26.在矩形ABCD中,E为DC边上一点,把ΔADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:ΔABF≌ΔFCE;
(2)若AB=2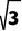 ,AD=4,求EC的长;
,AD=4,求EC的长;
(3)若AE-DE=2EC,记∠BAF=α,∠FAE=β,求tan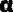 +tanβ的值.
+tanβ的值.
数学陈老师:
矩形折叠 三角形相似 求线段的比值
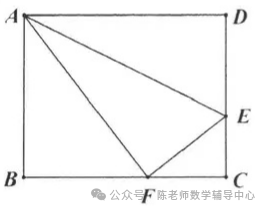
27.矩形ABCD中,AB=8,AD=12.将矩形折叠,使点A落在点P处,折痕为DE.
(1)如图①,若点P恰好在边BC上,连接AP,求AP/DE的值;
(2)如图②,若E是AB的中点,EP的延长线交BC于点F,求BF的长.
三角形折叠 求角度 求线段的长
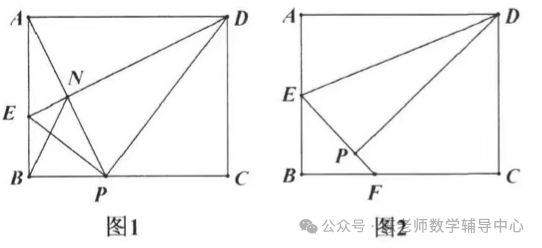
28.如图,在ΔABC中,AB=4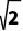 ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连接EF,沿EF将ΔAEF折叠得到ΔPEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连接AP,当PFLAC时,求AP的长.
数学陈老师:
矩形折叠 周长和面积的变化问题
29.如图,在边长为1的正方形ABCD中,动点E、F分别在边AB、CD上,将正方形ABCD沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A、D重合),点C落在点N处,MN与CD交于点P,设BE=x.
(1)当AM=1/3时,求x的值;
(2)随着点M在边AD上位置的变化,ΔPDM的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;
(3)设四边形BEFC的面积为S,求S与x之间函数表达式,并求出S的最小值.
直角三角形折叠 存在性问题探究
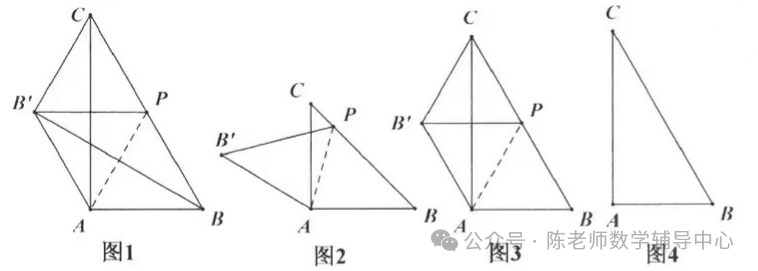
30.如图,在RtΔABC中,点P为斜边BC上一动点,将ΔABP沿直线AP折叠,使得点B的对应点为B',连接AB',CB',BB',PB'.
(1)如图①,若PB'⊥AC,证明:PB'=AB'.
(2)如图②,若AB=AC,BP=3PC,求cos∠B'AC的值.
(3)如图③,若∠ACB=30°,是否存在点P,使得AB=CB'.若存在,求此时PC/BC的值;若不存在,请说明理由。
点赞+关注
学习更优秀
打赏可获电子版





