2024中考数学 | 几何模型复习:动点最值之【费马点模型】提分必会

要知道今年你们将迎来人生中的第一次选拔性考试——中考，所以，这一年的时间都是很宝贵了。不想落后他人，预习复习工作都得做到位。今天，王老师和大家分享的是2024中考数学 | 几何模型复习：动点最值之【费马点模型】提分必会！

费马点模型：

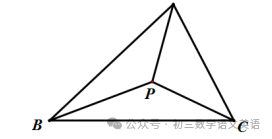
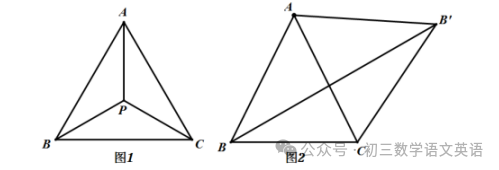
如图，在△ABC内部找到一点P，使得PA＋PB＋PC的值最小.

当点P满足∠APB＝∠BPC＝∠CPA＝120º，则PA＋PB＋PC的值最小，P点称为三角形的费马点.

特别地，△ABC中，最大的角要小于120º，若最大的角大于或等于120º，此时费马点就是最大角的顶点A

（这种情况一般不考，通常三角形的最大顶角都小于120°）

费马点的性质：

1．费马点到三角形三个顶点距离之和最小。

2．费马点连接三顶点所成的三夹角皆为120°。

费马点最小值解法：

以△ABC任意一边为边向外作等边三角形，这条边所对两顶点的距离即为最小值

证明过程：

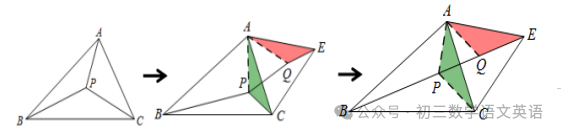
将△APC边以A为顶点逆时针旋转60°，得到AQE，连接PQ，则△APQ为等边三角形，PA=PQ。

即PA+PB+PC=PQ+PB+PC，当B、P、Q、E四点共线时取得最小值BE

【专项训练】

【例一】已知：△ABC是锐角三角形，G是三角形内一点。∠AGC=∠AGB=∠BGC=120°.求证：GA+GB+GC的值最小.

证明：将△BGC逆时针旋转60°，连GP,DB.则 △CGB≌△CPD；      

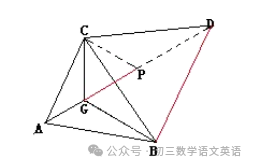
∴ ∠CPD=∠CGB=120°,CG=CP,

GB=PD, BC=DC,∠GCB=∠PCD.

∵ ∠GCP=60°,

∴ ∠BCD=60°,

∴ △GCP和△BCD都是等边三角形。

∵ ∠AGC=120°, ∠CGP=60°.

∴ A、G、P三点一线。

∵ ∠CPD=120°, ∠CPG=60°.

∴ G、P、D三点一线。

∴ AG、GP、PD三条线段同在一条直线上。

∵ GA+GC+GB=GA+GP+PD=AD.

∴ G点是等腰三角形内到三个顶点的距离之和最小的那一点

【例二】已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为√2+√6，求正方形的边长．

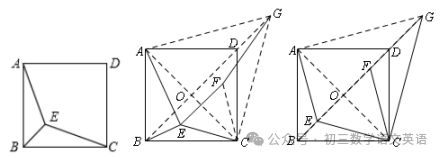
解：如图，连接AC，把△AEC绕点C顺时针旋转60°，得到△GFC，连接EF、BG、AG，

可知△EFC、△AGC都是等边三角形，则EF=CE．又FG=AE，

∴AE+BE+CE = BE+EF+FG．

∵ 点B、点G为定点（G为点A绕C点顺时针旋转60°所得）．

∴ 线段BG即为点E到A、B、C三点的距离之和的最小值，此时E、F两点都在BG上．

设正方形的边长为a，那么BO=CO=√2/2a，GC=√2a, GO=√6/2a．

∴ BG=BO+GO =√2/2a+√6/2a．

∵ 点E到A、B、C三点的距离之和的最小值为√2+√6．

∴ √2/2a+√6/2a=√2+√6，解得a=2．

【例三】如图，已知矩形ABCD，AB=4，BC=6，点M为矩形内一点，点E为BC边上任意一点，则MA+MD+ME的最小值为______．

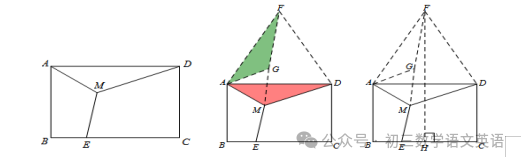
【解析】依然构造60°旋转，将三条折线段转化为一条直线段．

分别以AD、AM为边构造等边△ADF、等边△AMG，连接FG，

易证△AMD≌△AGF，∴MD=GF

∴ME+MA+MD=ME+EG+GF

过F作FH⊥BC交BC于H点，线段FH的长即为所求的最小值4+3√3

【例四】如图，P是锐角△ABC所在平面上一点，如果∠APB＝∠BPC＝∠CPA＝120°，则点P就叫做△ABC费马点。

（1）当△ABC是边长为4的等边三角形时，费马点P到BC边的距离为  2/3√3  ；

解：延长AP，交BC于D，如图所示：

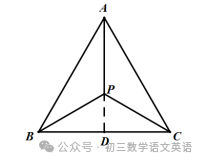
∵AB＝AC＝BC，∠APB＝∠BPC＝∠CPA＝120°，

∴P为三角形的内心，

∴AD⊥BC，BD＝CD＝2，∠PBD＝30°

∴BP=2/cos30°=4√3/3，

∴AP=BP=4√3/3，

∵AD=√AB²-BD²=2√3，

∴PD=AD-AP=2√3-4√3/3=2/3√3;

（2）若点P是△ABC的费马点，∠ABC＝60°，PA＝2，PC＝3，则PB的值为 √6 ；

解：∵∠PAB＋∠PBA＝180°－∠APB＝60°，∠PBC＋∠PBA＝∠ABC＝60°，

∴∠PAB＝∠PBC，

又∵∠APB＝∠BPC＝120°，

∴△ABP∽△BCP，

∴PA/PB=PB/PC，

∴PB²=PA×PC

即PB=√2×3=√6;

（3）如图2，在锐角△BC外侧作等边△ACB'，连接BB'.求证：BB'过△ABC的费马点P.

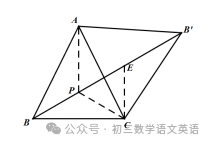
证明：在BB'上取点P，使∠BPC＝120°，连接AP，再在PB'上截取PE＝PC，连接CE，如图所示：

∵∠BPC＝120°，

∴∠EPC＝60°，

∴△PCE为正三角形，

∴PC＝CE，∠PCE＝60°，∠CEB'＝120°

∵△ACB'为正三角形，∴AC＝B'C，∠ACB'＝60°，

∴∠PCA＋∠ACE＝∠ACE＋∠ECB'＝60°，

∠PCA＝∠ECB'，∴△ACP≌△B'CE，

∴∠APC＝∠B'EC＝120°，PA＝EB'，

∠APB＝∠APC＝∠BPC＝120°，

∴P为△ABC的费马点，

∴BB'过△ABC的费马点P.