中考备考: 初中数学【相似三角形的判定】6大重难点题型专练
四季读书网
38
“草,在结它的种子,风,在摇它的叶子,我们俩站着不说话。”在顾城的诗里,陪伴就是这样简单而美好。 求学的阶梯会有很多步,幼儿园、小学、初中、高中(中专)、大学(大专)……这每一步的提升,都将需要刻苦的钻研和不断的求索才能实现。同学们,新的学期,新的征程,应有新的收获。新的学期,新的起点,应有新的面貌。荣誉的桂冠往往要拼搏编就,目标的实现往往需要坚持不懈的追求,征途的路往往靠脚踏实地的奋斗。新学期,希望你们能开启求学之门,学会知识;开启兴趣之门,学会方法;开启宽容之门,学会快乐;开启智慧之门,学会适应;开启真诚之门,学会相处!而在我们每一个人的生命里,会遇到各种各样的陪伴,比如说这会儿,你我之间是一段短暂的陪伴;比如说我们的学生时代,和我们的同学,那是几年的陪伴;还有一种陪伴,是生命里血脉注定一生的陪伴,那是我们和父母,和孩子之间的陪伴。北岳如行陪伴你一起开启学习之旅……
在同学们学习过程中,如果小学、初中、高中的知识有不清楚的地方,这里有名家讲课音视频、拓展内容、图文讲解、重难点分析、同步练习等等。在高考、中考期间,侧重高考、中考提前复习,分析历年高中考政策、各名校测试卷、各类易错题型,纵向练习。同时,为了课程的连续性,链接有小学基础知识。以后同年级各学科不同版本的教材也涉及,拓宽知识面,希望同学们能从中受益。这是初心,也是使命。
由于本人能力有限,可能出现各种各样的失误与不足,请大家提出宝贵的意见和建议,同时,我们可以共同交流探讨进步,不断提高作品的含金量。如果有好的内容和文章,大家可以推荐给我,让更多的学生从中受益。十年树木,百年树人。“为中华复兴而读书”!
同学们学习之余,可以点点关注,也可以看看文中的广告,也可以发表自己的观点、自己的作品、自己的经验,也可以把它分享给你的同学及好友,以促进栏目越办越好。
题型1 相似三角形的判定(判定定理1)
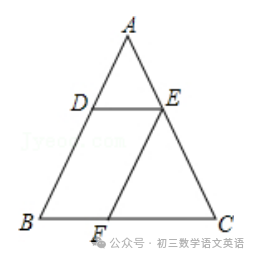
【例题】如图,在△ABC中,四边形DBFE是平行四边形.求证:△ADE∽△EFC.
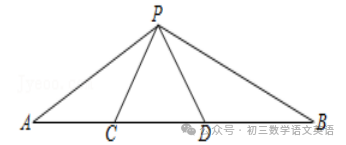
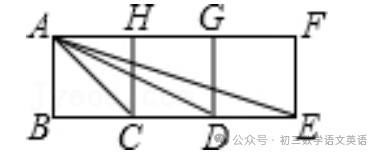
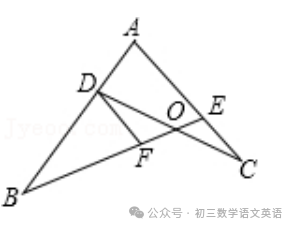
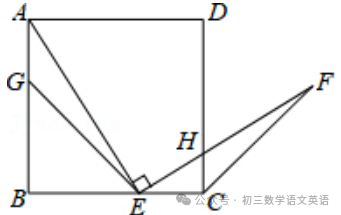
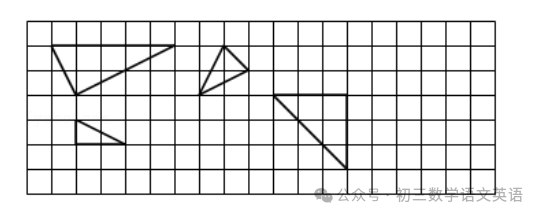
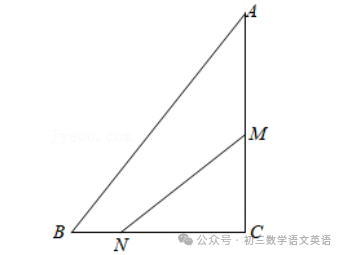
【例题】如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△PBD.根据等腰三角形的性质得出∠PCD=∠PDC,根据三角形的外角性质得出∠A+∠APC=∠PCD,∠B+∠BPD=∠PDC,求出∠B=∠APC,再根据相似三角形的判定推出即可.∵∠A+∠APC=∠PCD,∠B+∠BPD=∠PDC,【例题】如图,在矩形ABEF中,四边形ABCH、四边形CDGH和四边形DEFG都是正方形,图中的△ACD与△ECA相似吗?请说明理由.设小正方形的边长为1,分别求得两个三角形各边的长,再根据各边是否对应成比例来判定两三角形是否相似.则AC=√2,CD=1,AD=√5,EC=2,EA=√10,【例题】如图,点D,E分别在线段AB和AC上,BE与CD相交于点O,AD•AB=AE•AC,DF∥AC,求证:△DOF∽△DOB.根据相似三角形的判定得出△ABE与△ACD相似,利用相似三角形的性质得出∠B=∠C,再利用平行线的性质和相似三角形的判定解答即可.【例题】如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=DH;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH.其中,正确的结论有( )由∠BEG=45°知∠BEA>45°,结合∠AEF=90°得∠HEC<45°,据此知HC<EC,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△GAE≌△CEF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.解:∵四边形ABCD是正方形,∴AB=BC=CD,∵∠AEF=90°,∴∠HEC<45°,则HC<EC,∴CD﹣CH>BC﹣CE,即DH>BE,故①错误;∵BG=BE,∠B=90°,∴∠BGE=∠BEG=45°,∴∠AGE=135°,∴∠GAE+∠AEG=45°,∵∠BEG=45°,∴∠AEG+∠FEC=45°,∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,【例题】如图所示的4个三角形中,相似三角形有( )先分别求出三角形的三条边,根据相似三角形的判定方法判断即可.解:第一个三角形的三边的三边之比为:1:2:√5,第二个三角形的三边的三边之比为:√2:√5:√5,【例题】如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.(1)经过几秒后,△MCN的面积等于△ABC面积的2/5?(1)设经过x秒,△MCN的面积等于△ABC面积的2/5,根据三角形的面积和已知列出方程,求出方程的解即可;(2)根据相似三角形的判定得出两种情况,再求出t即可.解:(1)设经过x秒,△MCN的面积等于△ABC面积的2/5.1/2x2x(8-x)=1/2x8x10x2/5.答:经过4秒后,△MCN的面积等于△ABC面积的2/5;①MC/BC=NC/AC,即2t/8=8-t/10,②MC/AC=NC/BC,即2t/10=8-t/8.答:经过16/7或2t/10=8-t/840/13秒,△MCN与△ABC相似.免责声明:本文所有图文、音视频均来自网络,仅供学习交流使用,由北岳如行整理编辑,转载请注明,版权归原作者所有,除非无法确认,我们都会标明作者及出处,如有侵权烦请告知,我们会立即删除并表示歉意。谢谢!
点击阅读原文,开启同学们的理想冲刺之旅
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!