压轴题解题技巧题型分类解说
一、 对称翻折平移旋转
1．（南宁）如图12，把抛物线
（1）分别写出抛物线与
（2）设是抛物线上与
（3）在抛物线上是否存在点，使得，如果存在，求出点的坐标，如果不存在，请说明理由.
2．（福建宁德）如图，已知抛物线C1：的顶点为P，与x轴相交于A、B两点（点A在点B的左边），点B的横坐标是1．
（1）求P点坐标及a的值；（4分）
（2）如图（1），抛物线C2与抛物线C1关于x轴对称，将抛物线C2向右平移，平移后的抛物线记为C3，C3的顶点为M，当点P、M关于点B成中心对称时，求C3的解析式；（4分）
（3）如图（2），点Q是x轴正半轴上一点，将抛物线C1绕点Q旋转180°后得到抛物线C4．抛物线C4的顶点为N，与x轴相交于E、F两点（点E在点F的左边），当以点P、N、F为顶点的三角形是直角三角形时，求点Q的坐标．（5分）
二、 动态：动点、动线
3．(辽宁锦州)如图，抛物线与x轴交于A(x1，0)、B(x2，0)两点，且x1＞x2，与y轴交于点C(0，4)，其中x1、x2是方程x2－2x－8＝0的两个根．
(1)求这条抛物线的解析式；
(2)点P是线段AB上的动点，过点P作
PE∥AC，交BC于点E，连接CP，当△CPE
的面积最大时，求点P的坐标；
(3)探究：若点Q是抛物线对称轴上的点，
是否存在这样的点Q，使△QBC成为等腰三
角形？若存在，请直接写出所有符合条件的
点Q的坐标；若不存在，请说明理由．
4．（山东青岛）已知：如图①，在Rt△ACB中，∠C＝90°，AC＝4cm，BC＝3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），解答下列问题：
（1）当t为何值时，PQ∥BC？
（2）设△AQP的面积为y（），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；
（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．
5．（吉林省）如图所示，菱形ABCD的边长为6厘米，∠B＝60°．从初始时刻开始，点P、Q同时从A点出发，点P以1厘米/秒的速度沿A→C→B的方向运动，点Q以2厘米/秒的速度沿A→B→C→D的方向运动，当点Q运动到D点时，P、Q两点同时停止运动．设P、Q运动的时间为x秒时，△APQ与△ABC重叠部分的面积为y平方厘米（这里规定：点和线段是面积为0的三角形），解答下列问题：
（1）点P、Q从出发到相遇所用时间是 秒；
（2）点P、Q从开始运动到停止的过程中，当△APQ是等边三角形时x的值是 秒；
（3）求y与x之间的函数关系式．
6．(浙江嘉兴)如图，已知A、B是线段MN上的两点，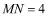
，
，
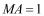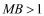．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成△ABC，设
．
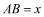（1）求x的取值范围；
（2）若△ABC为直角三角形，求x的值；
（3）探究：△ABC的最大面积？
三、 圆
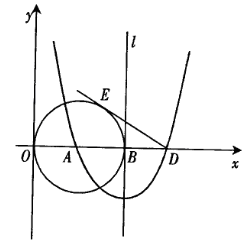
7．（青海） 如图10，已知点A（3，0），以A为圆心作⊙A与Y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l.
（1）以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；
（2）抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求此切线长；
（3）点F是切线DE上的一个动点，当△BFD与EAD△相似时，求出BF的长 ．
8．(天水)如图1，在平面直角坐标系xOy，二次函数y＝ax2＋bx＋c(a＞0)的图象顶点为D，与y轴交于点C，与x轴交于点A、B，点A在原点的左侧，点B的坐标为(3，0)，OB＝OC，tan∠ACO＝．
(1)求这个二次函数的解析式；
(2)若平行于x轴的直线与该抛物线交于点M、N，且以MN为直径的圆与x轴相切，求该圆的半径长度；
(3)如图2，若点G(2，y)是该抛物线上一点，点P是直线AG下方的抛物线上的一动点，当点P运动到什么位置时，△AGP的面积最大？求此时点P的坐标和△AGP的最大面积．
9．（湖南张家界）在平面直角坐标系中，已知A(－4，0)，B(1，0)，且以AB为直径的圆交y轴的正半轴于点C，过点C作圆的切线交x轴于点D．
（1）求点C的坐标和过A，B，C三点的抛物线的解析式；
（2）求点D的坐标；
（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由．
10．（潍坊市）如图，在平面直角坐标系中，半径为1的圆的圆心在坐标原点，且与两坐标轴分别交于四点．抛物线与轴交于点，与直线交于点，且分别与圆相切于点和点．
（1）求抛物线的解析式；
（2）抛物线的对称轴交轴于点，连结，并延长交圆于，求的长．
（3）过点作圆的切线交的延长线于点，判断点是否在抛物线上，说明理由．
四、比例比值取值范围
11．（怀化）图9是二次函数的图象，其顶点坐标为M(1,-4).
（1）求出图象与轴的交点A,B的坐标；
（2）在二次函数的图象上是否存在点P，使,若存在，求出P点的坐标；若不存在，请说明理由；
（3）将二次函数的图象在轴下方的部分沿轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线与此图象有两个公共点时，的取值范围.
12． (湖南长沙)如图，在平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上， cm， OC=8cm，现有两动点P、Q分别从O、C同时出发，P在线段OA上沿OA方向以每秒cm的速度匀速运动，Q在线段CO上沿CO方向以每秒1 cm的速度匀速运动．设运动时间为t秒．
（1）用t的式子表示△OPQ的面积S；
（2）求证：四边形OPBQ的面积是一个定值，并求出这个定值；
（3）当△OPQ与△PAB和△QPB相似时，抛物线经过B、P两点，过线段BP上一动点M作轴的平行线交抛物线于N，当线段MN的长取最大值时，求直线MN把四边形OPBQ分成两部分的面积之比．
13．（成都）在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，点的坐标为，若将经过两点的直线沿轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线．
（1）求直线及抛物线的函数表达式；
（2）如果P是线段上一点，设、的面积分别为、，且，求点P的坐标；
（3）设的半径为l，圆心在抛物线上运动，则在运动过程中是否存在与坐标轴相切的情况？若存在，求出圆心的坐标；若不存在，请说明理由．并探究：若设⊙Q的半径为，圆心在抛物线上运动，则当取何值时，⊙Q与两坐轴同时相切？
五、探究型
14．（内江）如图，抛物线与轴交于两点，与轴交于点.
（1）请求出抛物线顶点的坐标（用含的代数式表示），两点的坐标；
（2）经探究可知，与的面积比不变，试求出这个比值；
（3）是否存在使为直角三角形的抛物线？若存在，请求出；如果不存在，请说明
理由.
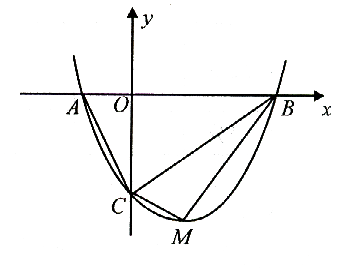
15．（重庆潼南）如图, 已知抛物线与y轴相交于C，与x轴相交于A、B，点A的坐标为（2，0），点C的坐标为（0，-1）.
（1）求抛物线的解析式；
（2）点E是线段AC上一动点，过点E作DE⊥x轴于点D，连结DC，当△DCE的面积最大时，求点D的坐标；
（3）在直线BC上是否存在一点P，使△ACP为等腰三角形，若存在，求点P的坐标，若不存在，说明理由.
16．（福建龙岩）如图，抛物线经过的三个顶点，已知轴，点在轴上，点在轴上，且．
（1）求抛物线的对称轴；
（2）写出三点的坐标并求抛物线的解析式；
（3）探究：若点是抛物线对称轴上且在轴下方的动点，是否存在是等腰三角形．若存在，求出所有符合条件的点坐标；不存在，请说明理由．
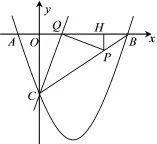
17．（广西钦州）如图，已知抛物线y＝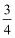
x2＋bx＋c与坐标轴交于A、B、C三点， A点的坐标为（－1，0），过点C的直线y＝
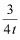x－3与x轴交于点Q，点P是线段BC上的一个动点，过P作PH⊥OB于点H．若PB＝5t，且0＜t＜1．
（1）填空：点C的坐标是_▲_，b＝_▲_，c＝_▲_；
（2）求线段QH的长（用含t的式子表示）；
（3）依点P的变化，是否存在t的值，使以P、H、Q为顶点的三角形与△COQ相似？若存在，求出所有t的值；若不存在，说明理由．
18．（重庆市）已知：如图，在平面直角坐标系xOy中，矩形OABC的边OA在轴的正半轴上，OC在轴的正半轴上，OA＝2，OC＝3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．
（1）求过点E、D、C的抛物线的解析式；
（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与轴的正半轴交于点F，另一边与线段OC交于点G．如果DF与（1）中的抛物线交于另一点M，点M的横坐标为，那么EF＝2GO是否成立？若成立，请给予证明；若不成立，请说明理由；
（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．
19．（湖南长沙）如图，抛物线y＝ax 2＋bx＋c(a≠0)与x轴交于A(－3，0)、B两点，与y轴相交于点C(0，)．当x＝－4和x＝2时，二次函数y＝ax 2＋bx＋c(a≠0)的函数值y相等，连结AC、BC．
（1）求实数a，b，c的值；
（2）若点M、N同时从B点出发，均以每秒1个单位长度的速度分别沿BA、BC边运动，其中一个点到达终点时，另一点也随之停止运动．当运动时间为t秒时，连结MN，将△BMN沿MN翻折，B点恰好落在AC边上的P处，求t的值及点P的坐标；
（3）在（2）的条件下，抛物线的对称轴上是否存在点Q，使得以B，N，Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由．
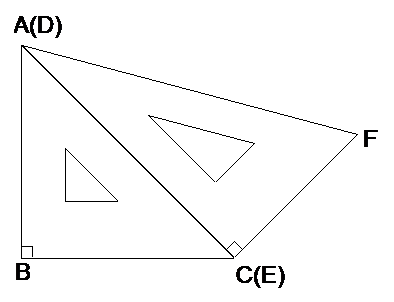
20．（江苏徐州）如图1，一副直角三角板满足AB＝BC，AC＝DE，∠ABC＝∠DEF＝90°，∠EDF＝30°
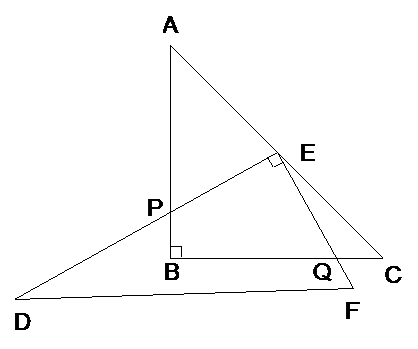
【操作】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB交于点P，边EF与边BC于点Q
【探究一】在旋转过程中，
（1） 如图2，当时，EP与EQ满足怎样的数量关系？并给出证明.
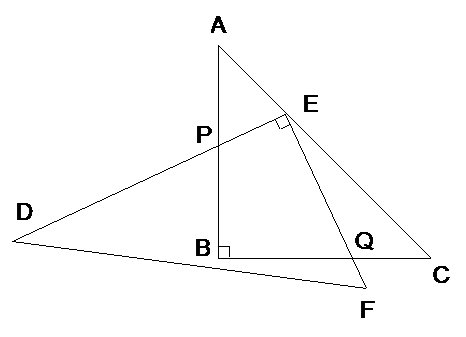
（2） 如图3，当时EP与EQ满足怎样的数量关系？，并说明理由.
（3） 根据你对（1）、（2）的探究结果，试写出当时，EP与EQ满足的数量关系式
为 ,其中的取值范围是 (直接写出结论，不必证明)
【探究二】若，AC＝30cm，连续PQ，设△EPQ的面积为S(cm2)，在旋转过程中：
（1） S是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由.
（2） 随着S取不同的值，对应△EPQ的个数有哪些变化？不出相应S值的取值范围.
六、最值类
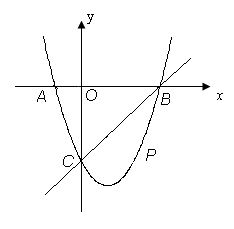
22．(恩施) 如图11，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点.
（1）求这个二次函数的表达式．
（2）连结PO、PC，并把△POC沿CO翻折，得到四边形POPC，那么是否存在点P，使四边形POPC为菱形？若存在，请求出此时点P的坐标；若不存在
请说明理由．
（3）当点P运动到什么位置时，四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
▍ 声明：本文整理自网络，如有侵权，请联系删除。
本公号刊载此文，是出于传递更多信息之目的。若有来源标注错误或侵犯了您的合法权益，请随时与我们联系协商，联系（QQ）：1146980684，我们将及时更正、删除。
