中考数学干货,全等三角形的10个模型,青岛大学生家教老师

1、基本模型

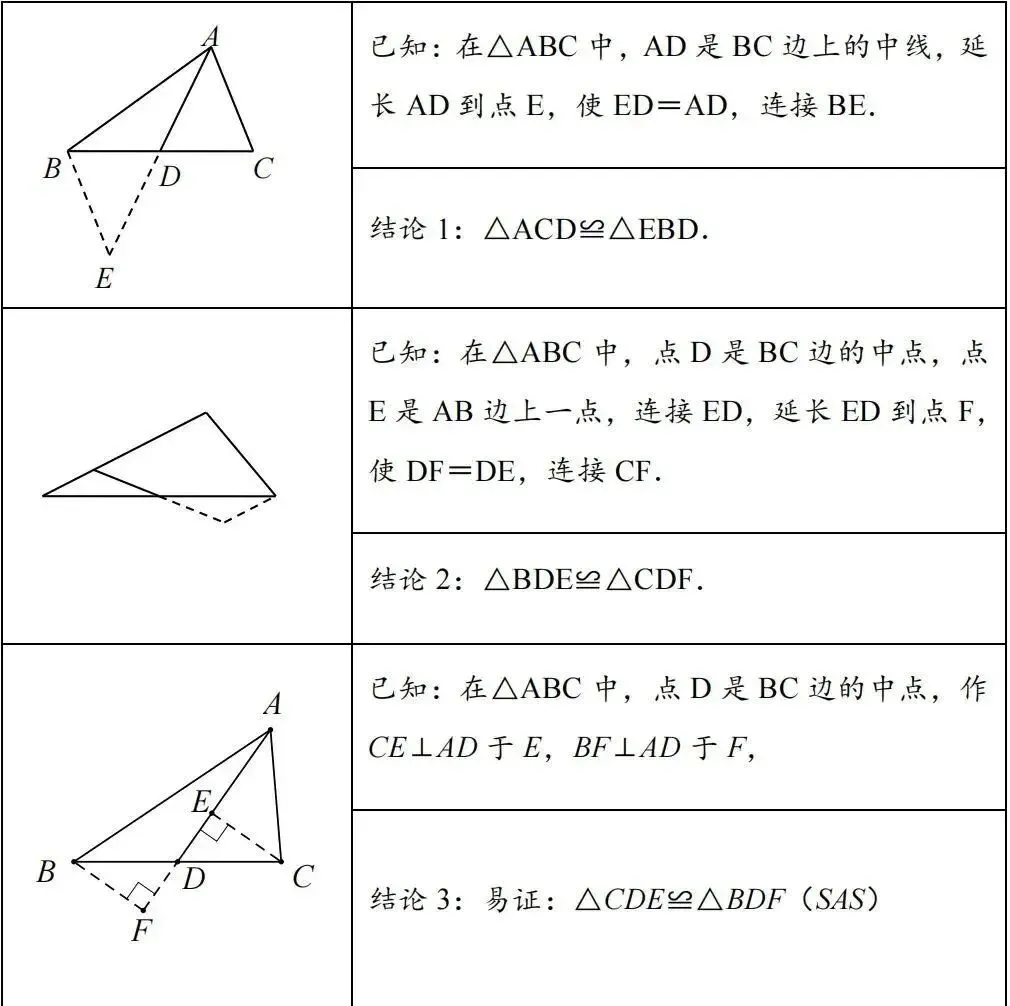
2、结论推导

3、解题技巧

遇到中点或中线，则考虑使用“倍长中线模型”，即延长中线，使所延长部分与中线相等，然后连接相应的顶点，构造出全等三角形．

4、历史文章

一题多解 | 中线倍长；

来解题吧 | 逆用倍长中线；

来解题吧 | 逆用倍长中线+翻折求最值；

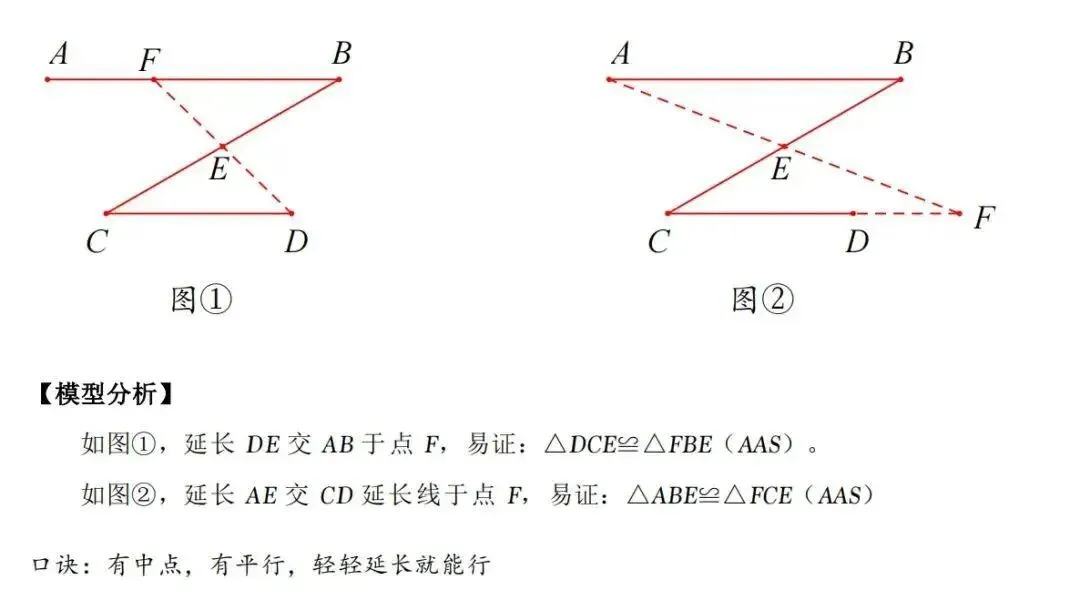
二、一线三等线模型‍‍

1、基本模型

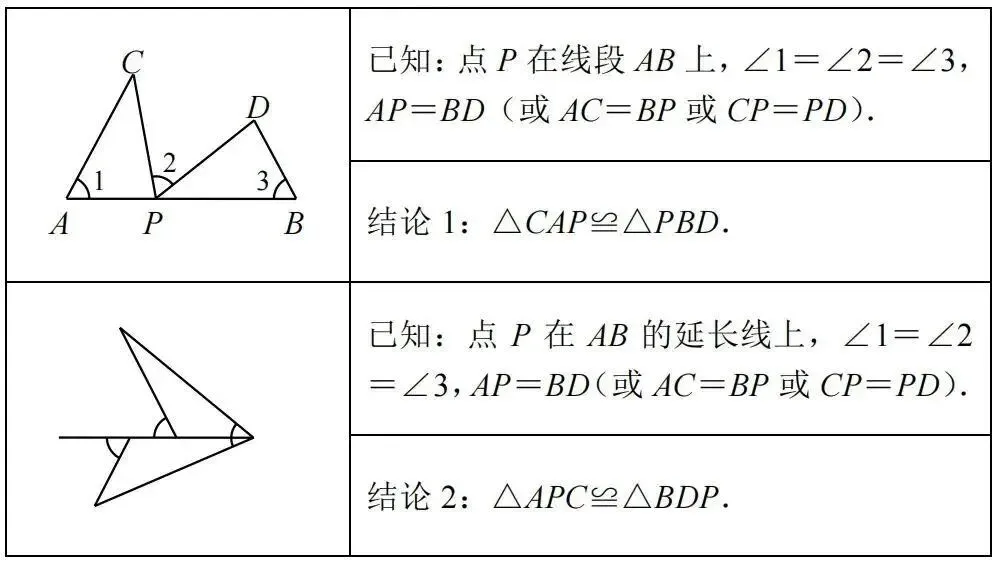
2、结论推导

结论1：△CAP≌△PBD．

证明：∵∠1＋∠C＋∠APC＝180°，∠2＋∠BPD＋∠APC＝180°，∠1＝∠2，∴∠C＝∠BPD．

∵∠1＝∠3，AP＝BD（或AC＝BP或CP＝PD），∴△CAP≌△PBD．

结论2：△APC≌△BDP．

证明：∵∠1＝∠C＋∠APC，∠2＝∠BPD＋∠D，∠3＝∠BPD＋∠APC，∠1＝∠2＝∠3，

∴∠C＝∠BPD，∠APC＝∠D．∵AP＝BD（或AC＝BP或CP＝PD），∴△APC≌△BDP．

三、半角模型

1、基本模型

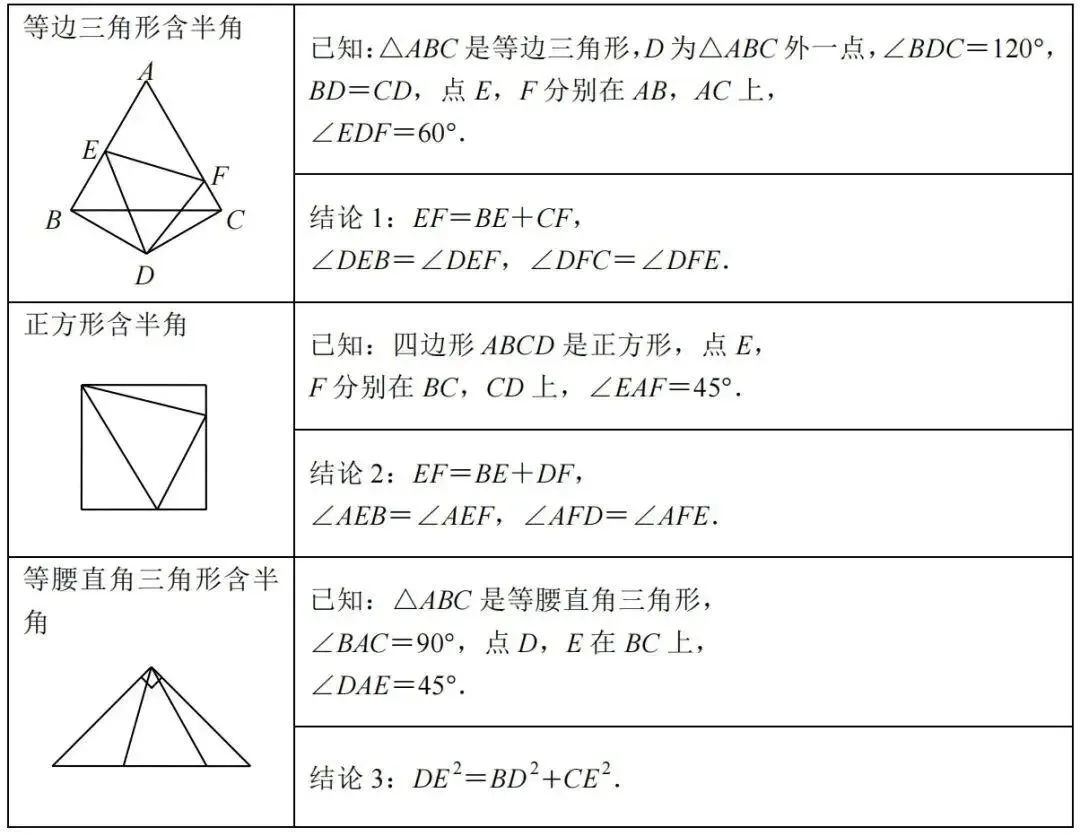
2、结论推导‍

四、手拉手模型

1、基本模型

2、结论推导

五、对角互补模型

1、基本模型

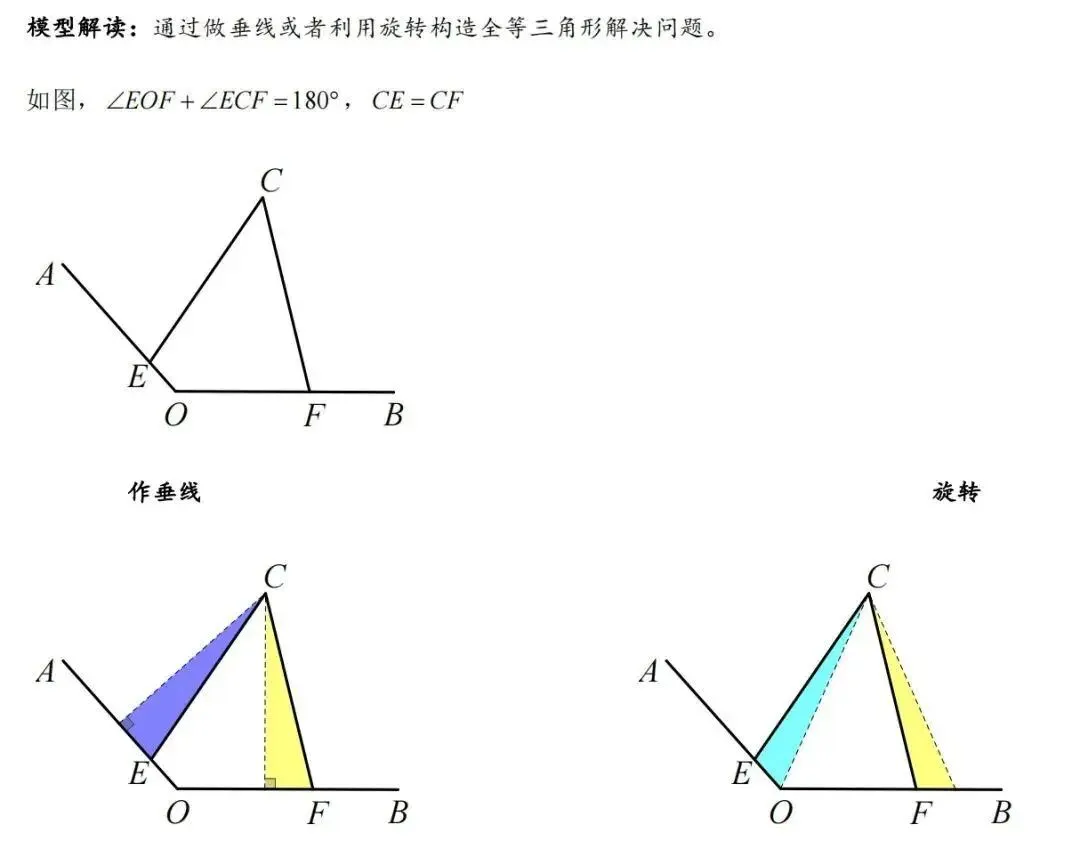
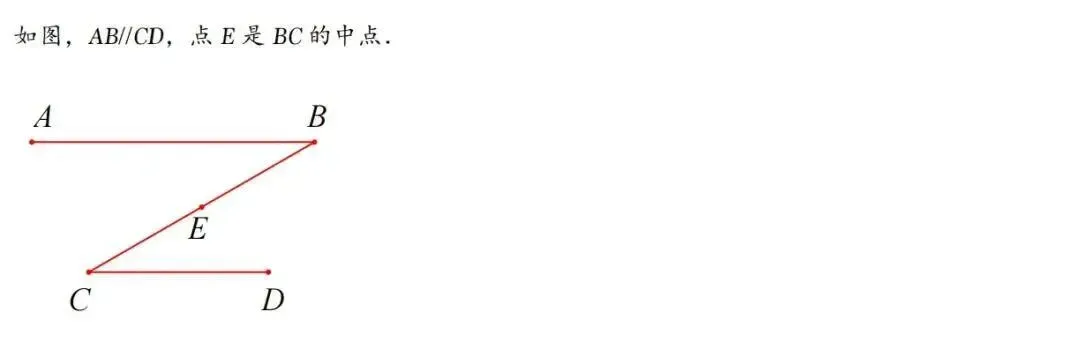
2、历史文章

一题多解｜截长补短问题6种证明方法

八、绝配角模型

1、基本模型‍‍‍

2、结论推导

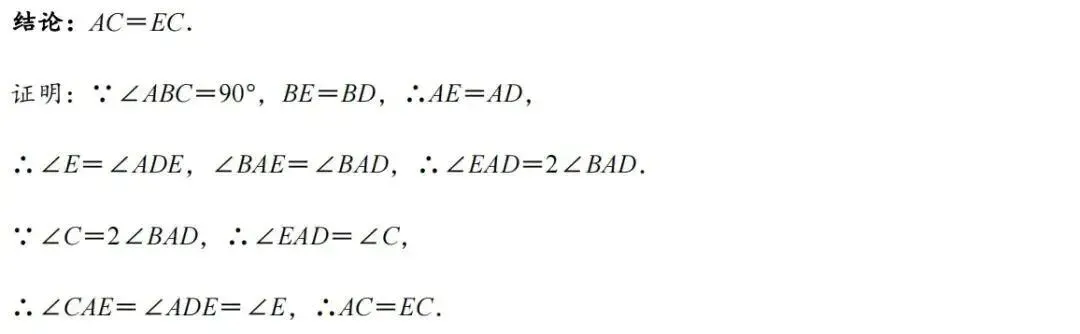
3、解题技巧

如果题目中出现二倍角，可以考虑用绝配角模型，构造等腰三角形，绝配角＋等腰三角形＋全等三角形一般同时出现，然后用勾股定理或相似求解．构造等腰三角形是这类绝配角问题的重要方法．

4、历史文章

来解题吧 | 绝配角在几何解题中的应用

九、婆罗摩笈多模型

‍‍

1、基本模型

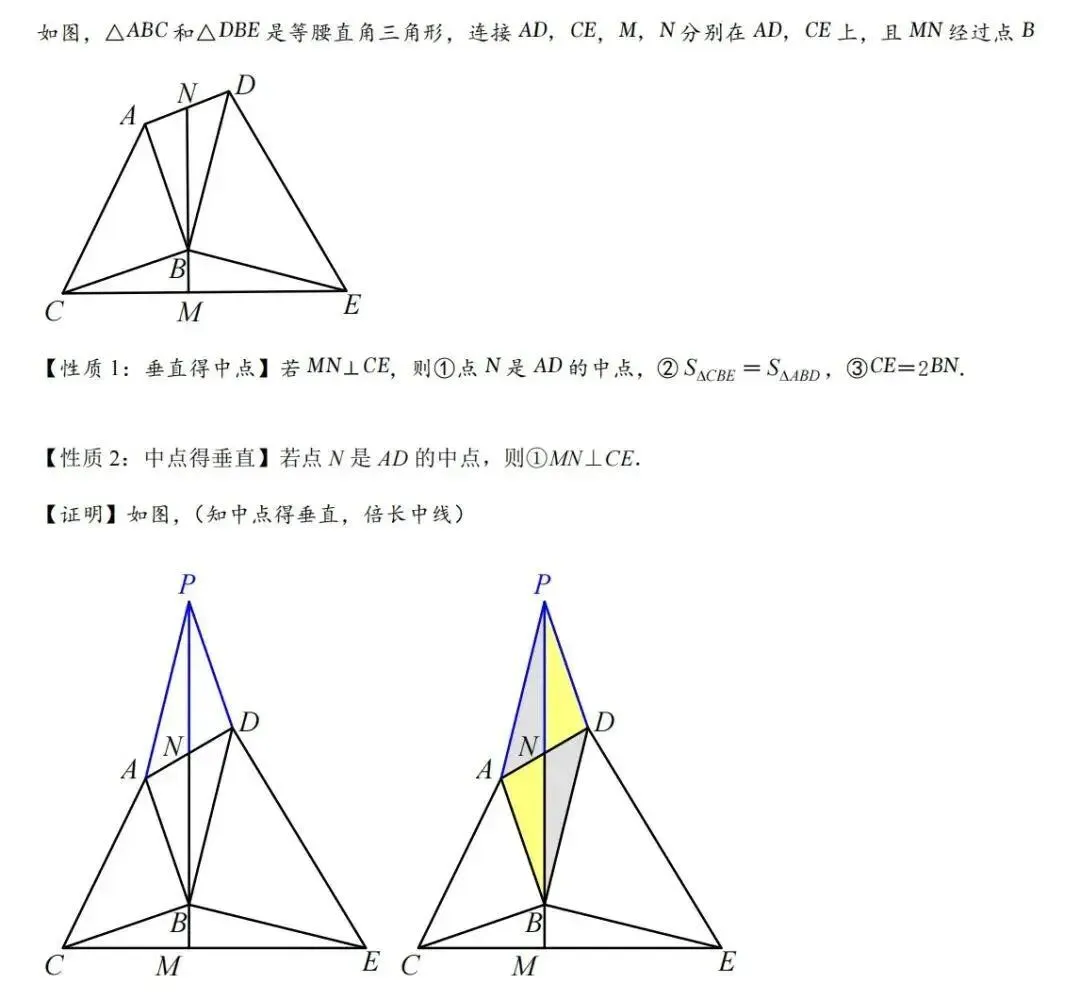
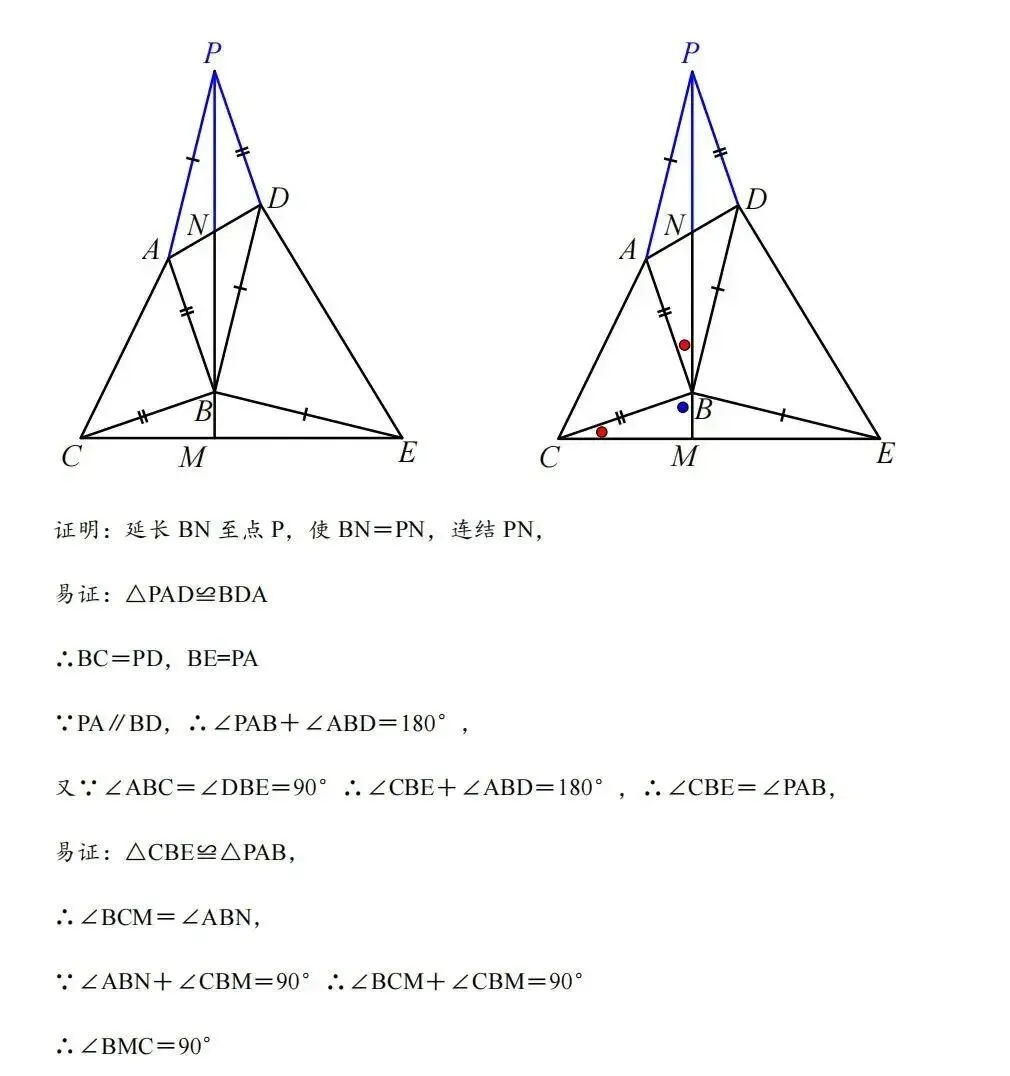
2、历史文章

几何模型 | 婆罗摩笈多定理&模型&公式

十、海岛埋宝模型

1、基本模型

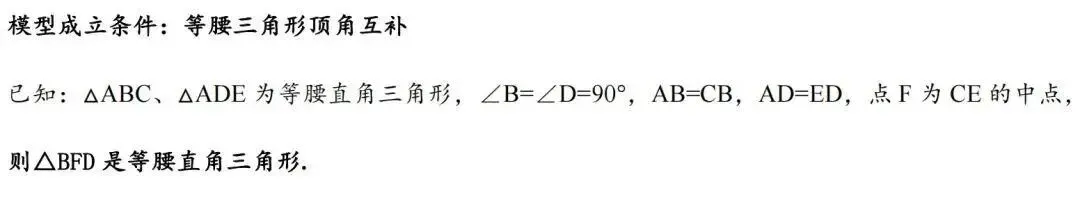
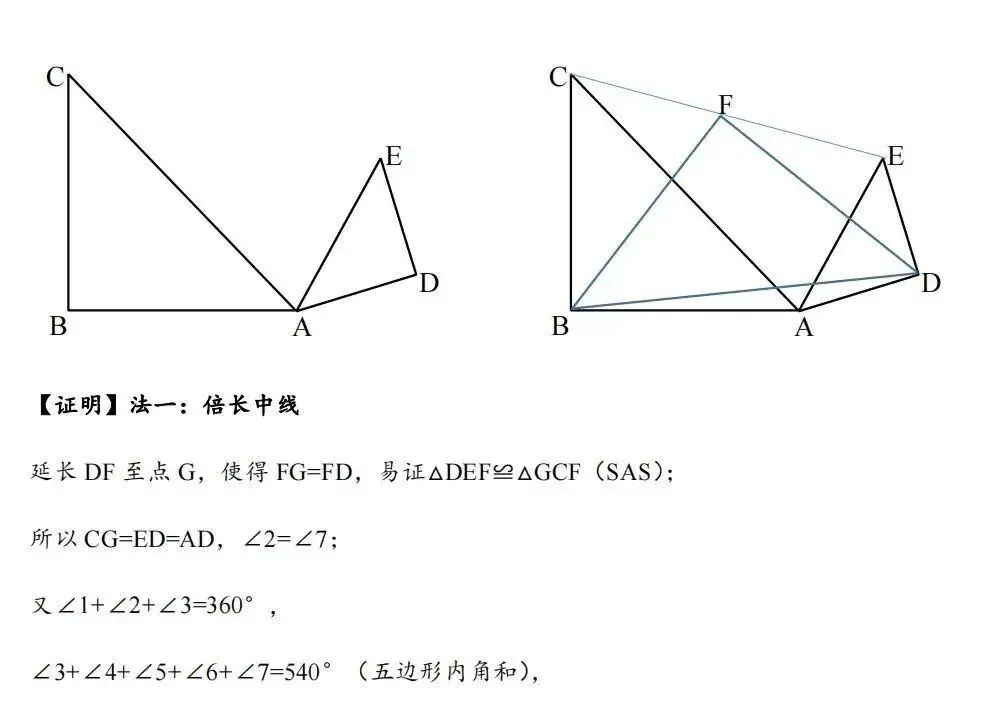
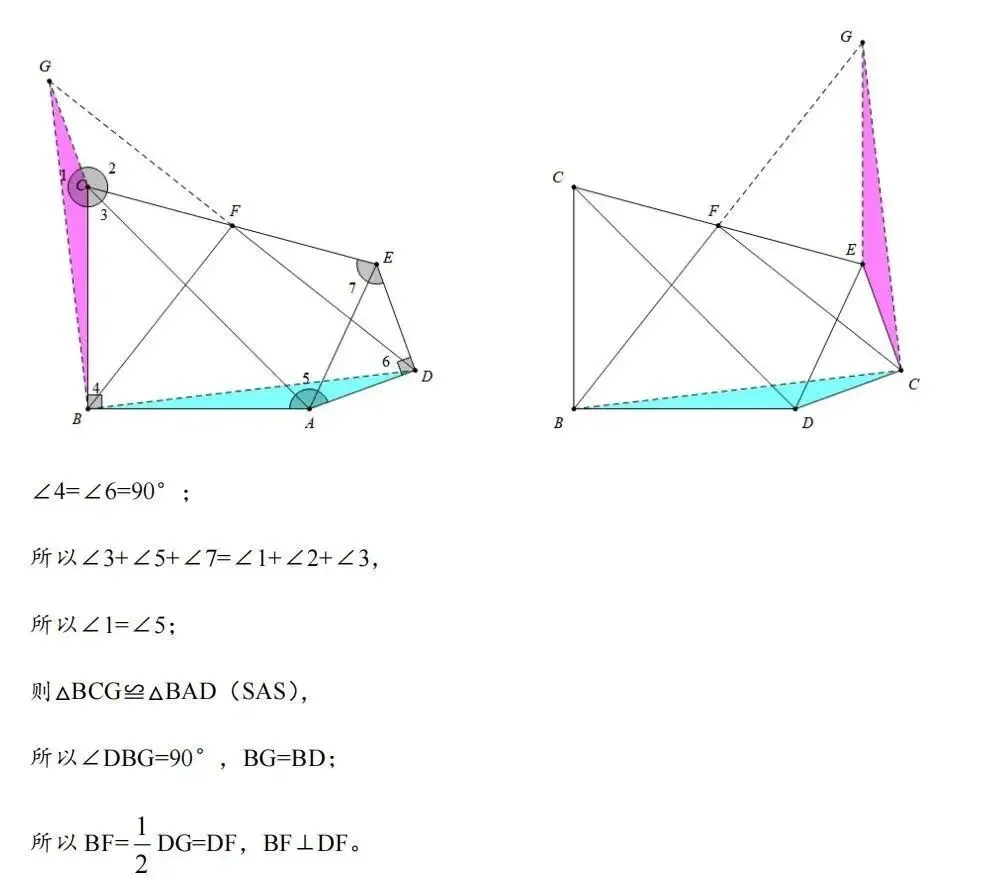
2、历史文章‍‍‍‍

趣味几何｜海盗埋宝&婆罗摩笈多

趣味几何｜当三角形长出一对耳朵