(51)2025年河南中考
漯河市一模数学第23题
综合与实践
在学习特殊四边形的过程中,我们积累
了一定的研究经验,请运用已有的经验,
对"勾股四边形"进行研究.
定义:存在相邻两边的平方和等于其中
一条对角线的平方的四边形叫做"勾股
四边形",这两条相邻的边称为这个
四边形的勾股边.
特例感知
(1)在平行四边形,矩形,菱形,
正方形四种图形中,一定为"勾股
四边形"的是________________,
性质探究
(2)如图1, OA=OB , OC=OD ,
∠AOB=∠COD=2θ,∠BDO=θ,
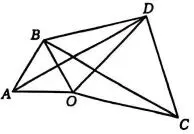
图1
①求证:无论θ取何值,四边形OBDC
一定为"勾股四边形".
拓展应用
②若四边形ABDO也为"勾股四边形",
且BD , OD为勾股边,求θ的值,
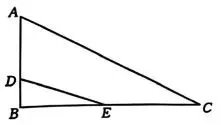
图2
(3)如图2,在Rt△ABC中,∠B=90°,
AB=3, BC=6, D是边AB的三等分点
(BD<AD), E是边BC的中点,在边AC
上取一点F,使得四边形ADEF是"勾股
四边形",当DE和EF是勾股边时,
请直接写出 CF 的长.
【解析】(1)矩形、正方形 ,
(2)①∵OC=OD , ∠COD=2θ,
∴∠ODC=∠OCD
=(180°-∠COD)/2
=(180°-2θ)/2
=90°-θ,
又∵∠BDO=θ,
∴∠BDC=∠BDO+∠ODC
=90°,
在 Rt△DCB中,
DC²+BD²=BC²,
即四边形OBDC一定为"勾股四边形",
②∵∠AOB=∠COD=2θ,
∴∠AOD=∠BOC ,
在△AOD与△BOC中,
∵OA=OB ,
∠AOD=∠BOC ,
OD=OC ,
∴△AODS≌△BOC (SAS),
∴AD=BC ,
又∵DC²+BD²=BC² ,
∴DC²+BD²=AD²,
∵四边形ABDO为"勾股四边形",
且 OD²+BD²= AD² ,
∴ CD=OD ,
又∵OC=OD ,
∴△DOC是等边三角形,
∴∠COD=2θ=60°,
∴θ=30°,
⑶ 9√5/7
或 (6√5+√155)/5
或 (6√5-√155)/5,
∵ AB=3,
D是边AB的三等分点(BD<AD),
∴AD=2, BD=1,
∵BC=6,
E是边BC的中点,
∴BE=CE=3,
∴AE=3√2,DE=√10,AC=3√5,
分两种情况:
①当DE²+EF²=DF²,
即∠DEF=90°,
如图3,过点F作FG⊥BC于点G,
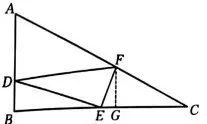
图3
易得△ACB∽△FCG ,
△DBE∽△EGF ,
∴CG/FG=BC/AB
=6/3
=2,
EG/FG=BD/BE
=1/3,
∴CG=2FG, EG=1/3FG ,
∴CG=6EG,
∵CE=3,
∴CG=6/7CE=18/7,
∴FG=9/7,
∴CF=9√5/7,
②DE²+ EF²=AE²,
即(√10)²+EF²=(3√2)²,
解得 EF=2√2,
如图4、图5,分别过点E作EH⊥AC
于点H ,
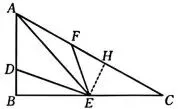
图4
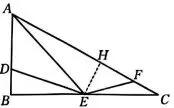
图5
易得△ACB∽△ECH ,
∴CH/CB=EH/AB
=CE/CA
=3/(3√5)
=√5/5,
∴EH=3√5/5,
CH=6√5/5,
∵EF=2√2,
∴HF=√155/5,
∴CF=CH±HF
=(6√5±√155)/5,
综上所述, CF的长为9√5/7
或(6√5+√155)/5
或 (6√5-√155)/5,
往期文章






