钱金山|中考数学跨学科试题归类解析

中考数学跨学科试题归类解析

钱金山

摘要：数学跨学科试题是指以数学学科内容为核心，融合其他学科知识、思想、方法的试题.纵观近几年各地的中考试题，数学逐步趋于生活化、应用化，学科间知识联系增强，注重考查知识的应用及解决实际问题的能力.通过分类解析全国部分地区近几年中考数学试题中涉及的跨学科案例，探讨这些案例对初中数学教学带来的启示.

关键词：中考数学跨学科试题解题方法

数学是研究数量关系和空间形式的科学，源自人们对现实世界的抽象.世界在发展，科技在进步，仅凭单一学科知识结构难以解释复杂的现实问题，因此，跨学科试题研究应运而生.《义务教育数学课程标准(2022年版)》(下称“新课标”)与之前各版本相比，增设占课程总课时不少于10%的跨学科主题学习是其亮点之一，包括以“综合与实践”为基础“设立跨学科主题学习活动，加强学科间相互关联，带动课程综合化实施，强化实践性 要求”[1].

跨学科试题的命制是中考命题领域长期探索的热门话题，以期通过中考试题的“指挥棒”作用，引导教师积极探索基于试题情境、深度思维、融合度高的跨学科试题.下面，通过对近几年部分地区中考数学试卷中跨学科试题进行分类与解析，分析跨学科试题融合的类型及考查的形式，以期加深对跨学科试题的理解，提升数学的应用价值[2].

1 试题呈现

1.1 与语文联手

例1 (2024年吉林省)图1中有一首古算诗，根据诗中的描述可以计算出红莲所在位置的湖水深度，其示意图如图2,其中AB=AB′, AB⊥B′C于点C,BC=0.5尺，B′C=2尺.设AC的长度为x尺，可列方程为______.

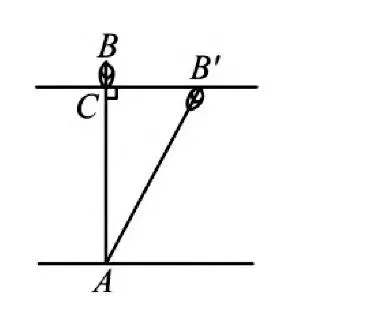
解析 由诗句中的描述，得AB=AB′=x+0.5,又AB⊥B′C,由勾股定理得AC²+B′C²=AB′²,即x²+2²=(x+0.5)².

点评 本题以古诗句为背景引出一个实际问题，要求考生根据题目描述，结合示意图，用勾股定理建立关于湖水深度的一元二次方程.试题考查了考生对勾股定理的理解和应用能力，以及将实际问题抽象为数学模型的能力.学生的数学知识和技能、数学建模、空间想象、解决问题的能力都得到了测试.该题有助于全面评估学生的数学素养，促进其全面发展.

1.2 与物理串联

例2 (2024年河南省)把多个用电器连接在同一个插线板上，同时使用一段时间后，插线板的电源线会明显发热，存在安全隐患.数学兴趣小组对这种现象进行研究，得到时长一定时，插线板电源线中的电流I与使用电器的总功率P的函数图象(图3)、插线板电源线产生的热量Q与I的函数图象(图4).下列结论中错误的是( ).

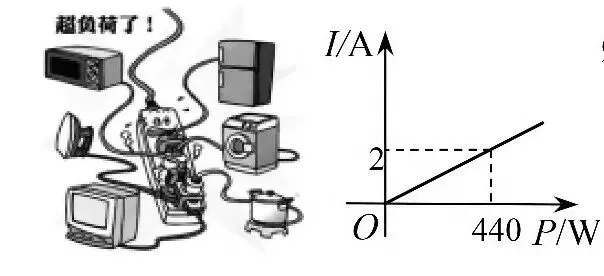
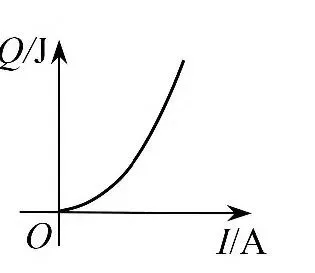
A.当P=440 W时，I=2 A

B.Q随I的增大而增大

C.I每增加1 A,Q的增加量相同

D.P越大，插线板电源线产生的热量Q越多

解析 根据图3知，当P=440 W时，I= 2 A,故选项A正确；根据图4知，Q随I的增大而增大，但前小半段增加的幅度小，后面增加的幅度大，故选项B正确、选项C错误；根据图3知，I随P的增大而增大，由图4可知，Q随I的增大而增大，故P越大，插线板电源线产生的热量Q越多，选项D正确.故选C.

点评 本题以插线板电源线发热为背景，理解函数图象是解题的关键.试题考查了学生的数学建模和逻辑推理能力，体现了数学与物理的跨学科融合，考生需要具备综合运用多学科知识解决问题的能力.

1.3 与化学反应

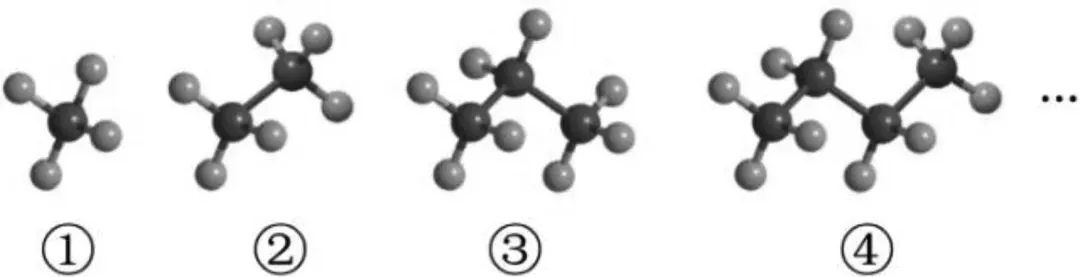
例3 (2024年重庆市)烷烃是一类由碳、氢元素组成的有机化合物质，图5是这类物质前四种化合物的分子结构模型图，其中灰球代表碳原子，白球代表氢原子.第1种如图5①有4个氢原子，第2种如图5②有6个氢原子，第3种如图5③有8个氢原子，……按照这一规律，第10种化合物的分子结构模型中氢原子的个数是( ).

A.20 B.22 C.24 D.26

解析 由图5可得，第1种有4个氢原子，即2+2×1=4,第2种有6个氢原子，即2+2×2=6,第3种有8个氢原子，即2+2×3=8,……因此第10种化合物的分子结构模型中氢原子的个数是2+2×10=22,故选B.

点评 本题是一道找规律的题目，通过给出烷烃类化合物前四种的分子结构模型图，要求考生找出氢原子个数的变化规律，并利用数列知识求解第10种化合物的分子结构模型中氢原子的个数.该题考查了观察能力、分析能力和代数运算能力，体现了数学与化学的跨学科融合，要求考生能够运用数学知识解决化学问题.

1.4 与时政挂钩

例4 (2024年江苏省宿迁市)全国两会期间，习近平总书记在参加江苏代表团审议时指出，我们能不能如期全面建成社会主义现代化强国，关键看科技自立自强.将“科技、自立、自强”六个字分别写在某正方体的表面上，如图6是它的一种表面展开图，在原正方体中，与“强”字所在面相对面上的汉字是( ).

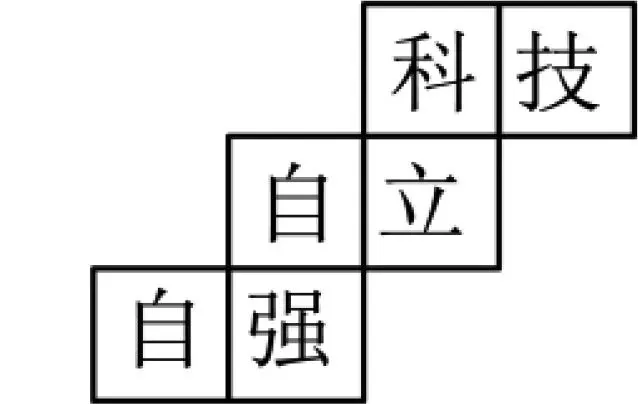
A.自 B.立

C.科 D.技

解析 将中间的“自”作为底面，则折起来“强”在前面，“立”在右面，“科”在后面，故与“强”字所在面相对面上的汉字是“科”,故选C.

点评 本题以全国两会为背景，给出一个正方体的表面展开图，要求考生判断原正方体中与“强”字所在面相对面上的汉字，考查考生的空间想象力和逻辑推理能力.解题的关键在于理解正方体表面展开图与原正方体之间的对应关系，并据此进行逻辑推理，对考生的空间思维和推理能力都有一定要求.

1.5 与地理同行

例5 (2022年贵州省遵义市)数学小组研究如下问题：遵义市某地的纬度约为北纬28°,求北纬28°纬线的长度.小组成员查阅相关资料，得到如下信息：

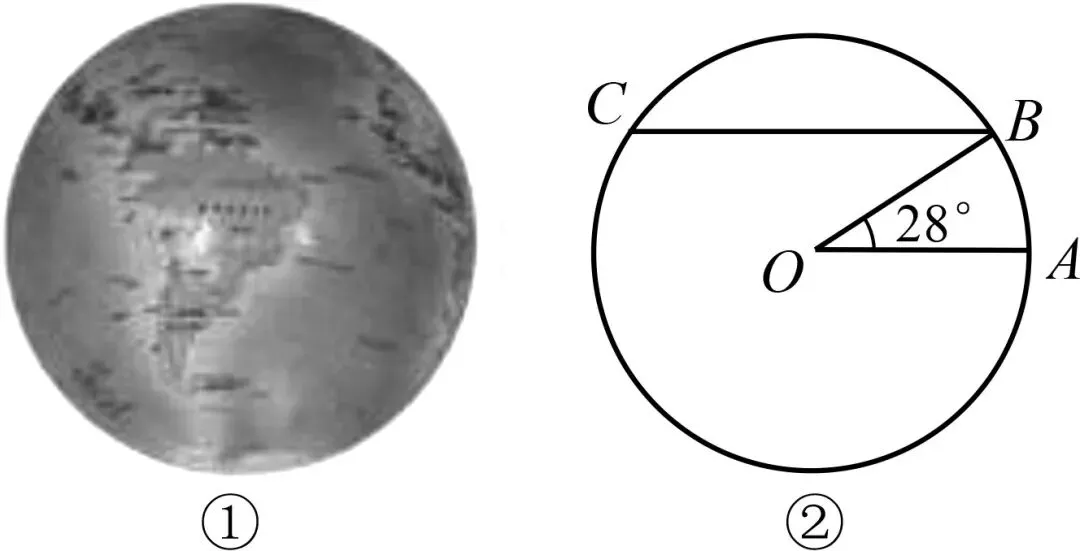
信息一：如图7①,在地球仪上，与赤道平行的圆圈叫作纬线.

信息二：如图7②,赤道半径OA约为6 400千米，弦BC∥OA,以BC为直径的圆的周长就是北纬28°纬线的长度.

(参考数据：π≈3,sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53)

根据以上信息，北纬28°纬线的长度约为______千米.

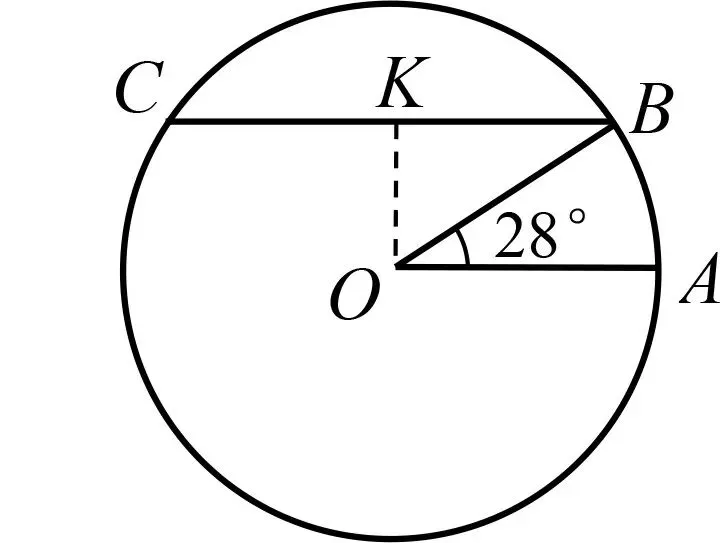
解析 如图8,过O作OK⊥BC,则∠BKO=90°,由BC//OA,∠AOB=28°,知∠B=∠AOB=28°.

在Rt△BOK中，OB=OA= 6 400,于是BK=OB× cos ∠B≈6 400×0.88=5 632,故北纬28°的纬线长=2π·BK≈2×3×5 632=33 792(千米).答案为33 792.

点评 本题以地理中纬线为背景，结合数学中的垂径定理、解直角三角形、三角函数的含义及解直角三角形的方法，抽象出纯粹的数学问题加以解决，初步彰显跨学科思维的价值，体现数学学科应用的广泛性.

1.6 与生物交融

例6 (2022年湖北省鄂州市)生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型.在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2ⁿ来表示，即：2¹=2,2²=4,2³=8,2⁴=16,2⁵=32,…,请你推算2^{2 022}的个位数字是( ).

A.8 B.6 C.4 D.2

解析 由2¹=2,2²=4,2³=8,2⁴=16,2⁵=32,…,发现尾数每4个一循环，因为2 022÷4=505……2,所以2^{2 022}的个位数字应该是4,故选C.

点评 本题选用生物学中的细胞分裂繁殖现象作为背景，通过题干发现数字变化规律是解题关键，考查跨学科综合能力和应用能力.这种跨学科的题目有助于培养考生的综合素质和创新能力，也是未来评价性测试的一个重要趋势.

1.7 与信息技术共赢

例7 (2023年江苏省常州市)如图9,小红家购置了一台圆形自动扫地机，放置在屋子角落(书柜、衣柜与地面均无缝隙).在没有障碍物阻挡的前提下，扫地机能自动从底座脱离后打扫全屋地面.若这台扫地机能从角落自由进出，则图9中的x至少为______.(精确到个位，参考数据：)

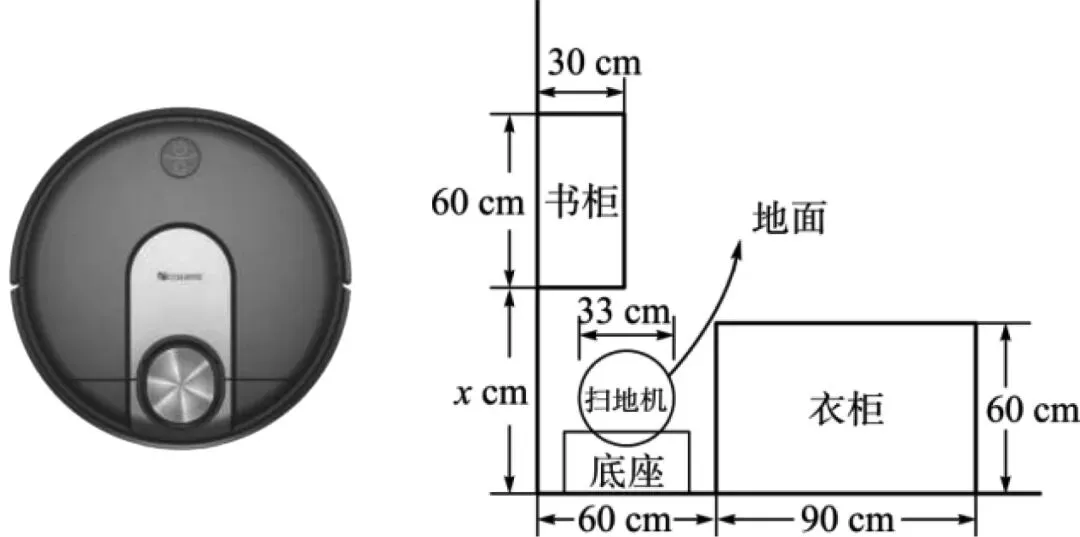
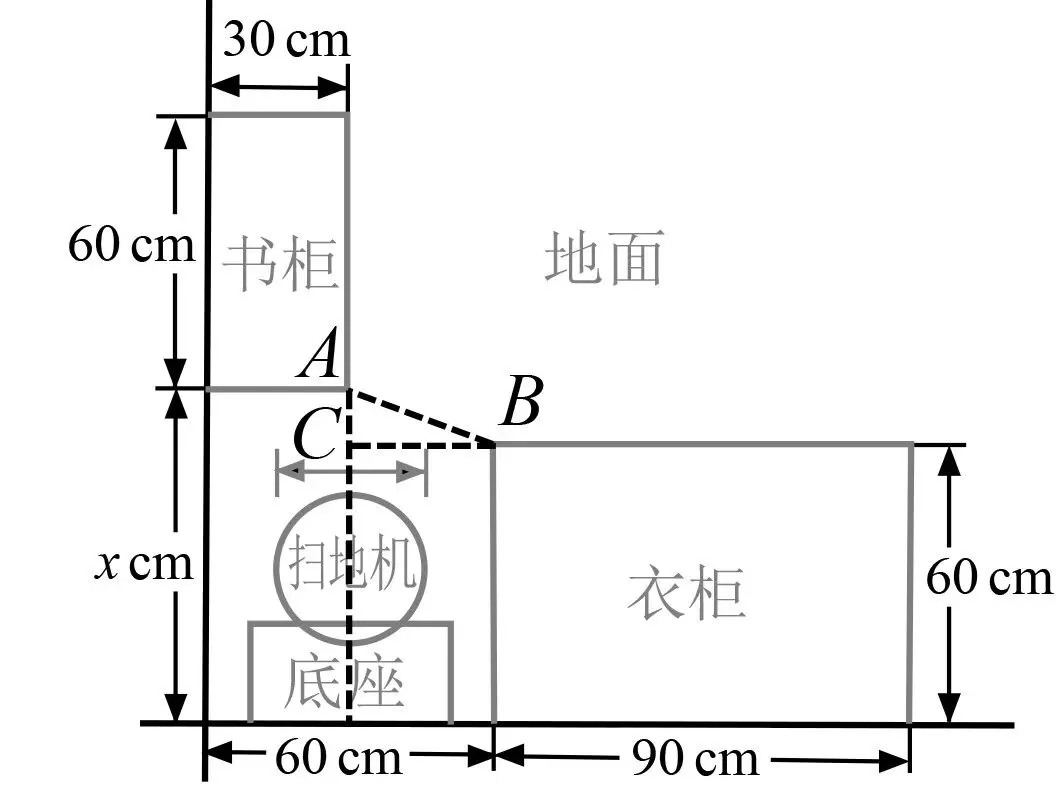
解析 如图10,过点A,B分别作墙的垂线，交于点C,则AC=(x-60) cm, BC=60-30= 30 cm.在Rt△ABC中，AC²+BC²=AB²,即(x-60)²+30²=AB².

想让这台扫地机能从角落自由进出，则这台扫地机的直径不大于AB长，即AB最小满足(x-60)²+30²=33²,解得,因此图中的x至少为74 cm.

点评 本题从人工智能与数学关系的角度，展示了扫地机运动规划中的数学原理和应用.学生可以通过分析和求解这个问题，体会数学在人工智能领域的重要性.这提醒教师在教学时要注重跨学科的学习和融合，以更好地应对复杂多变的问题和挑战.

1.8 与体育竞技

例8 (2023年江苏省常州市)折返跑是一种跑步的形式.如图11,在一定距离的两个标志物①、②之间，从①开始，沿直线跑至②处，用手碰到②后立即转身沿直线跑至①处，用手碰到①后继续转身跑至②处，循环进行，全程无需绕过标志物.小华练习了一次2×50 m的折返跑，用时18 s, 在整个过程中，他的速度大小v(m/s)随时间t(s)变化的图象可能是( ).

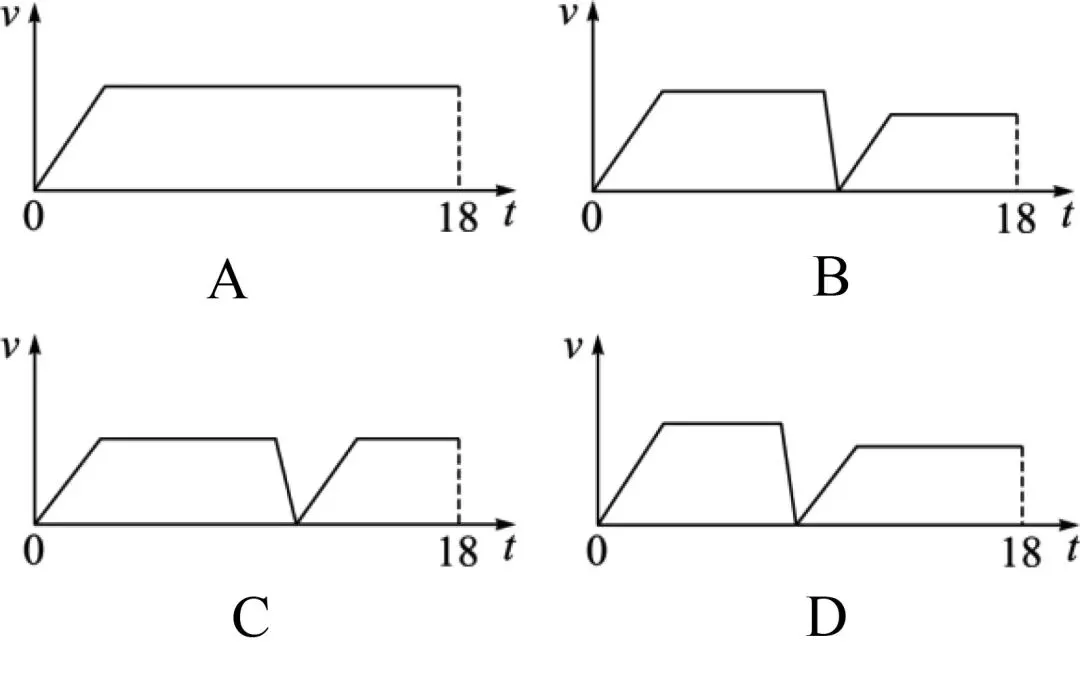
解析 刚开始速度随时间的增加而增大，匀速跑一段时间后减速，到达②,然后再加速后匀速到达①,由于体力原因，应该第一个50米速度快、用时短，第二个50米速度慢、用时长，故小华的速度v随时间t变化的图象可能是D.

点评 本题主要考查函数图象的性质，分析函数的类型和所需要的条件，结合实际意义得出正确的结论.该题体现了数学与体育之间的紧密融合、数学在体育领域中的广泛应用，以及体育对数学学习的促进作用.

2 教学启示

2.1 跨学科试题在考查内容上各有其重点和特色

纵观近几年全国部分地区中考涉及跨学科情境的试题分布，可以发现它们主要聚焦于三种题型：单项选择题、填空题以及解答题.这三种题型在跨学科情境的呈现上各有侧重，对考生的能力要求也各具特点.单项选择题倾向于检验学生对数学基础概念的掌握与理解；填空题考查数学概念，要求学生能对数量关系进行初步的分析与判断；解答题更加注重在跨学科问题中的综合应用与分析能力，鼓励学生运用多学科知识深入探究并解决问题[3].

2.2 注重情境问题的设置

在跨学科试题情境的构建中，为了确保能够准确评估学生的综合能力与实践能力，问题任务的设计显得尤为关键.设计问题时，需紧密结合情境背景，精心调配问题任务、必备知识技能以及情境条件之间的契合程度，以保证问题任务与真实情境之间的高度相关性.此外，还应重视问题任务设置的科学性、合理性、相关性和过程性，从而确保评估的全面性和有效性.

2.3 创新教学方式

为适应跨学科命题的新要求，教师应当积极革新教学方法，引入项目式学习和单元教学等新型教学模式，以激发学生的学习兴趣，拓宽思维视野.通过这些学习活动，学生能够在实际问题的解决过程中灵活融合各科知识，提升其解决问题的能力，培养“四能”、发展“三会”,提高学生的综合能力.这也为高中阶段教育模式的转型奠定坚实的义务教育基础，对于学生未来的学习和生活都具有重要意义.

参考文献

• [1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022:前言4.

• [2]尹国益.跨学科数学试题分类及解析——以2024年中考题为例[J].初中数学教与学,2024(21):37-40.

• [3]孙虎,张维忠.2023年中考数学试题中的跨学科问题[J].中学数学教学参考,2024(20):59-62.