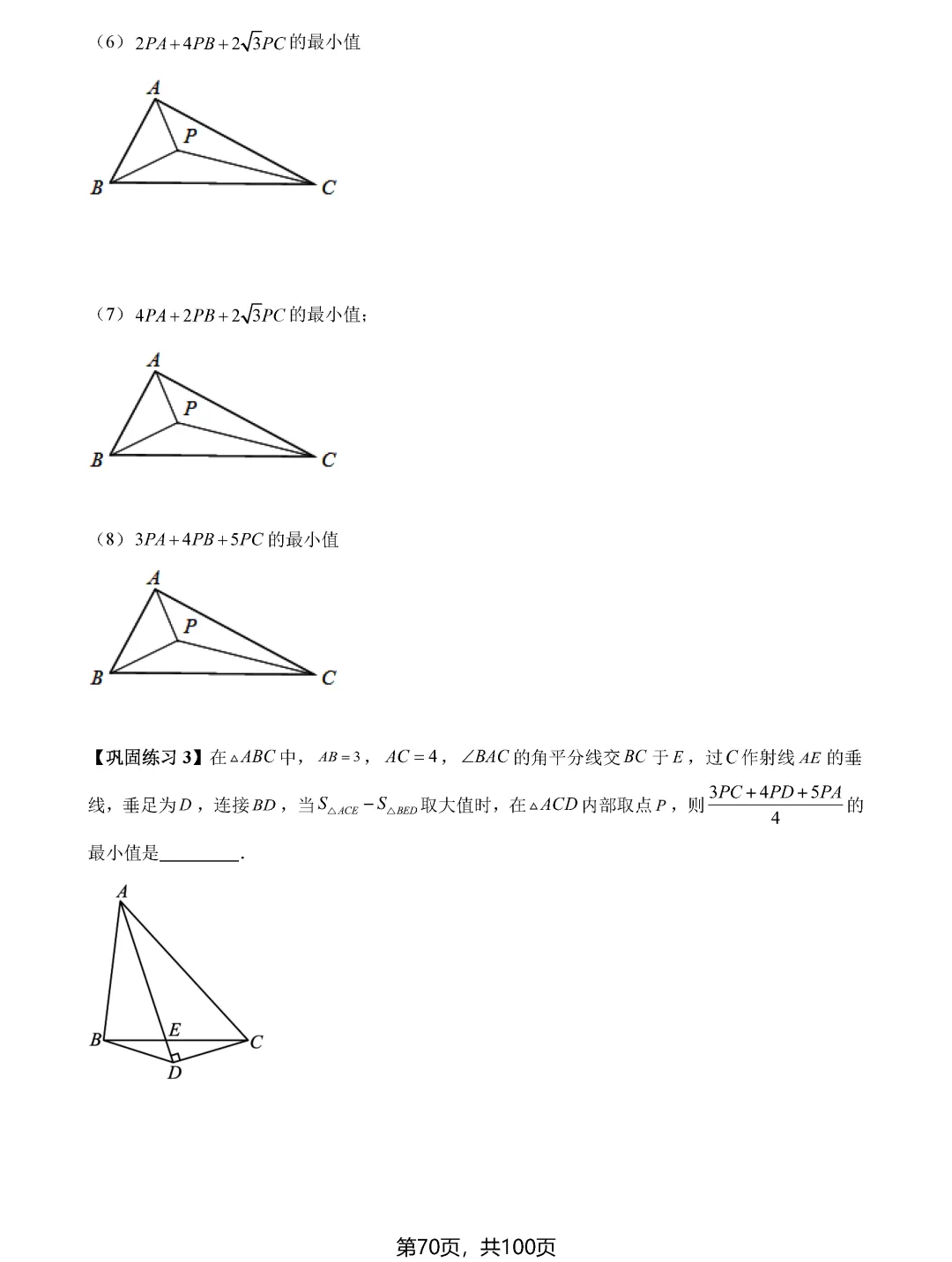
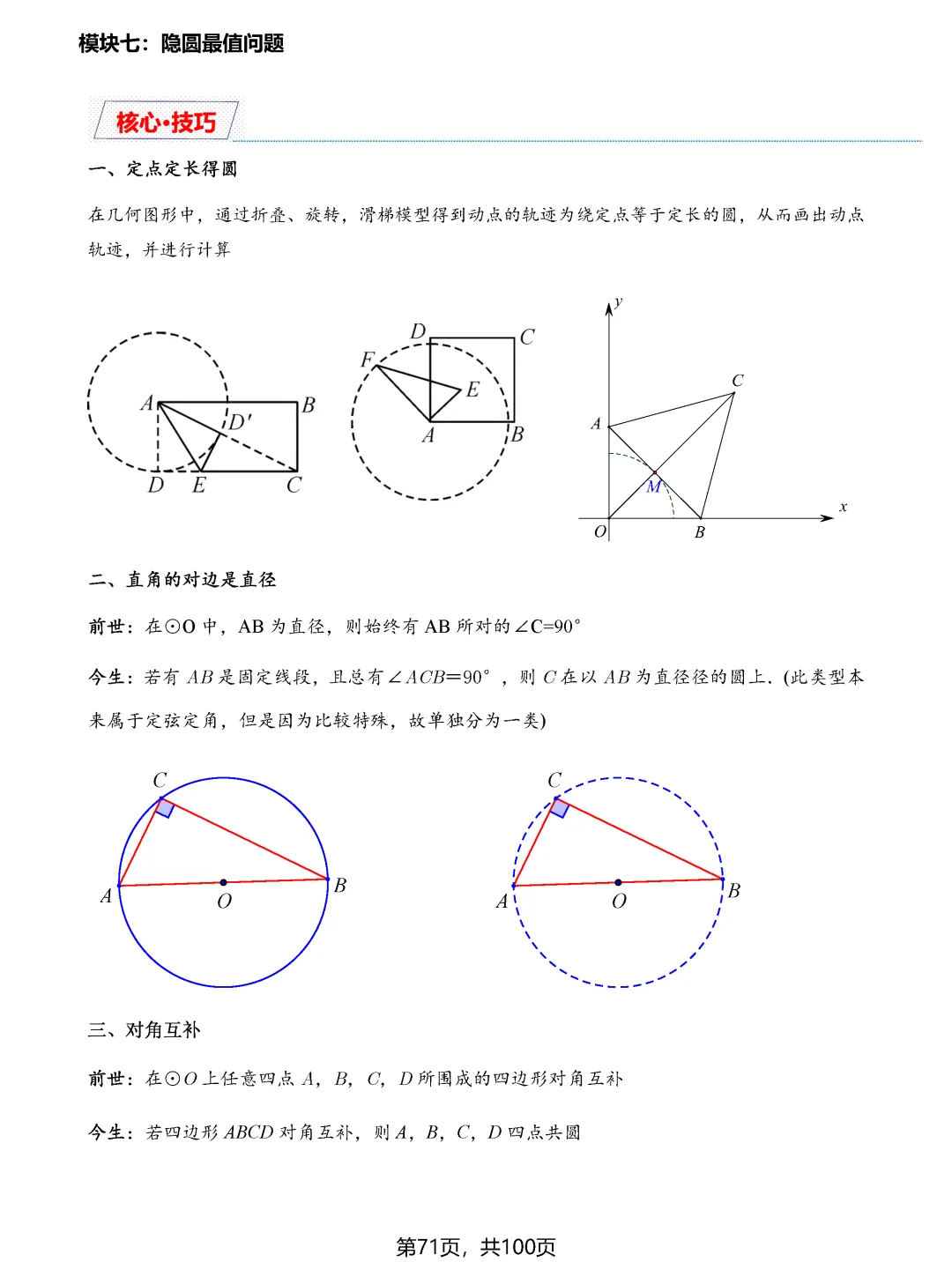
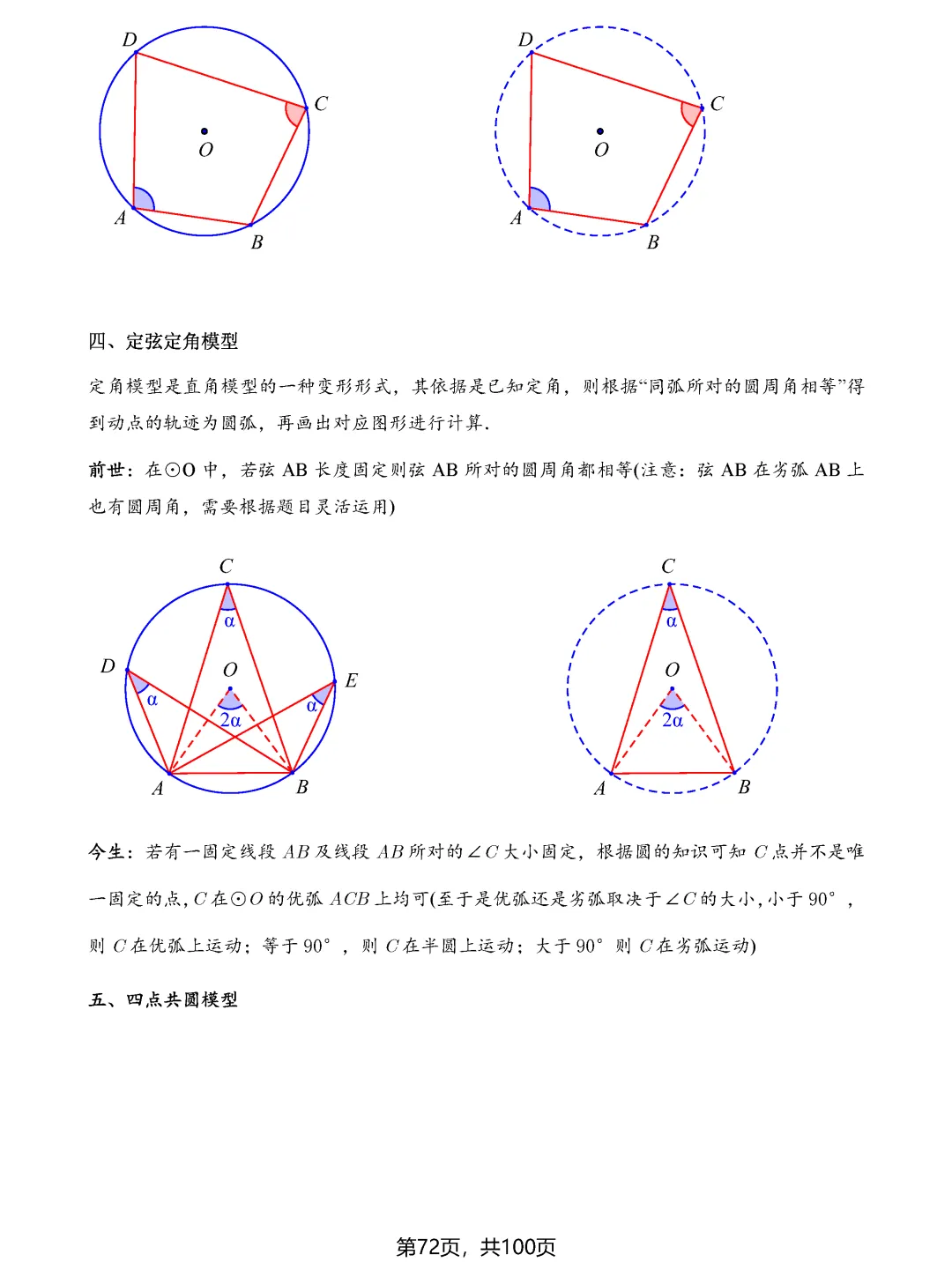
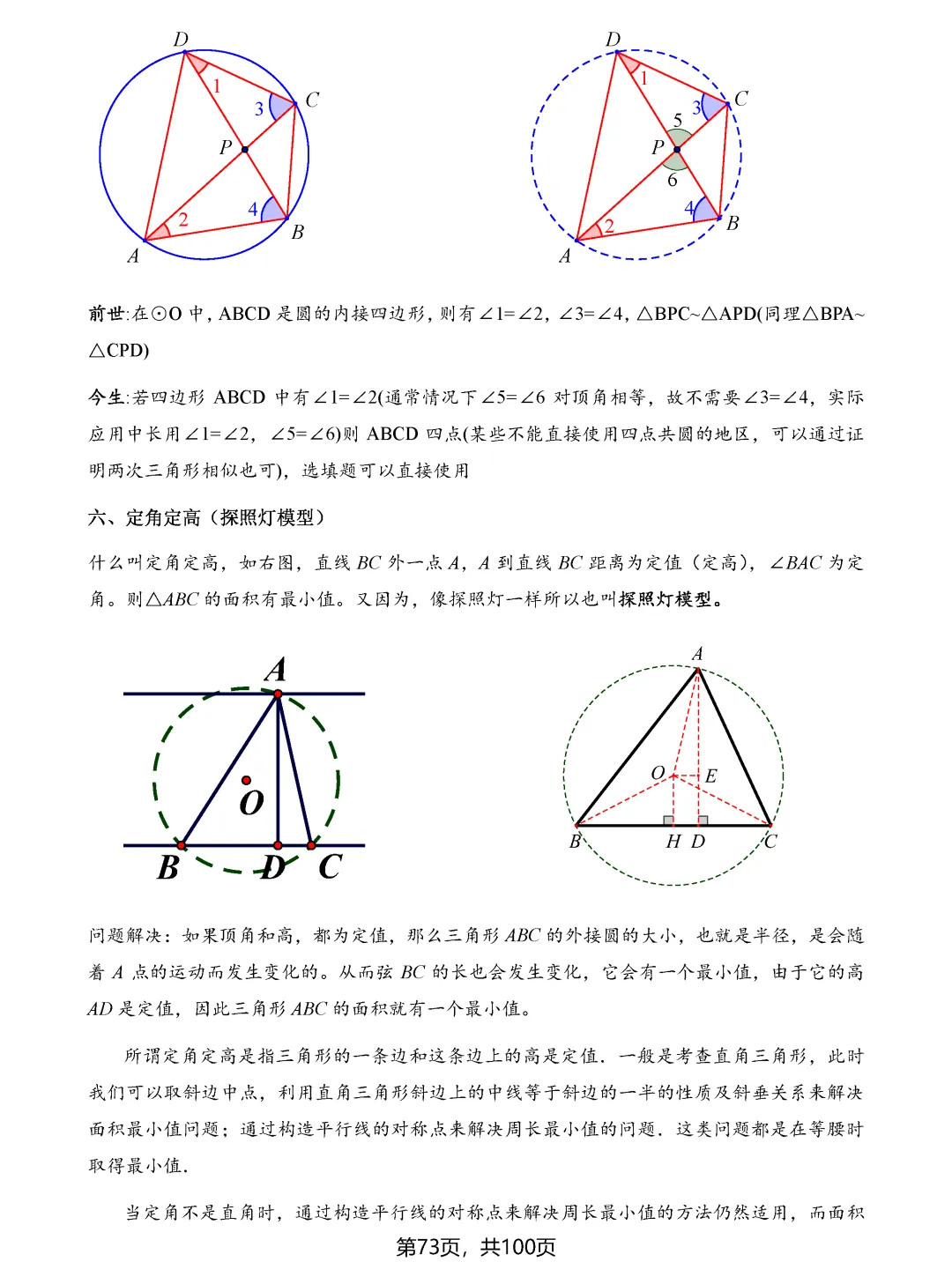
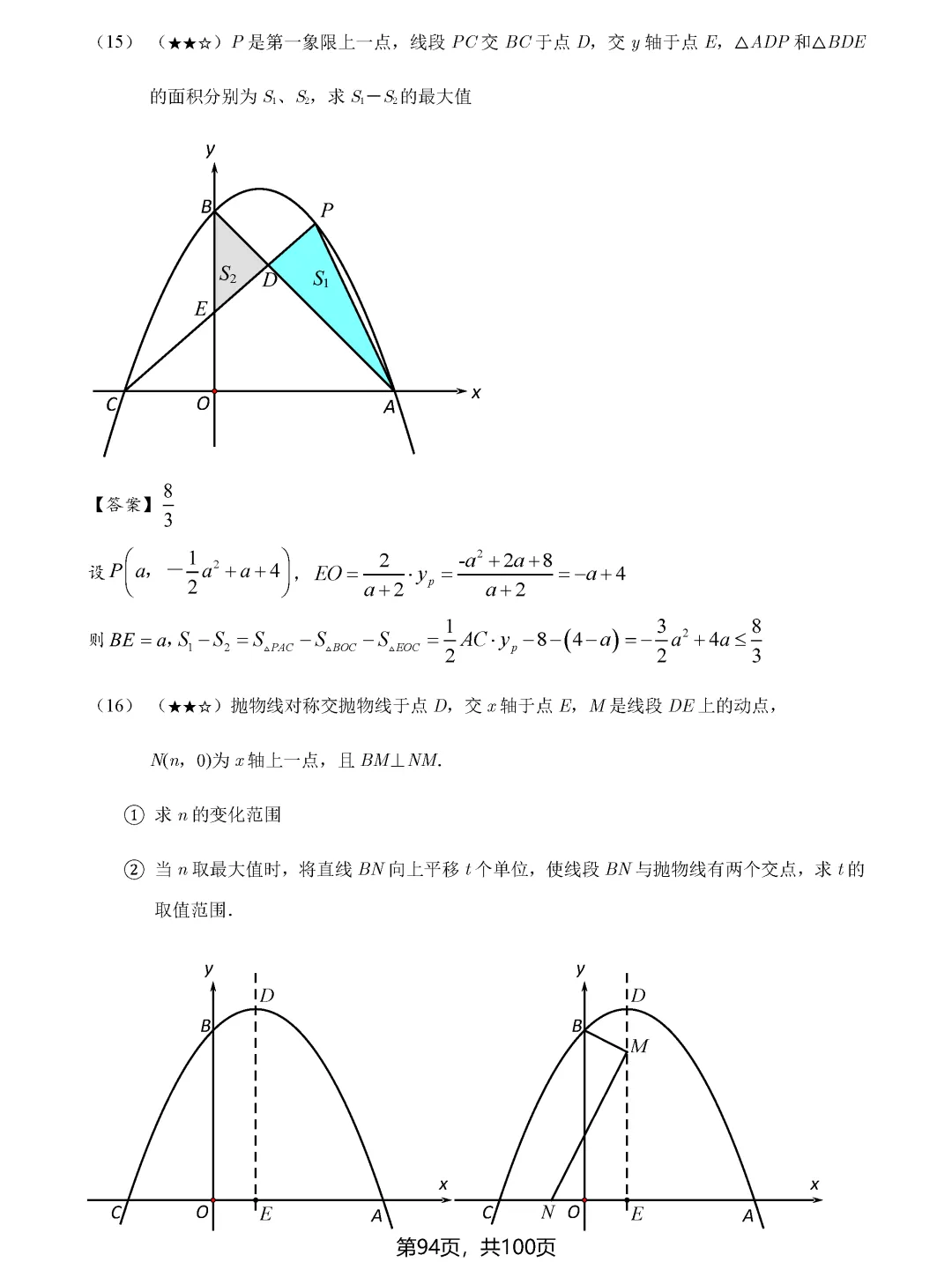
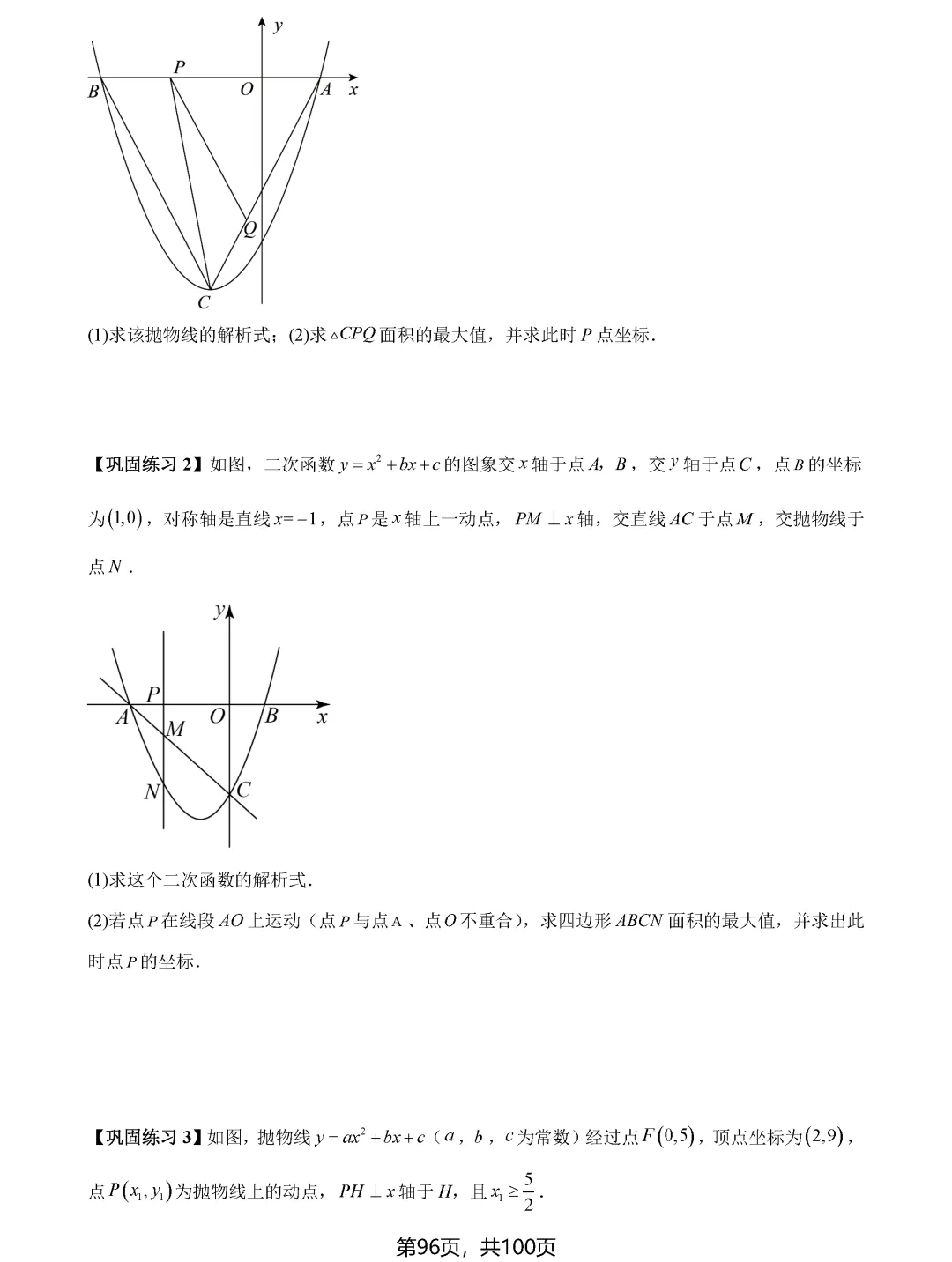
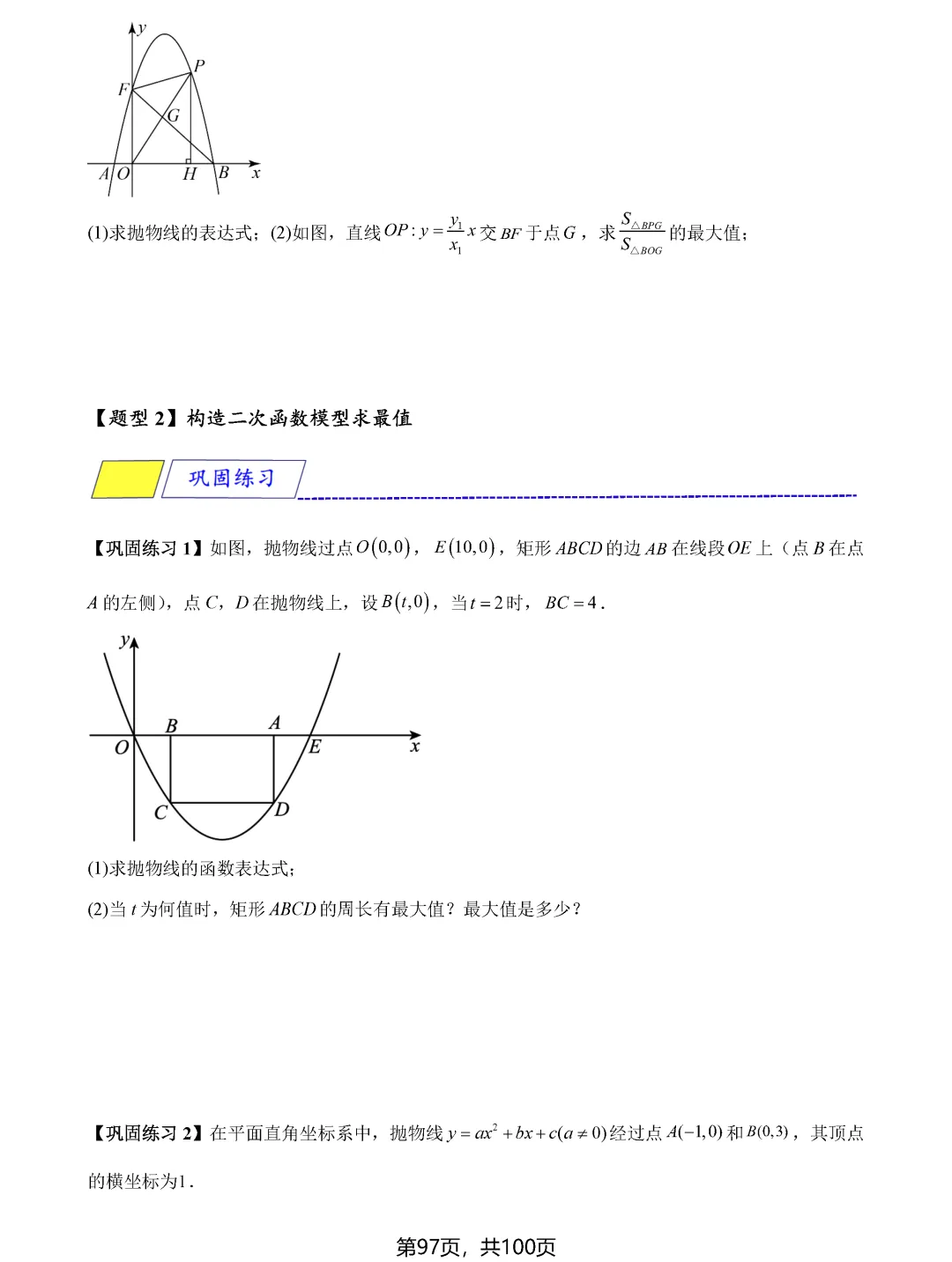
中考数学最值问题一直是压轴题中的重头戏,也是拉开分数差距的关键所在。面对这类题目,许多同学感到无从下手,其实最值问题虽然变化多端,但核心模型和解题思路是有规律可循的。掌握这八大类最值问题的解题技巧,能够帮助同学们在中考中稳拿高分。
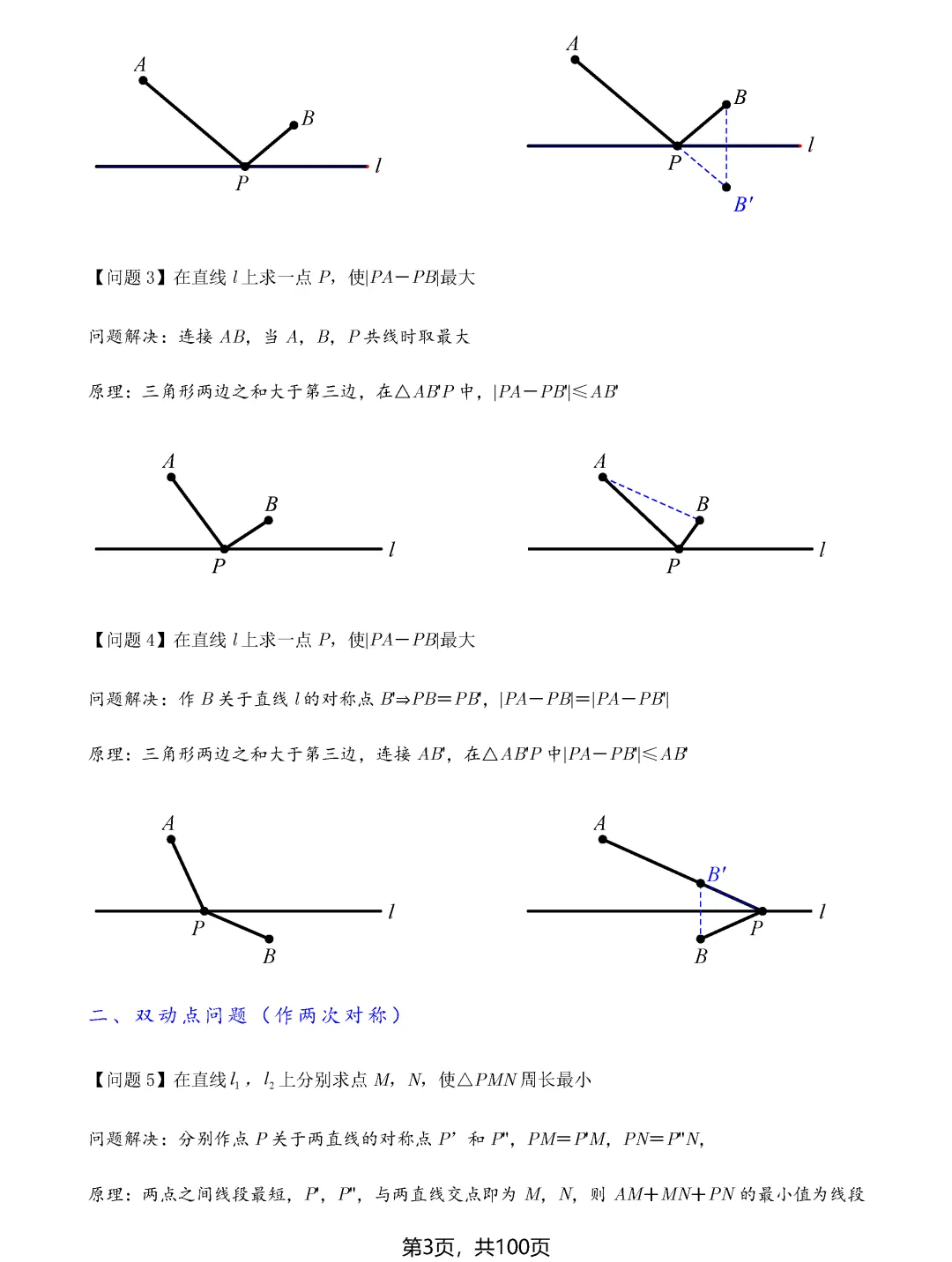
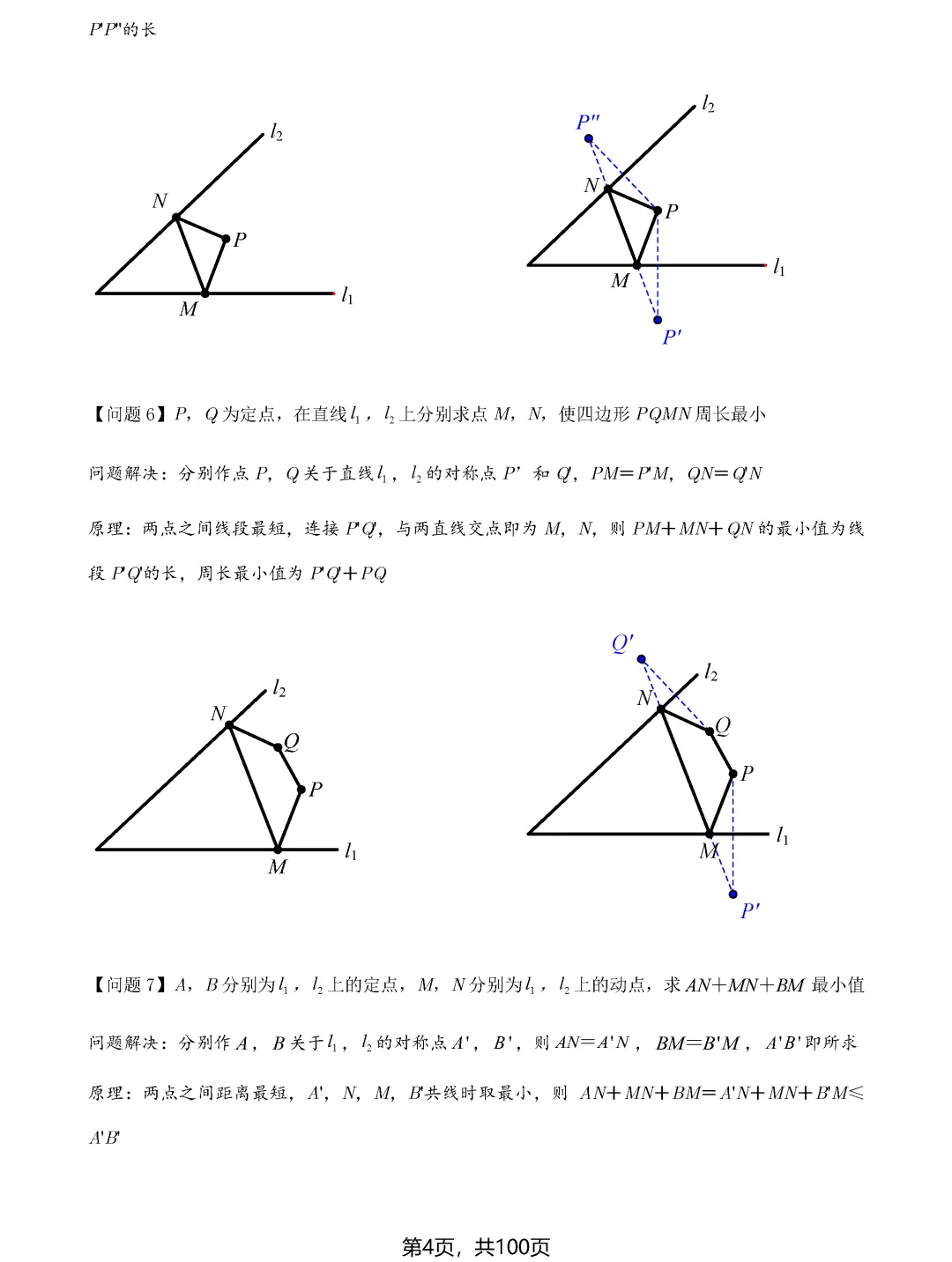
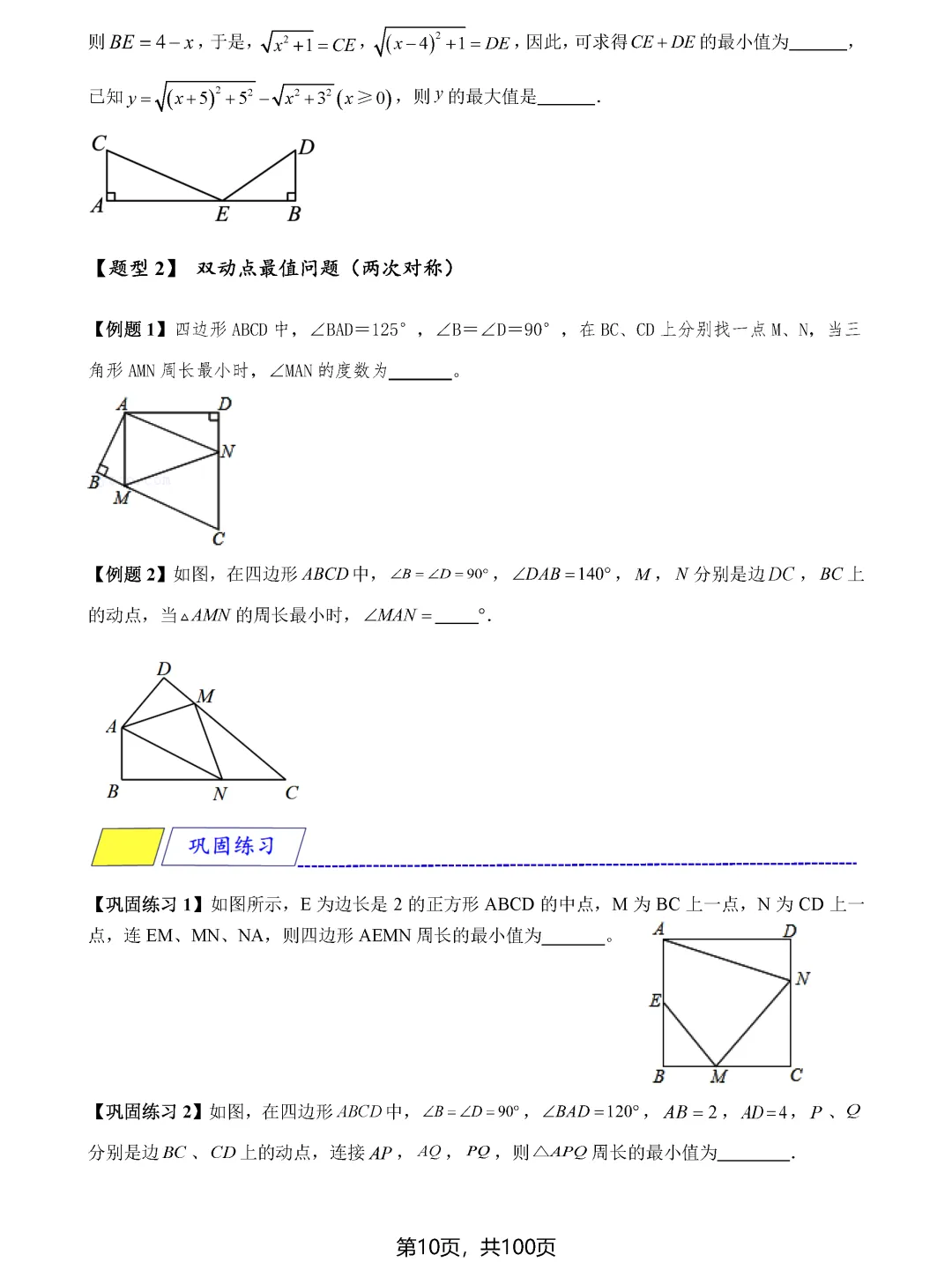
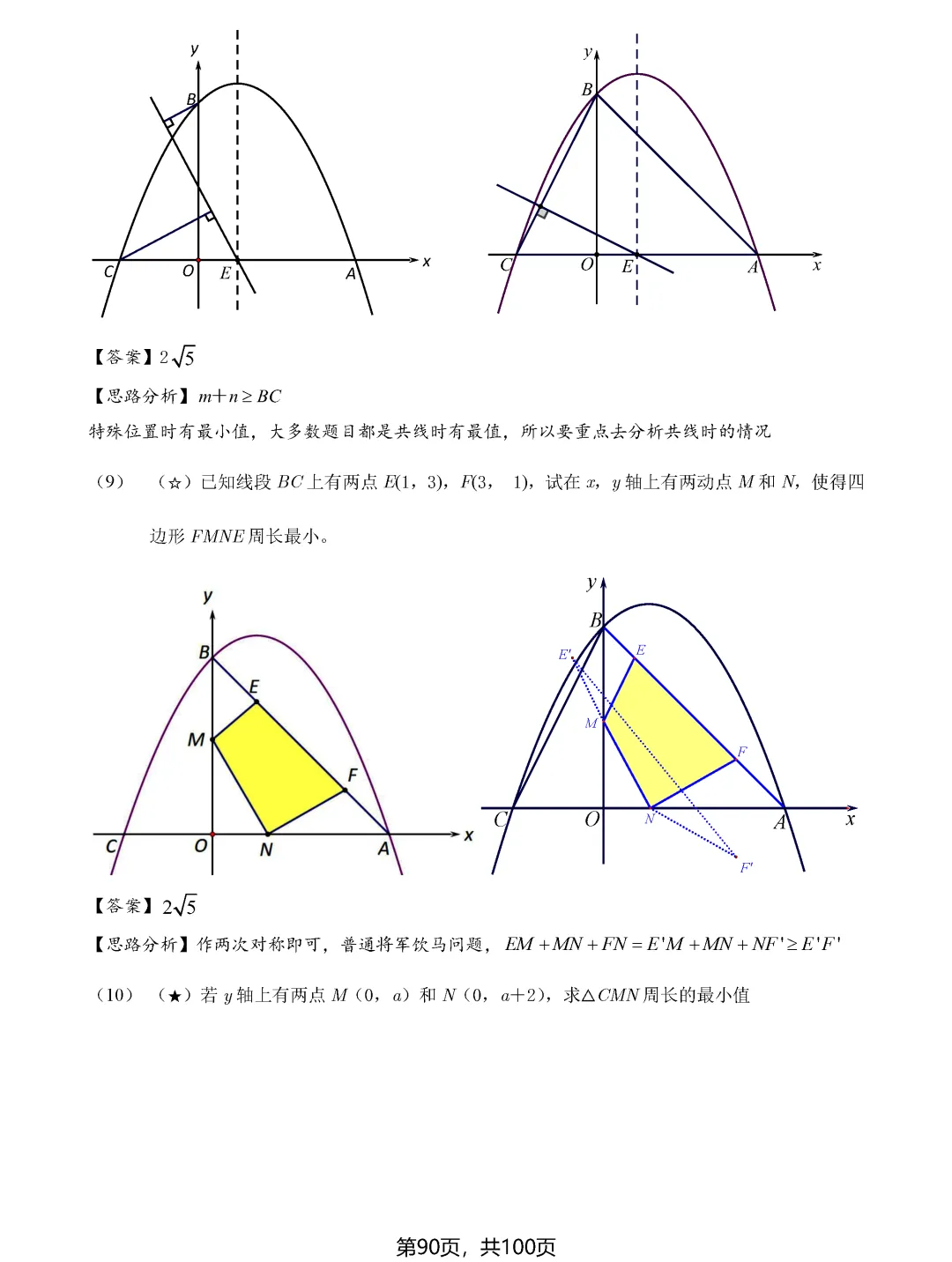
最值问题的根基在于"将军饮马"模型,这是初中几何最值问题的源头。其核心思想是利用对称性将折线转化为直线,依据"两点之间线段最短"这一基本公理求解。当遇到在直线上找一点使两线段之和最小的问题时,只需作其中一个定点关于直线的对称点,连接对称点与另一个定点,与直线的交点即为所求位置。这种方法不仅适用于单动点问题,通过两次对称还能解决双动点问题,比如求三角形周长最小值或四边形周长最小值的情况。
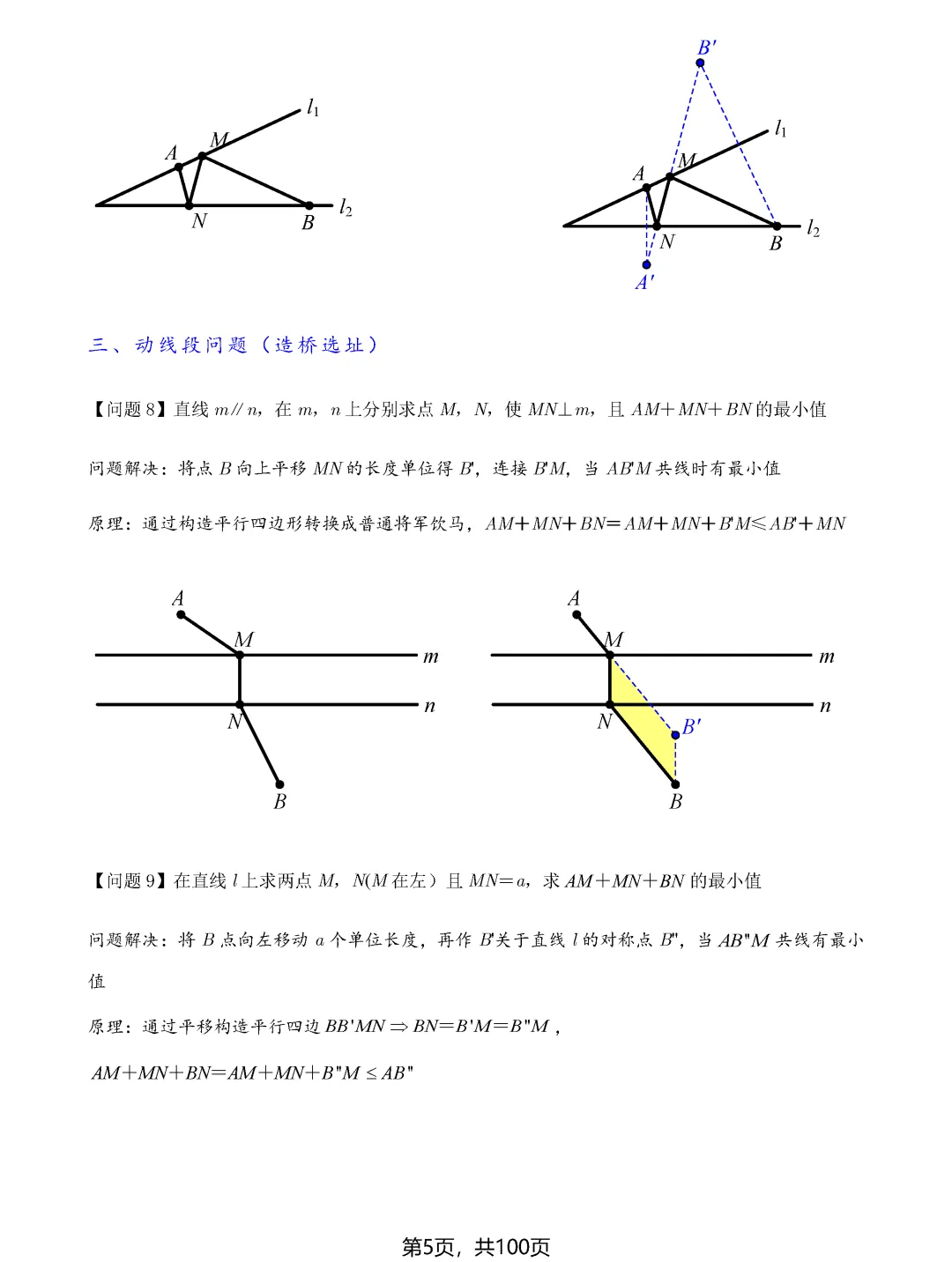
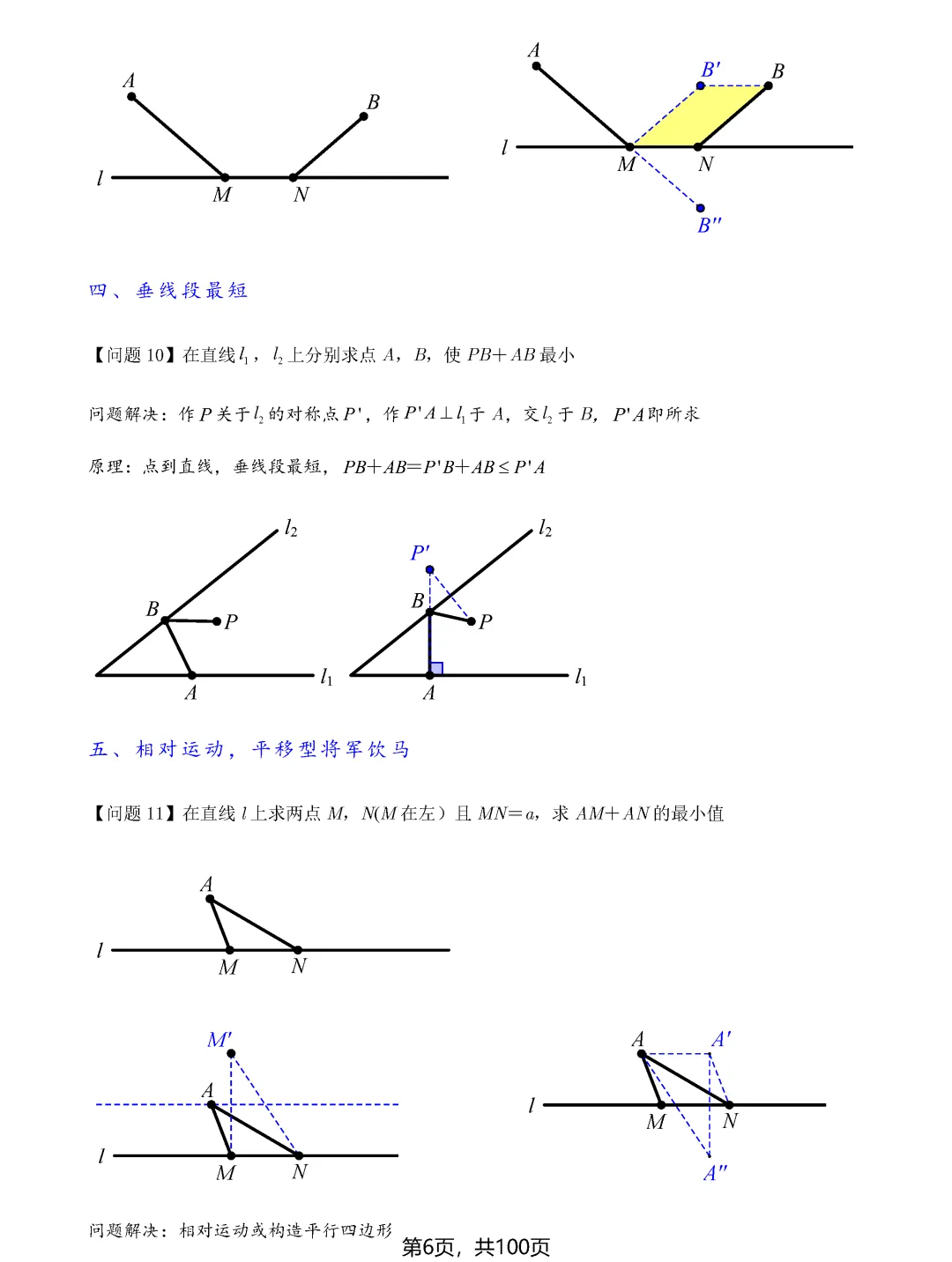
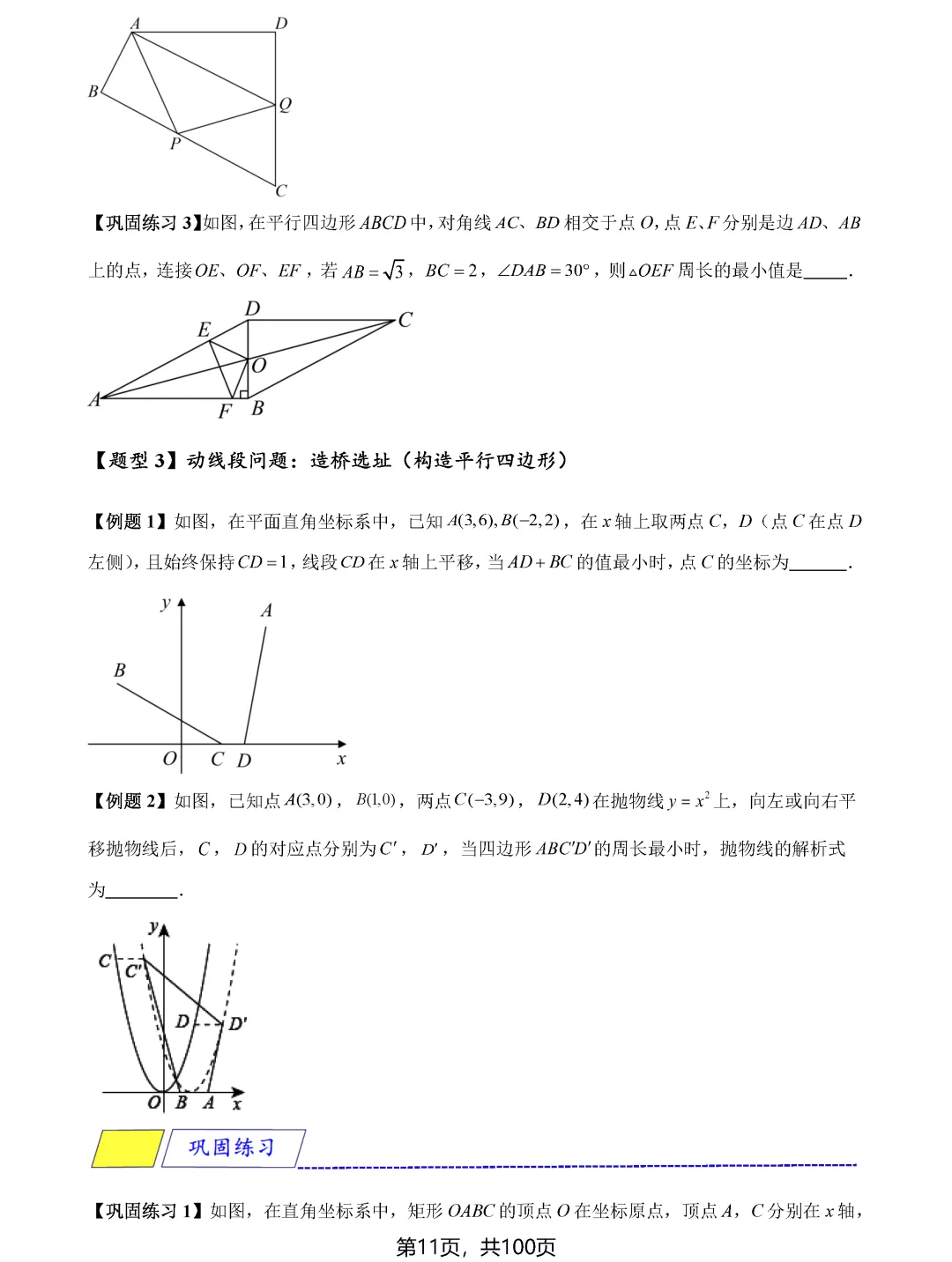
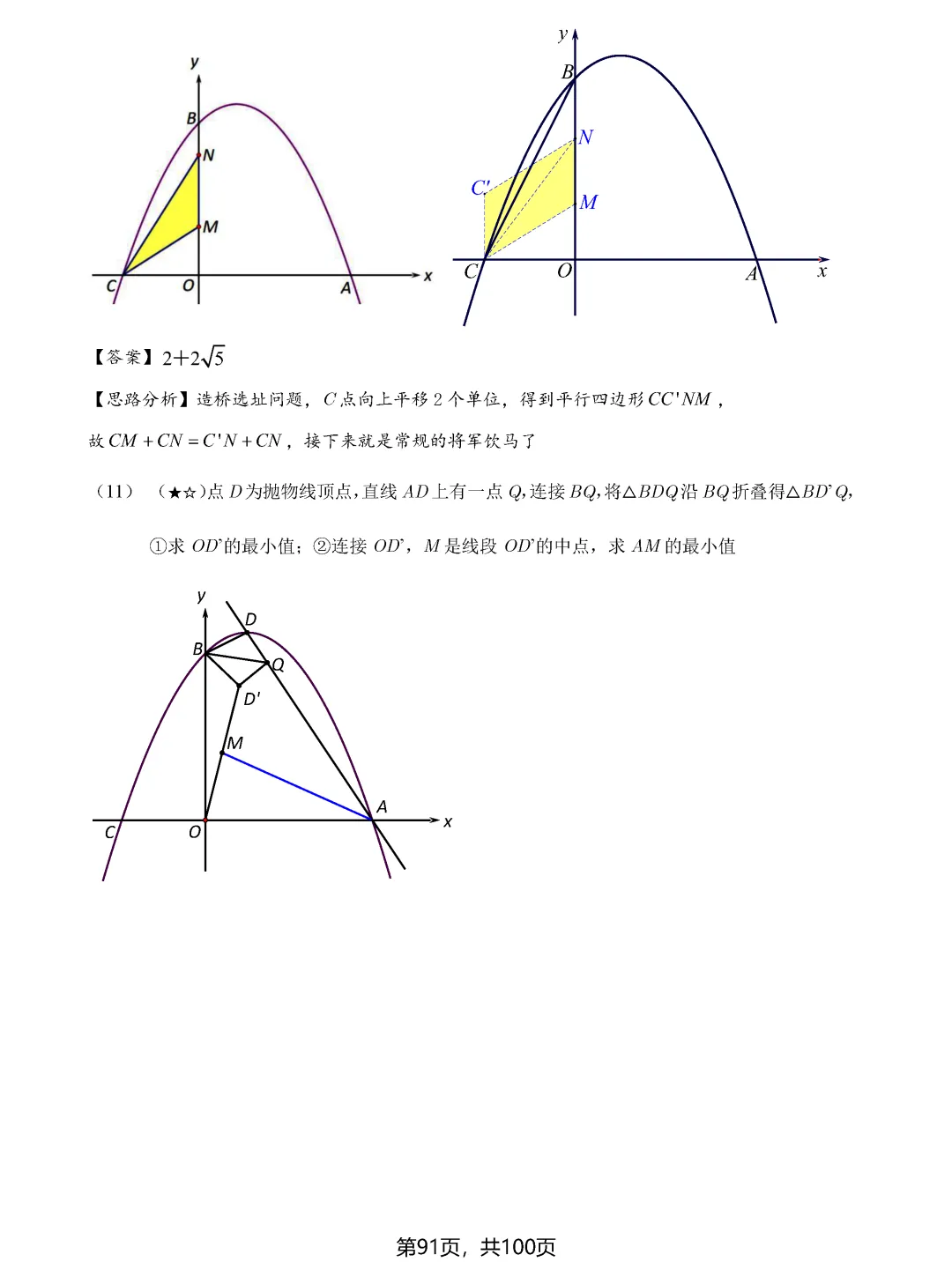
造桥选址问题是将军饮马模型的进阶应用。当需要在两条平行线之间架一座垂直于平行线的桥,使从一点到另一点的路径最短时,可以通过平移变换,将问题转化为普通的将军饮马问题。具体做法是将其中一点向上或向下平移桥长的距离,再作对称点连线即可。这种化归思想是解决复杂最值问题的金钥匙。
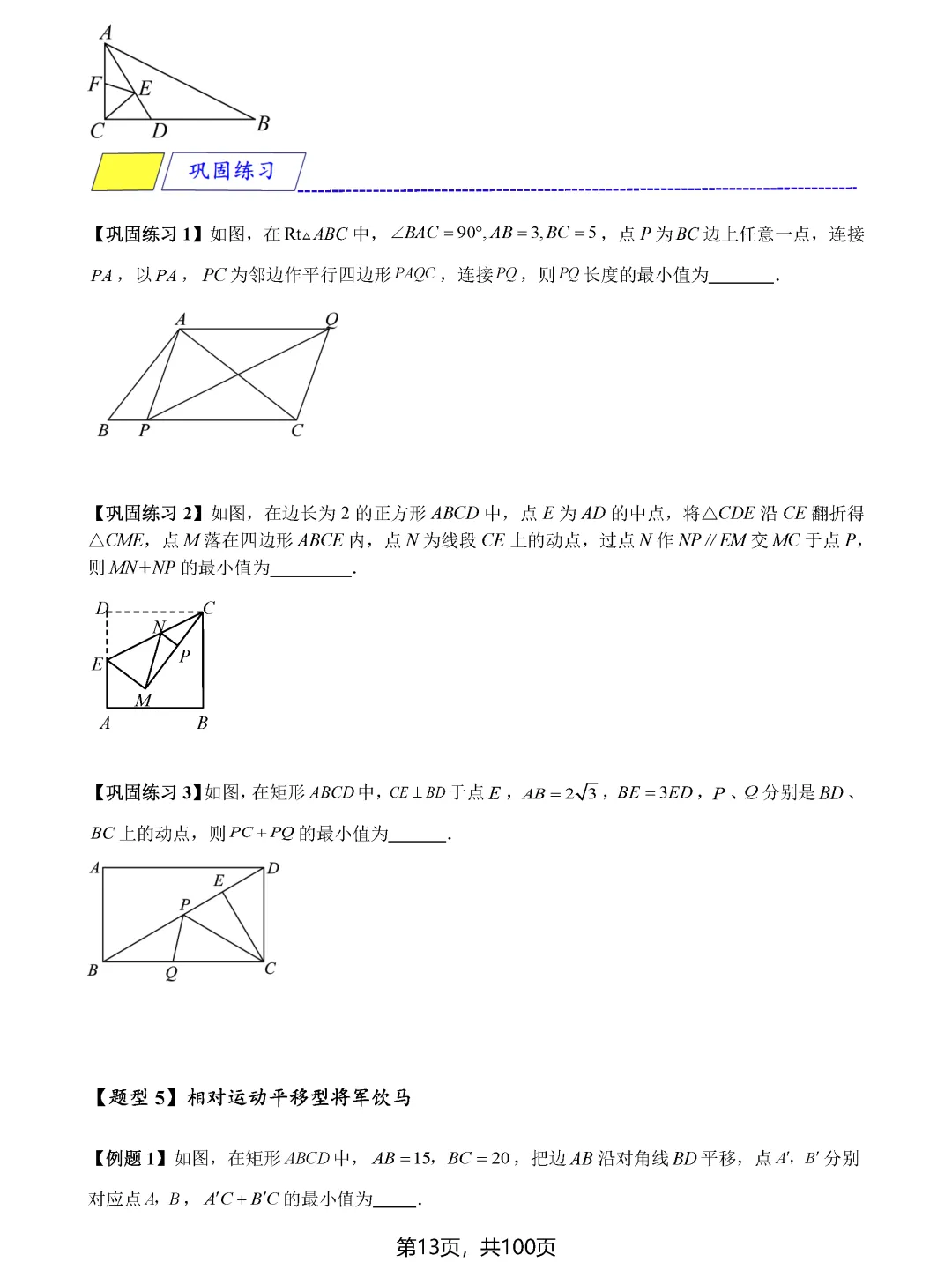
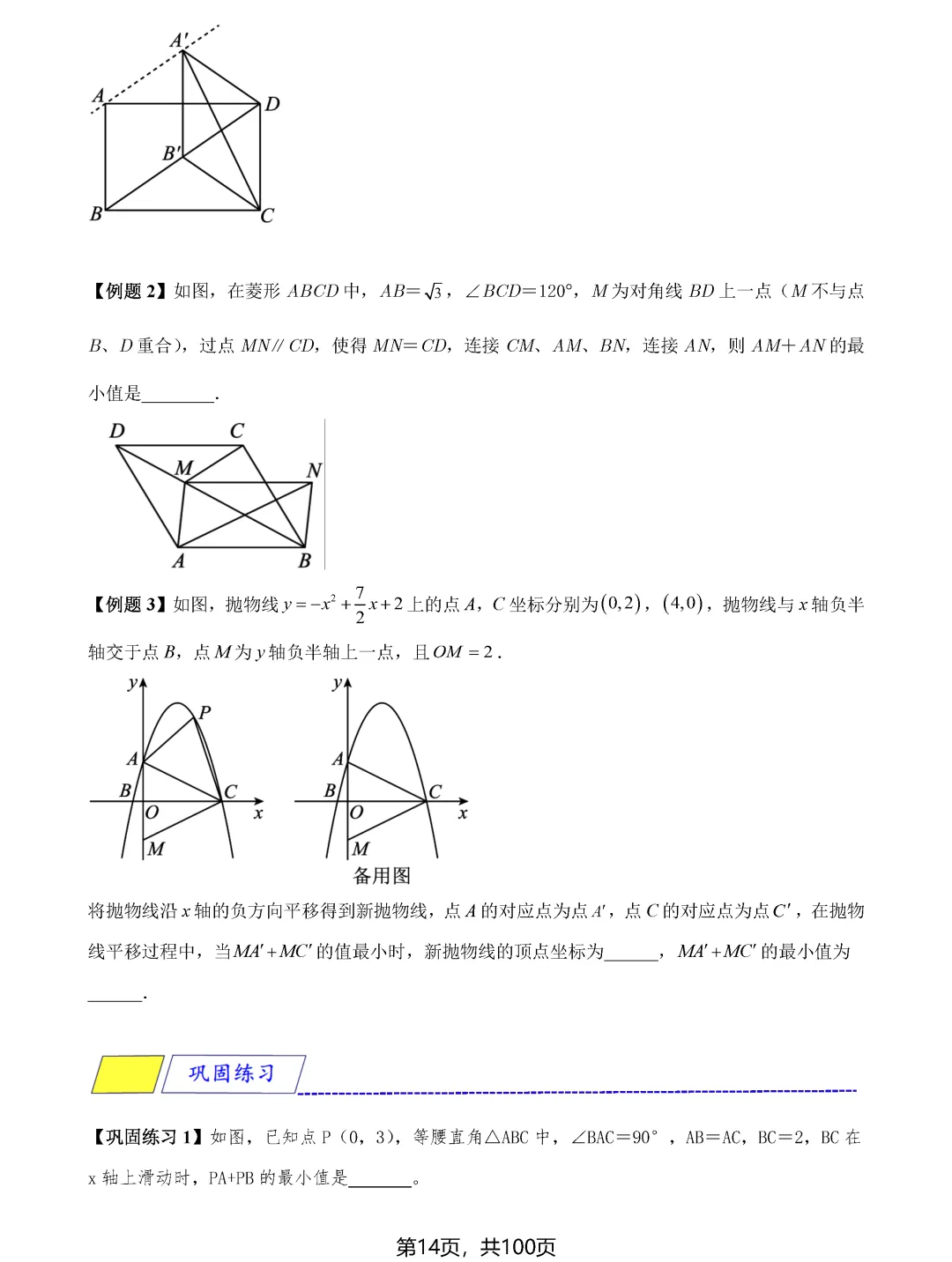
垂线段最短是另一个重要的最值原理。当需要求点到直线的距离最值时,垂线段往往就是答案。在相对运动问题中,通过构造平行四边形或利用平移变换,可以将动态问题转化为静态问题,从而找到最值点。
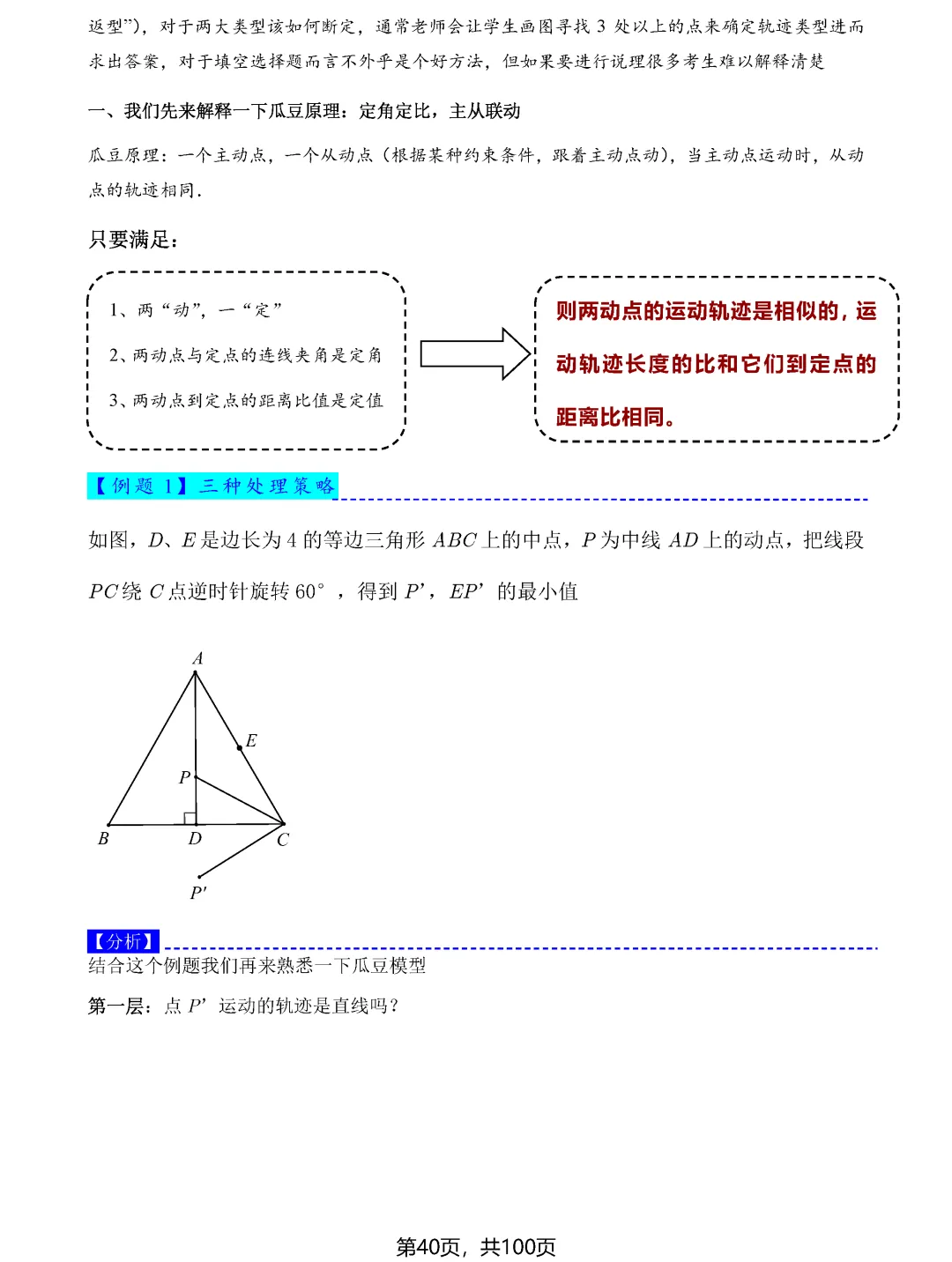
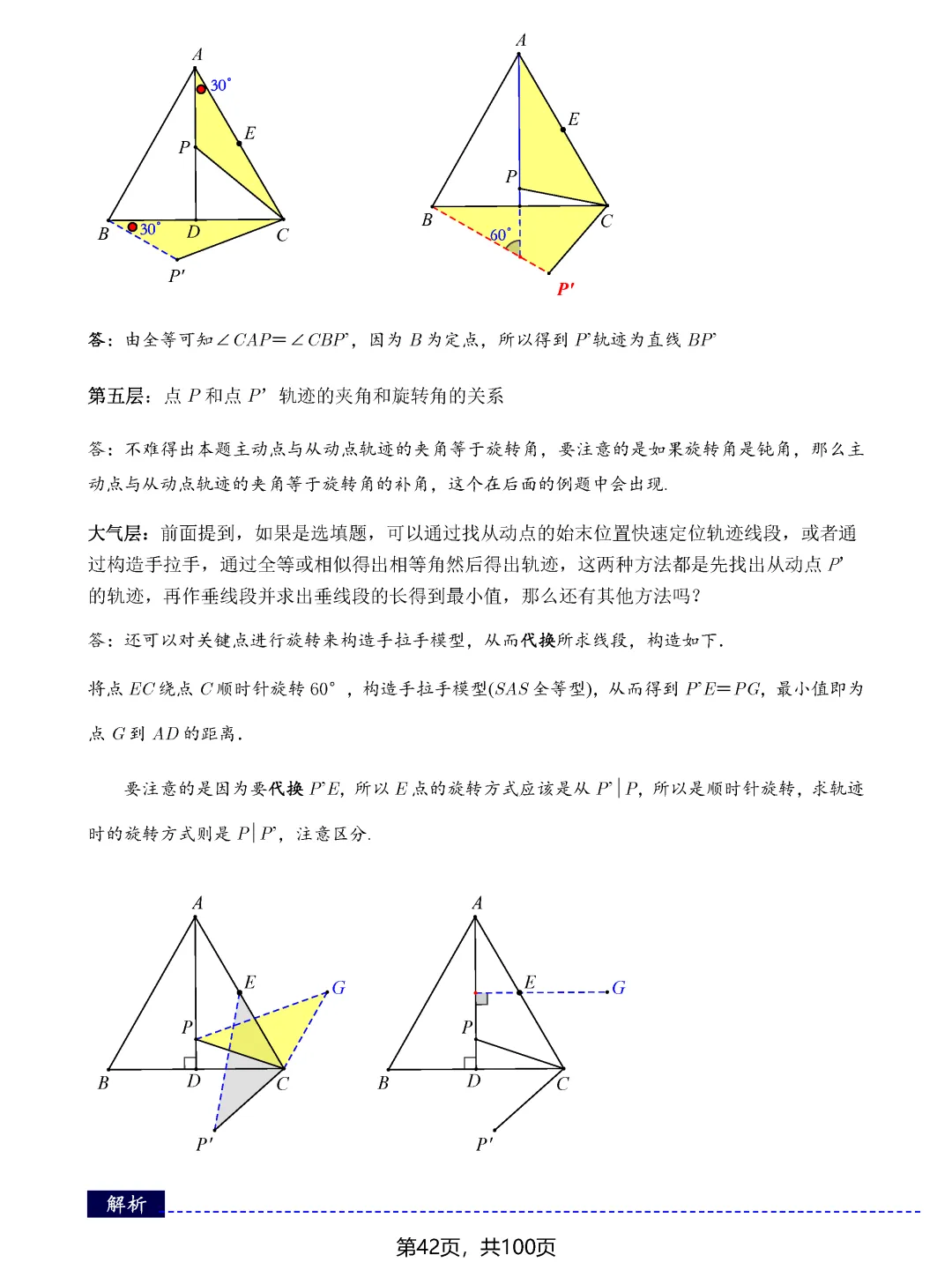
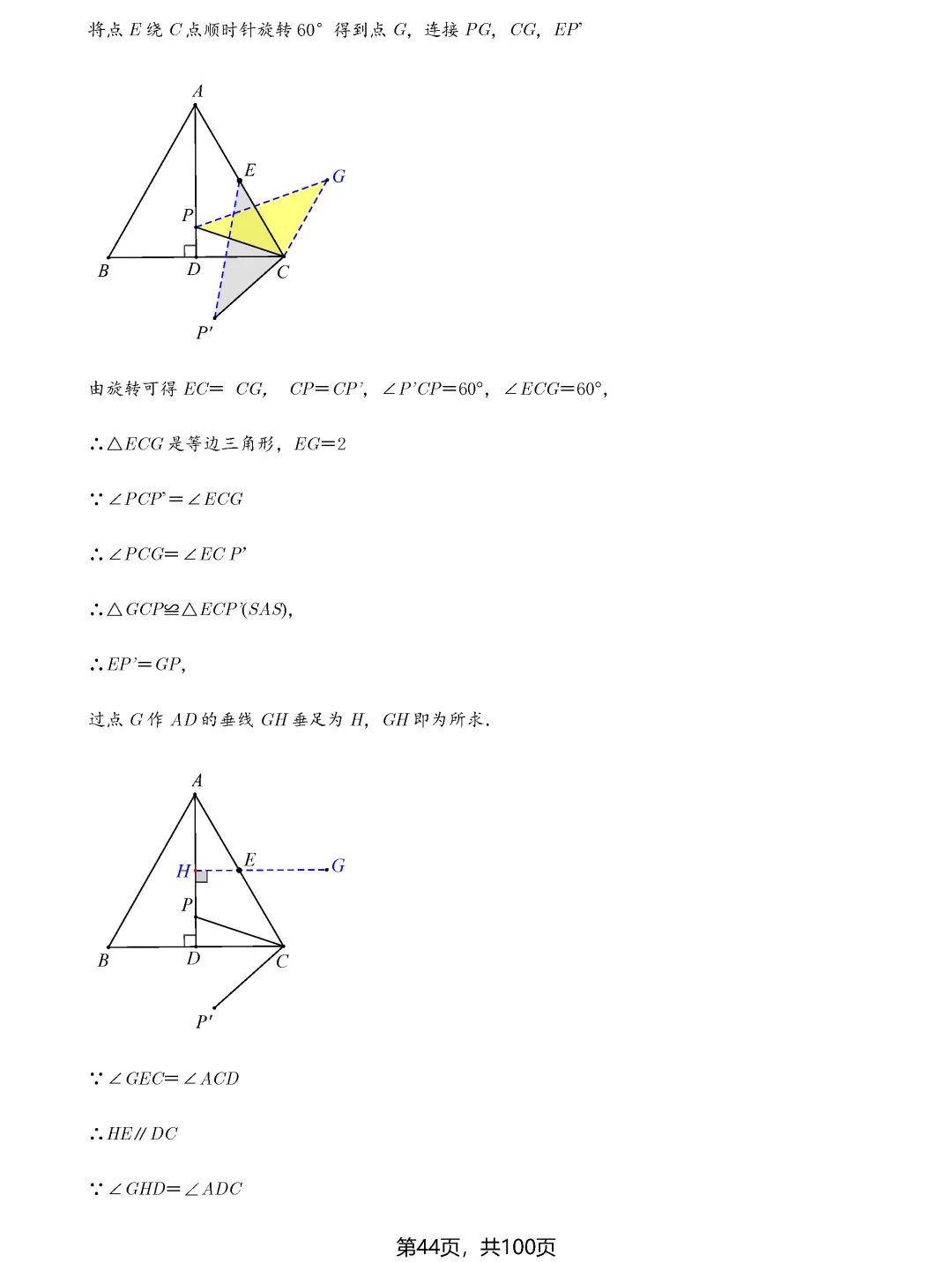
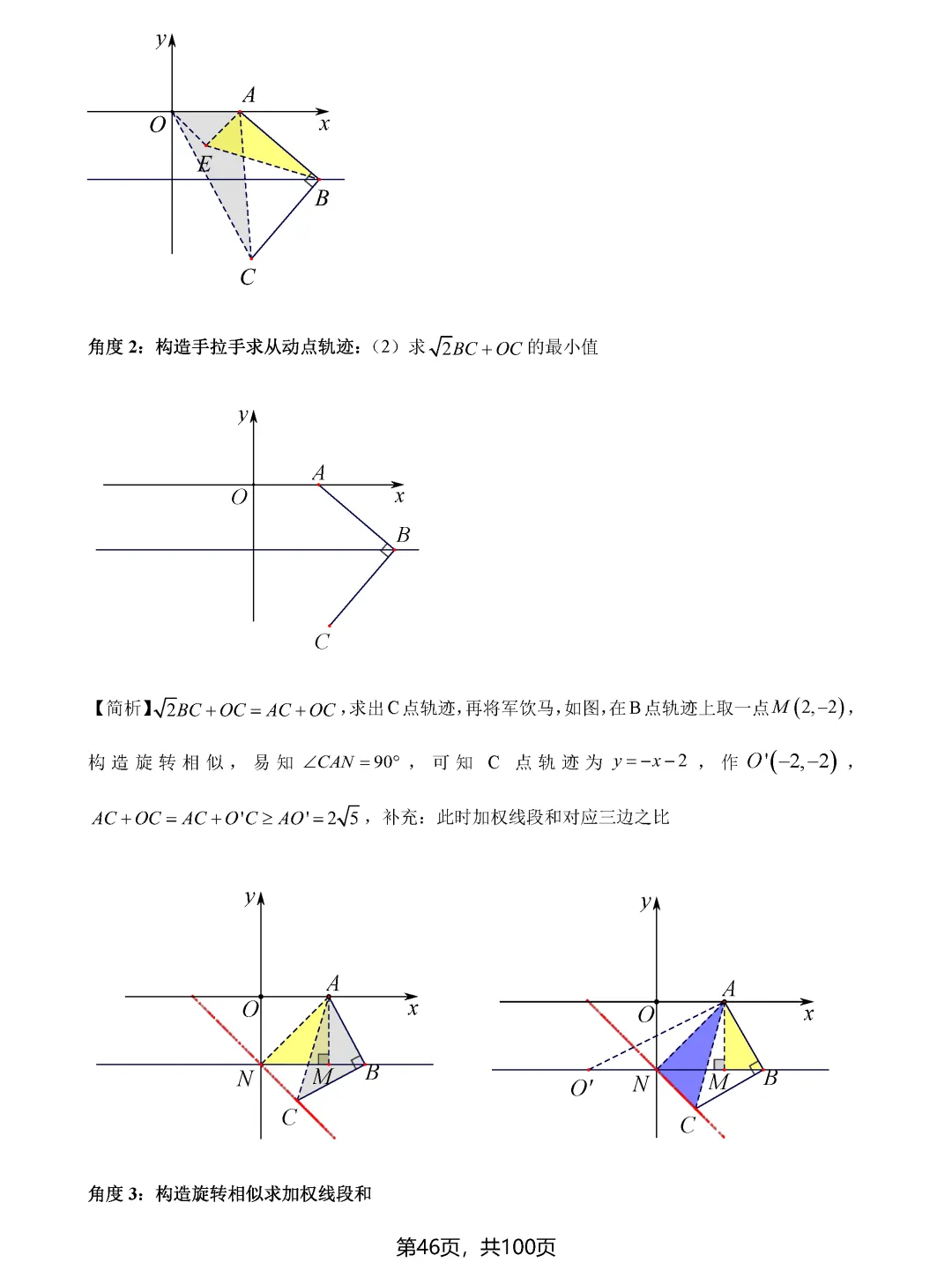
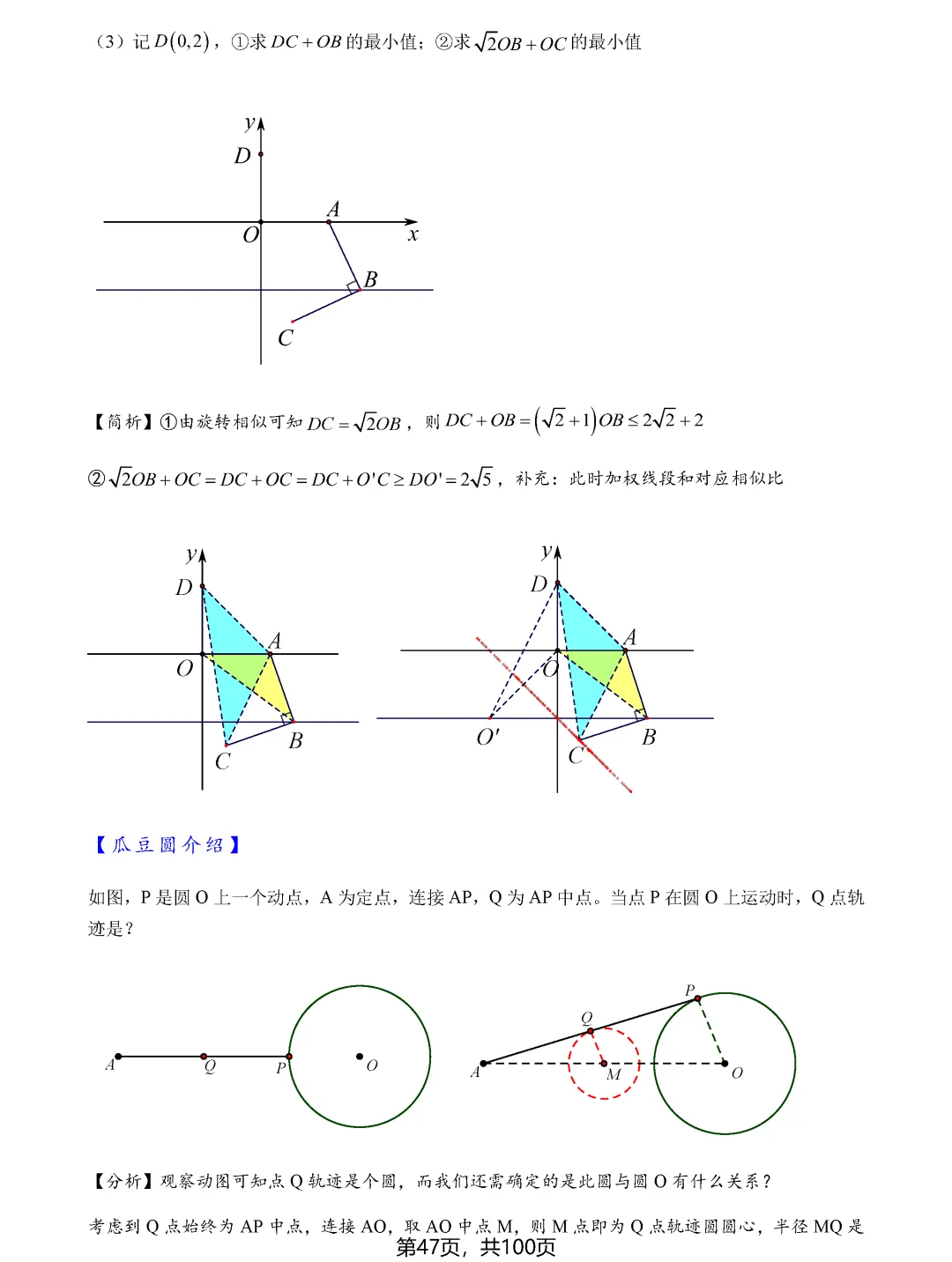
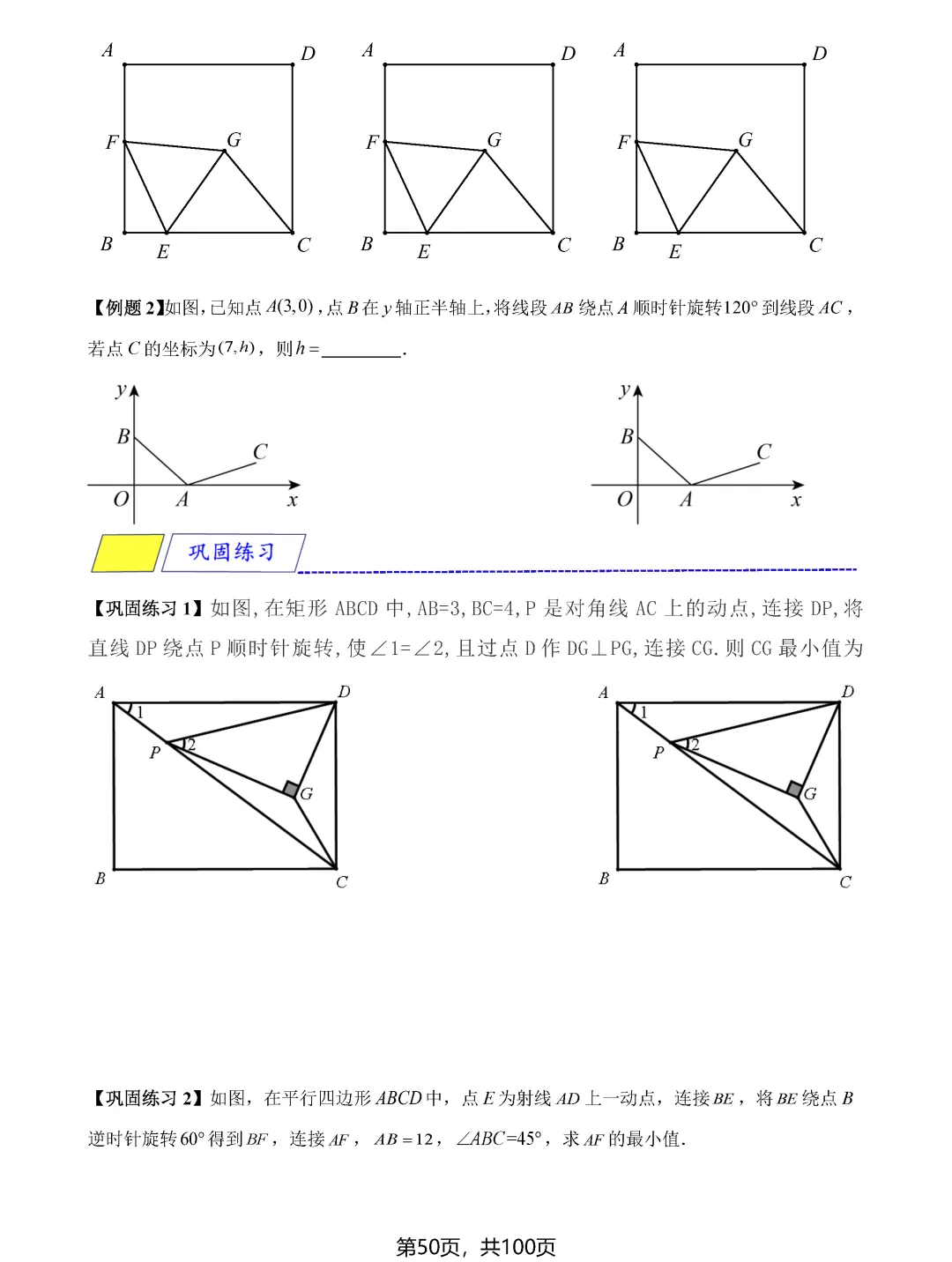
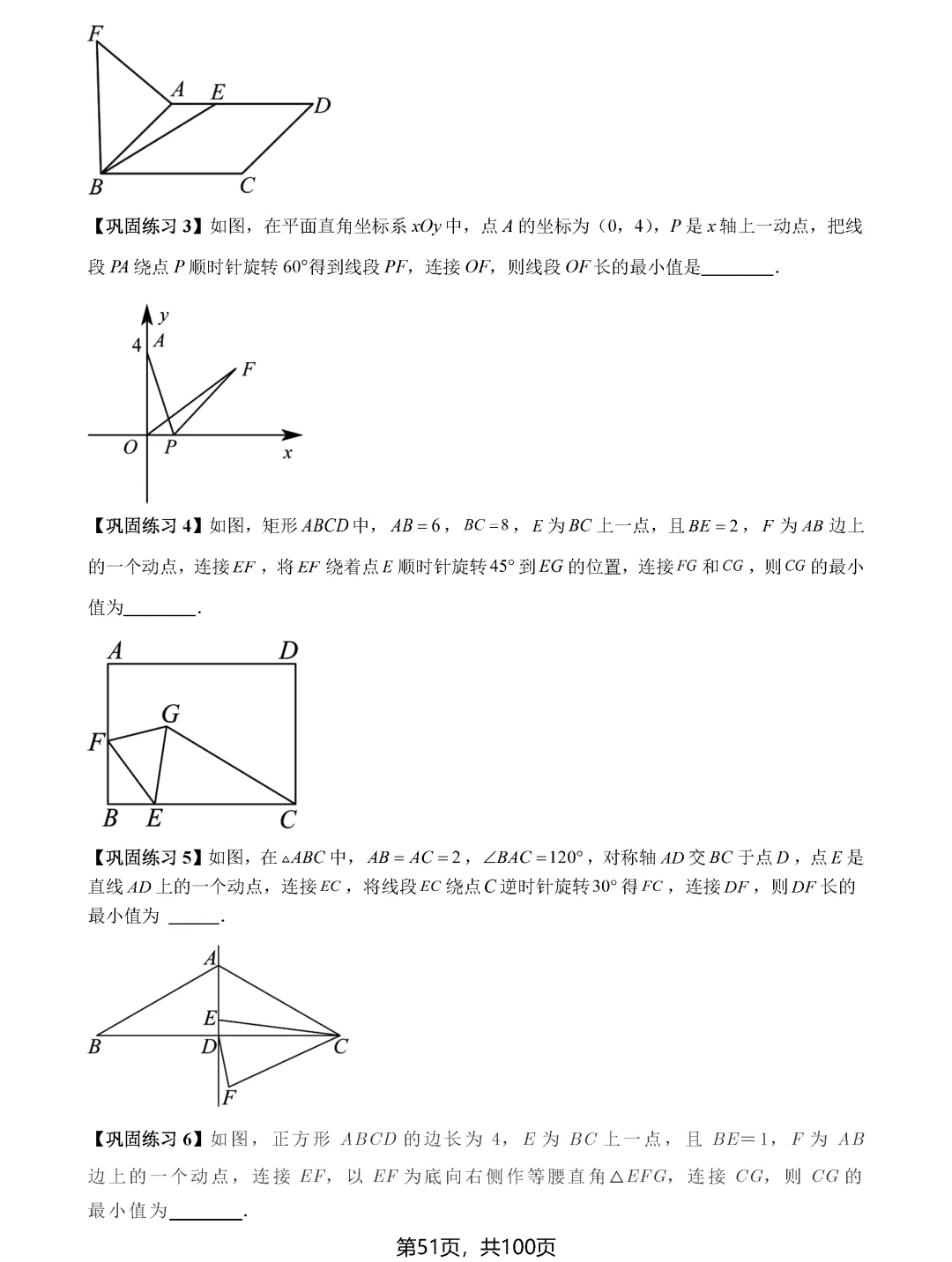
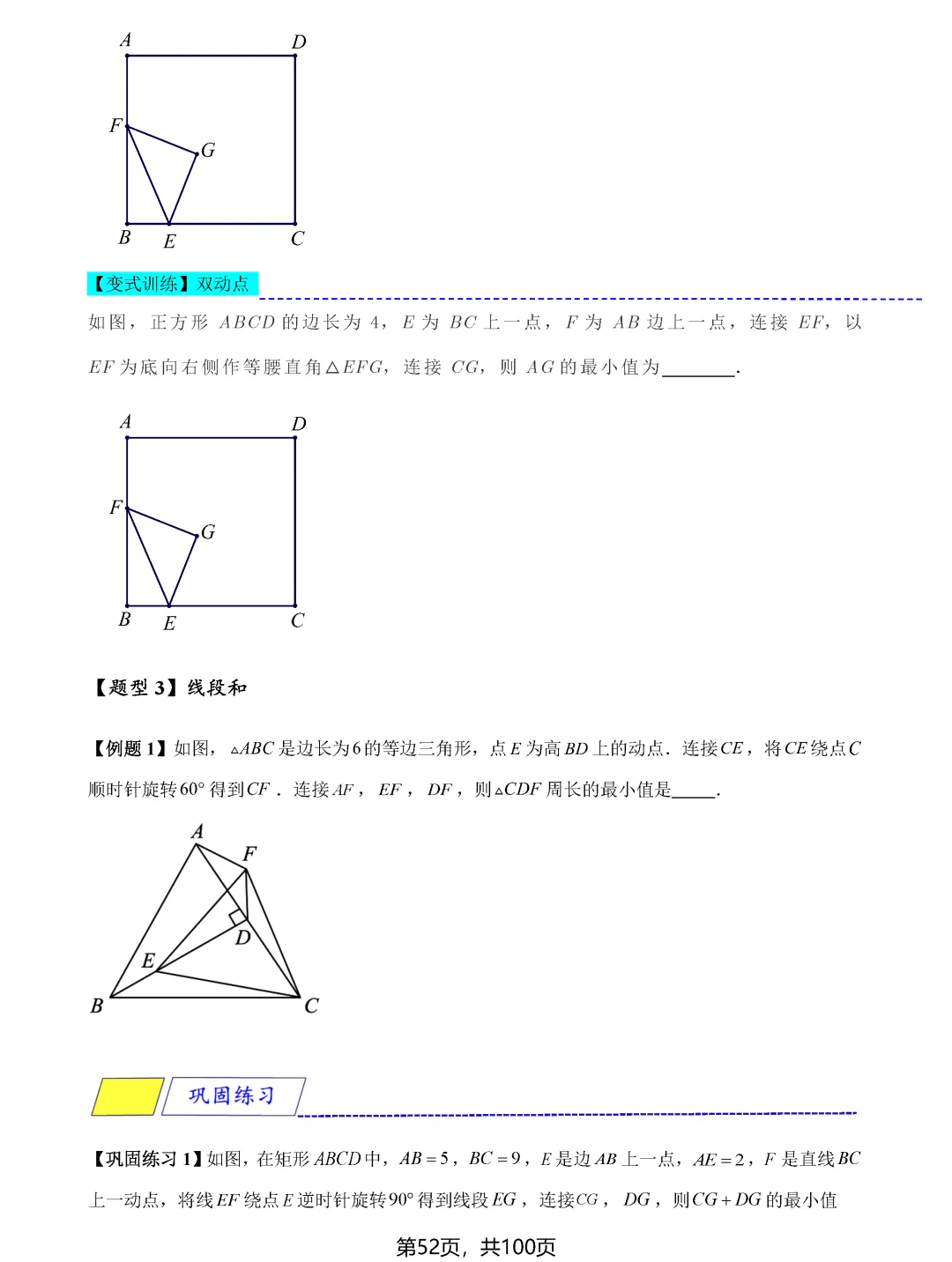
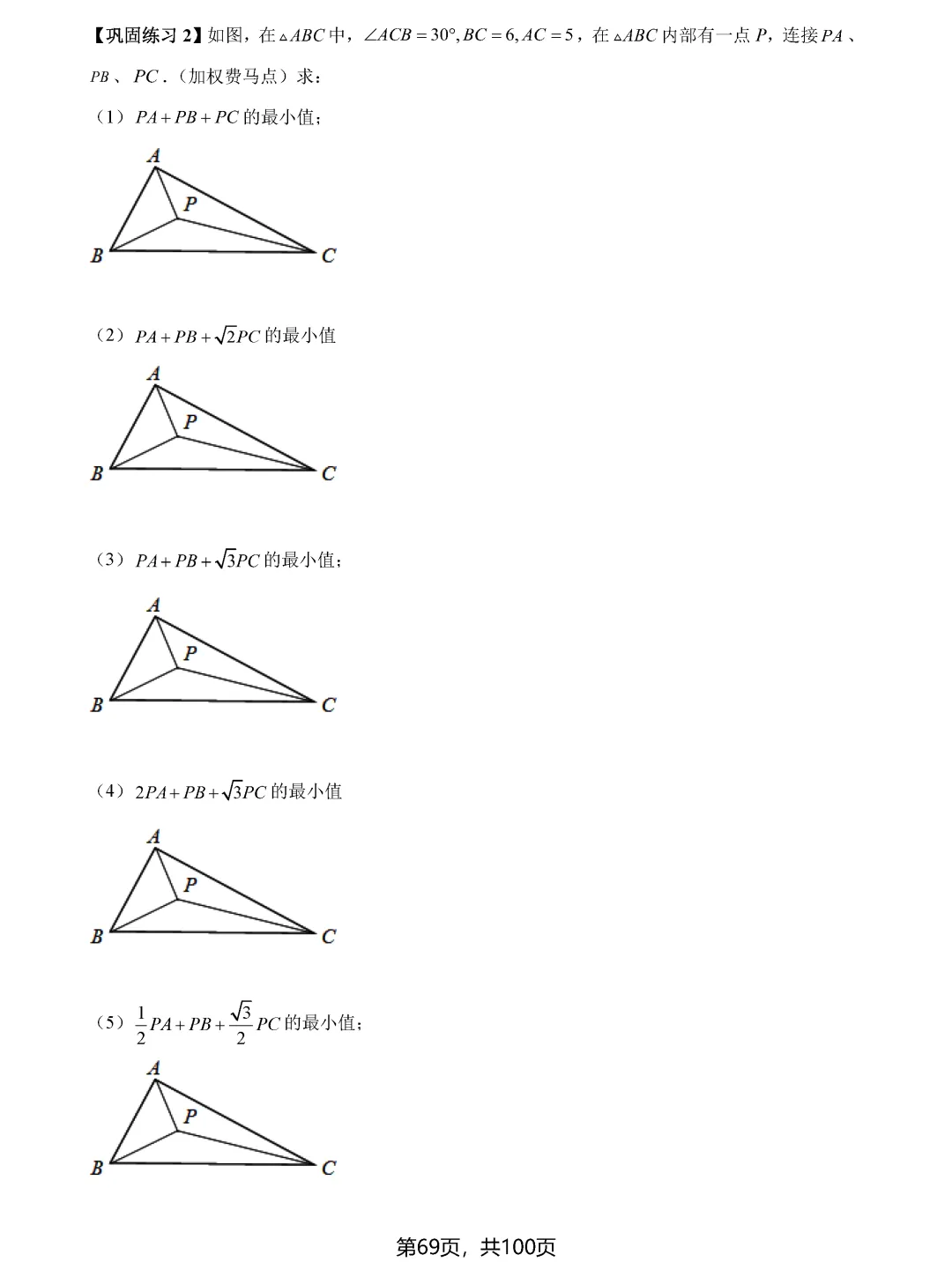
瓜豆原理和手拉手模型则揭示了轨迹与最值之间的深层联系。当一个点绕定点旋转或按固定比例缩放时,其轨迹往往形成圆或直线。确定轨迹后,再利用圆的性质或直线性质求最值就变得顺理成章。比如阿氏圆问题,通过构造相似三角形,可以将加权线段和转化为普通线段和,进而用圆外一点到圆上点的距离性质求解。
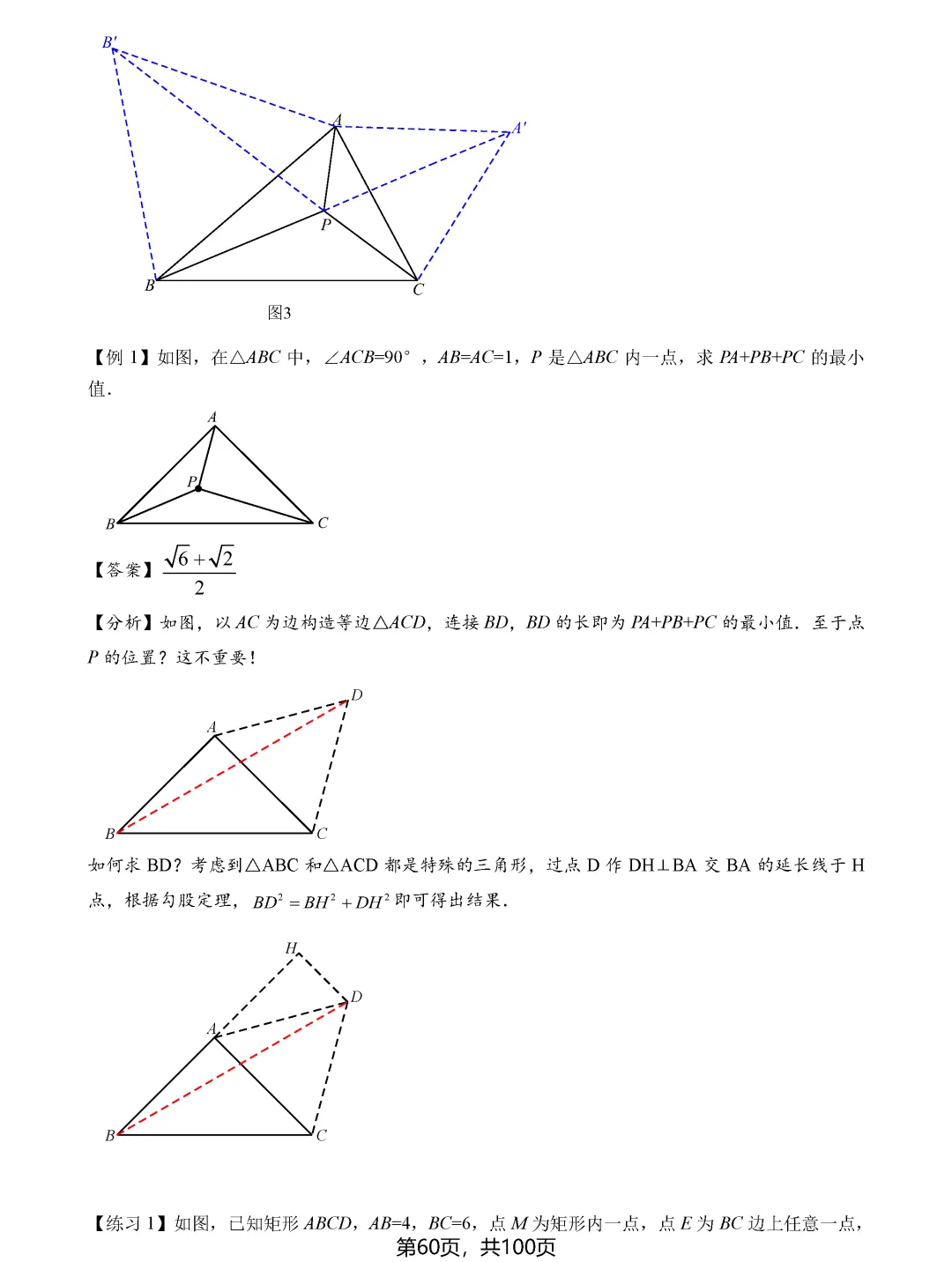
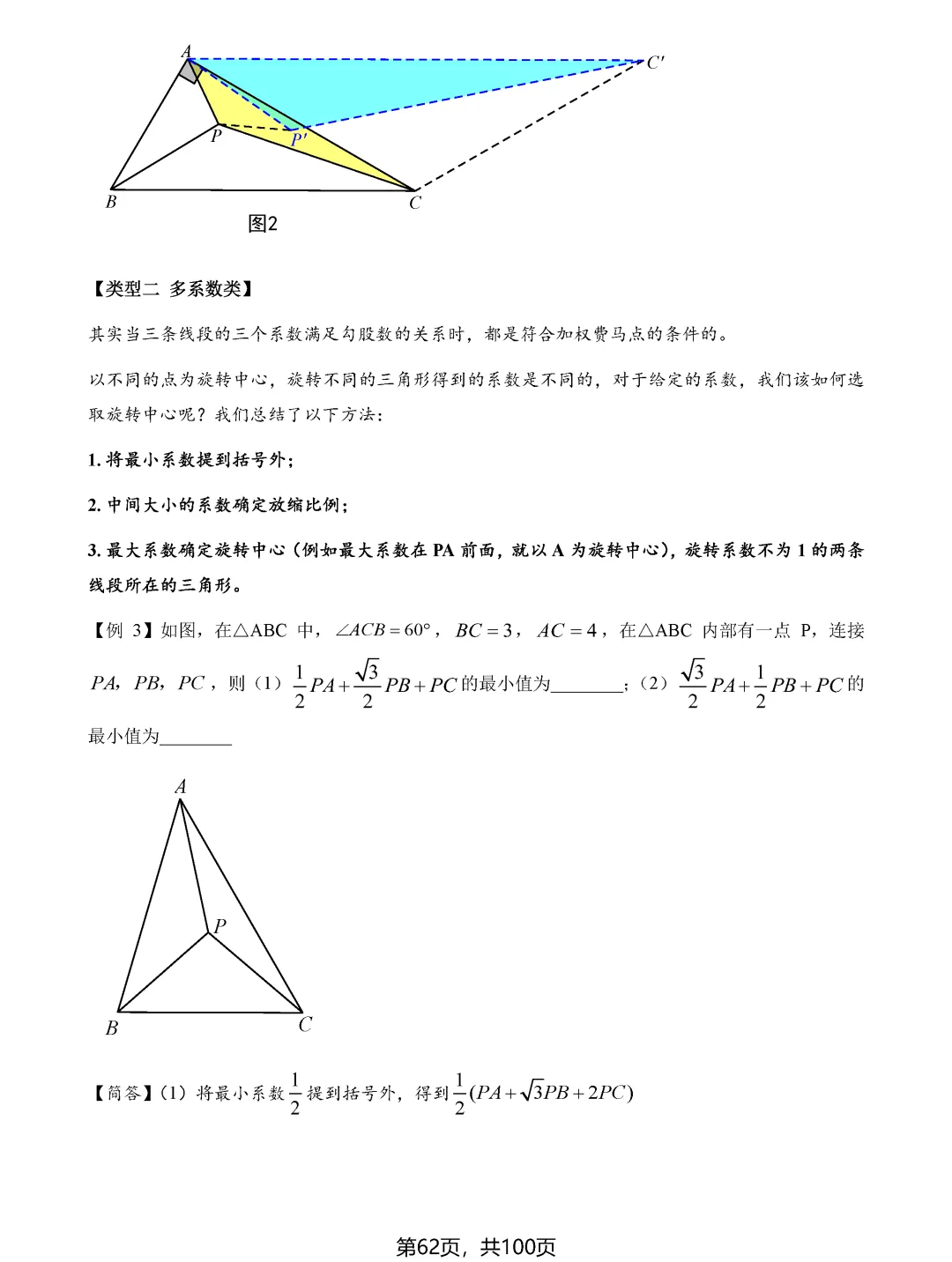
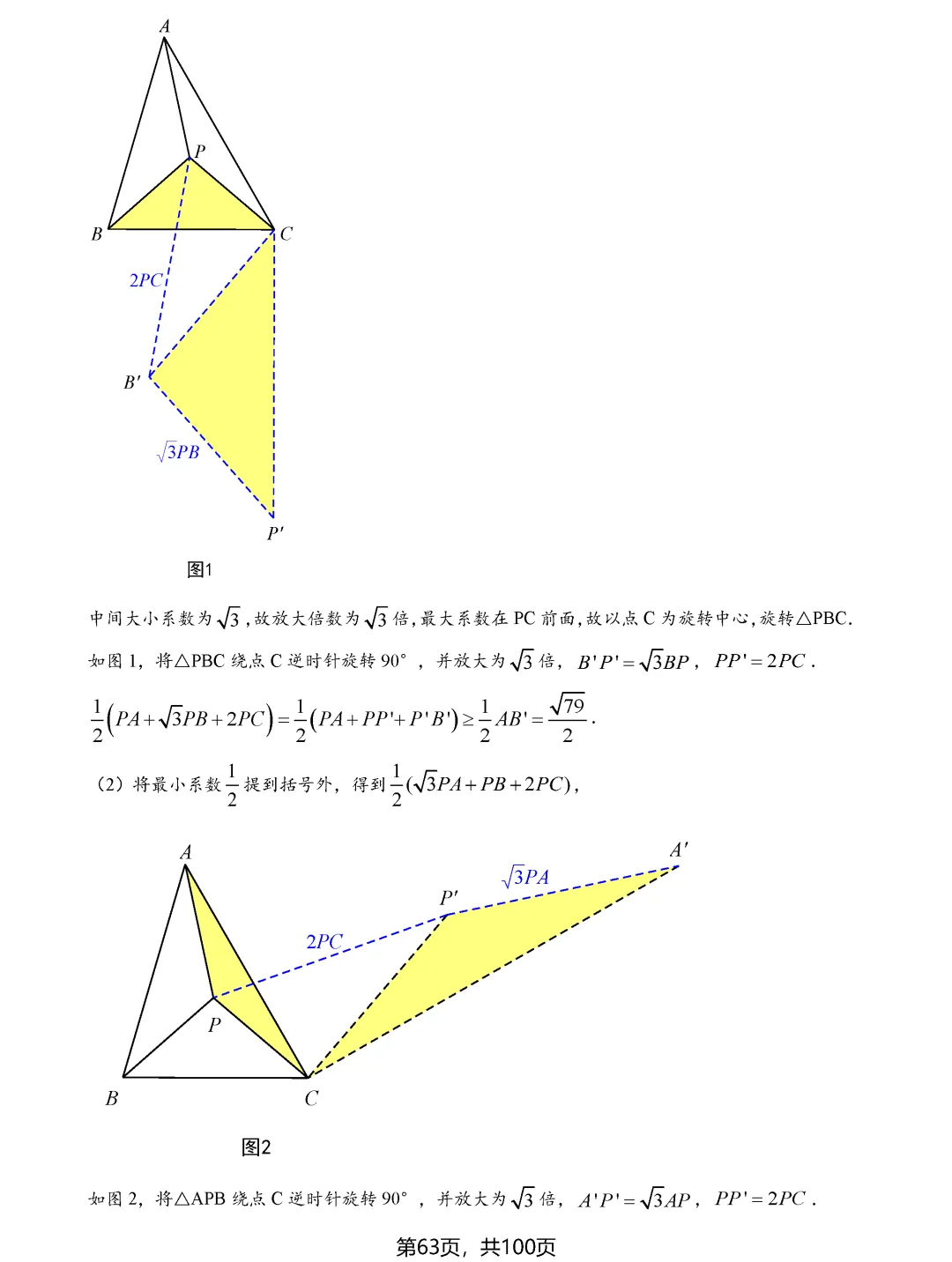
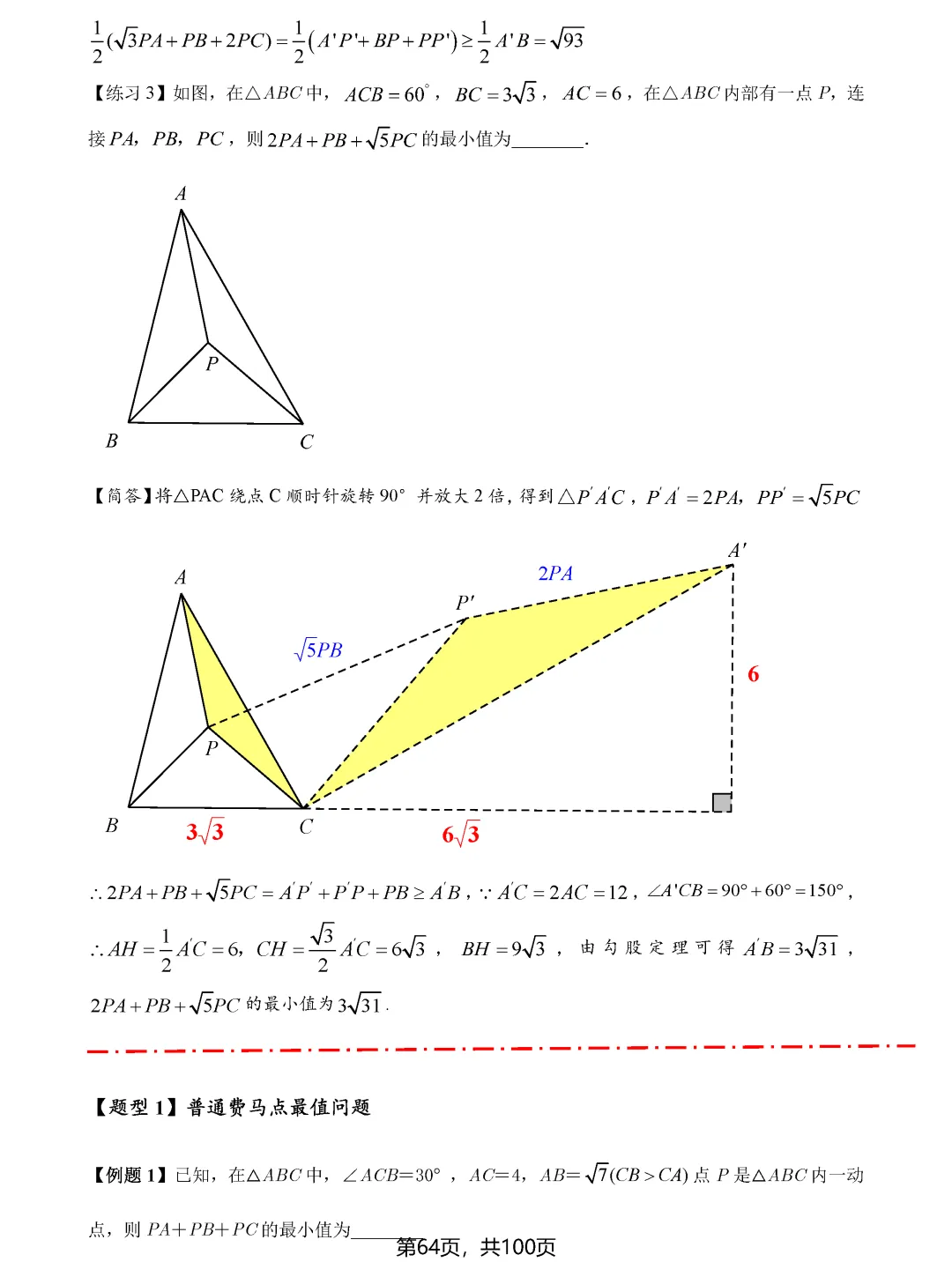
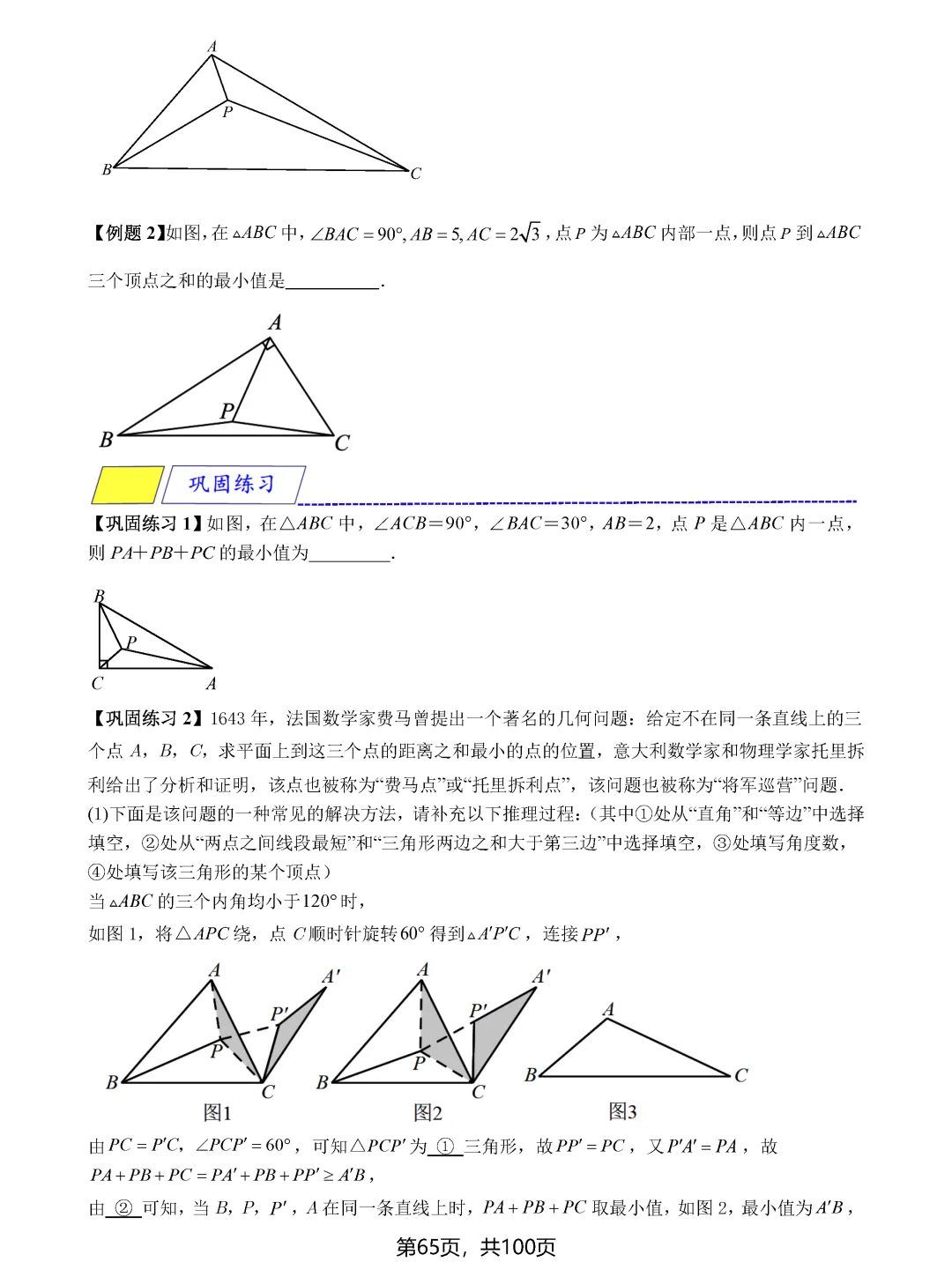
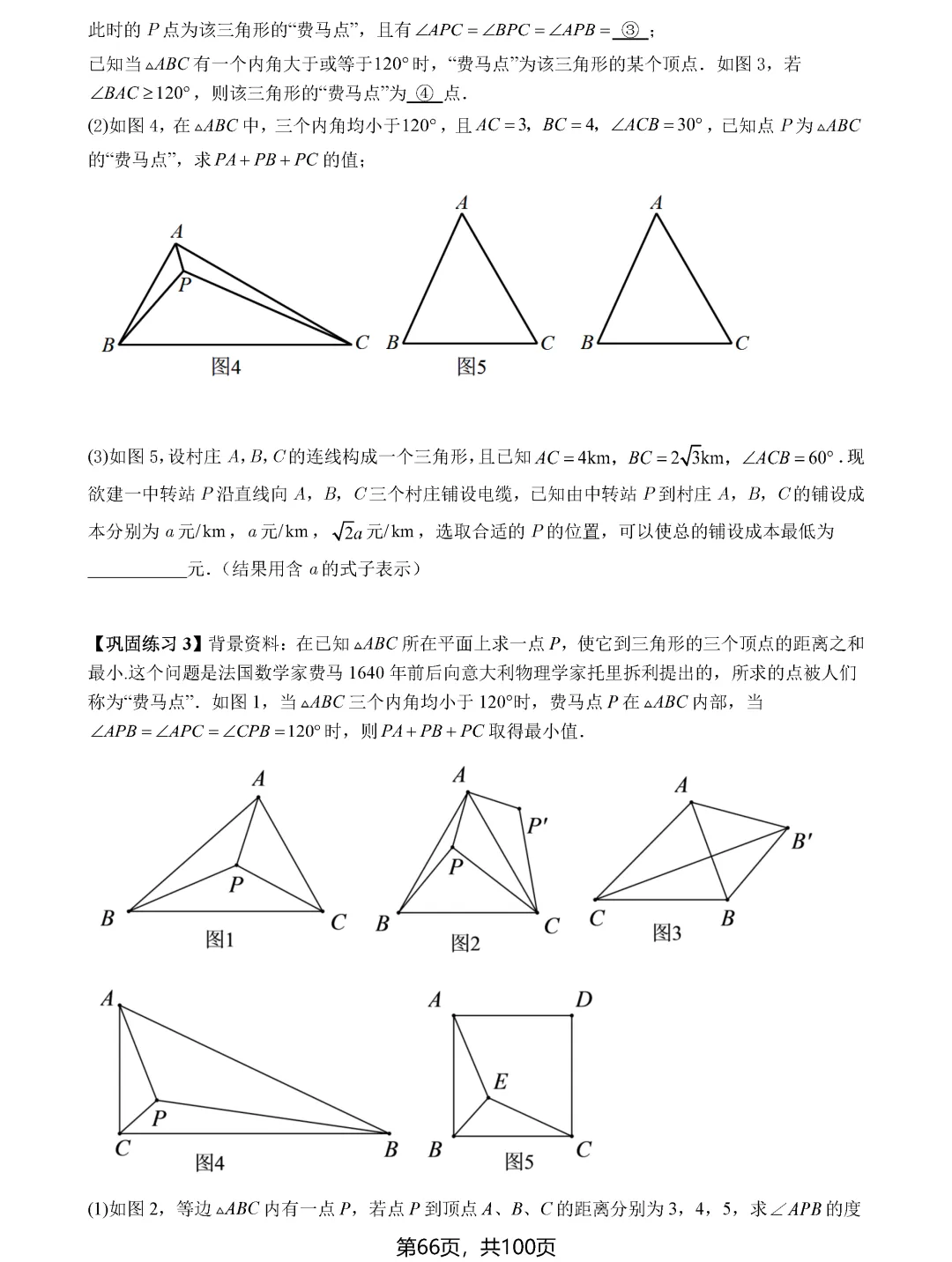
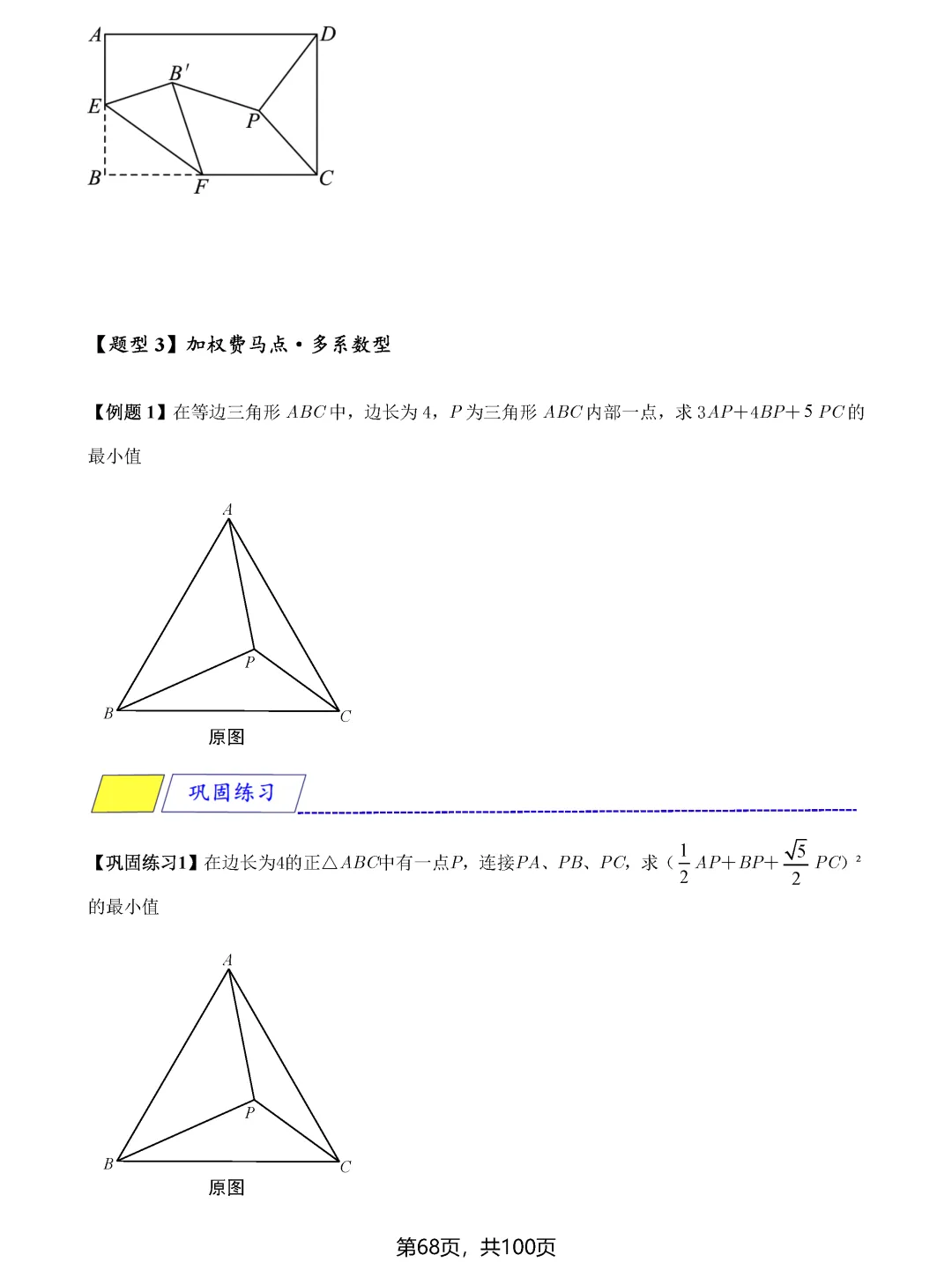
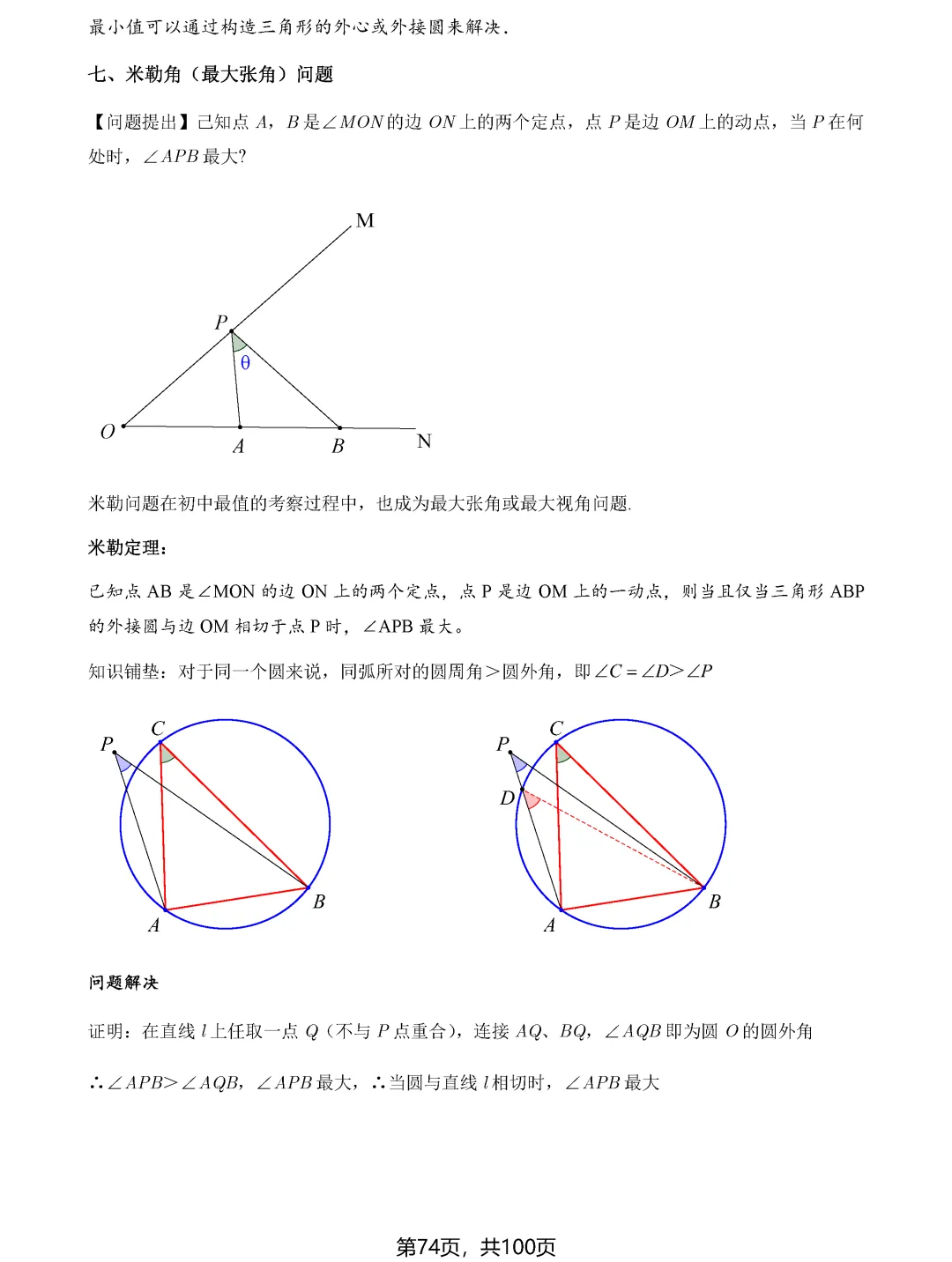
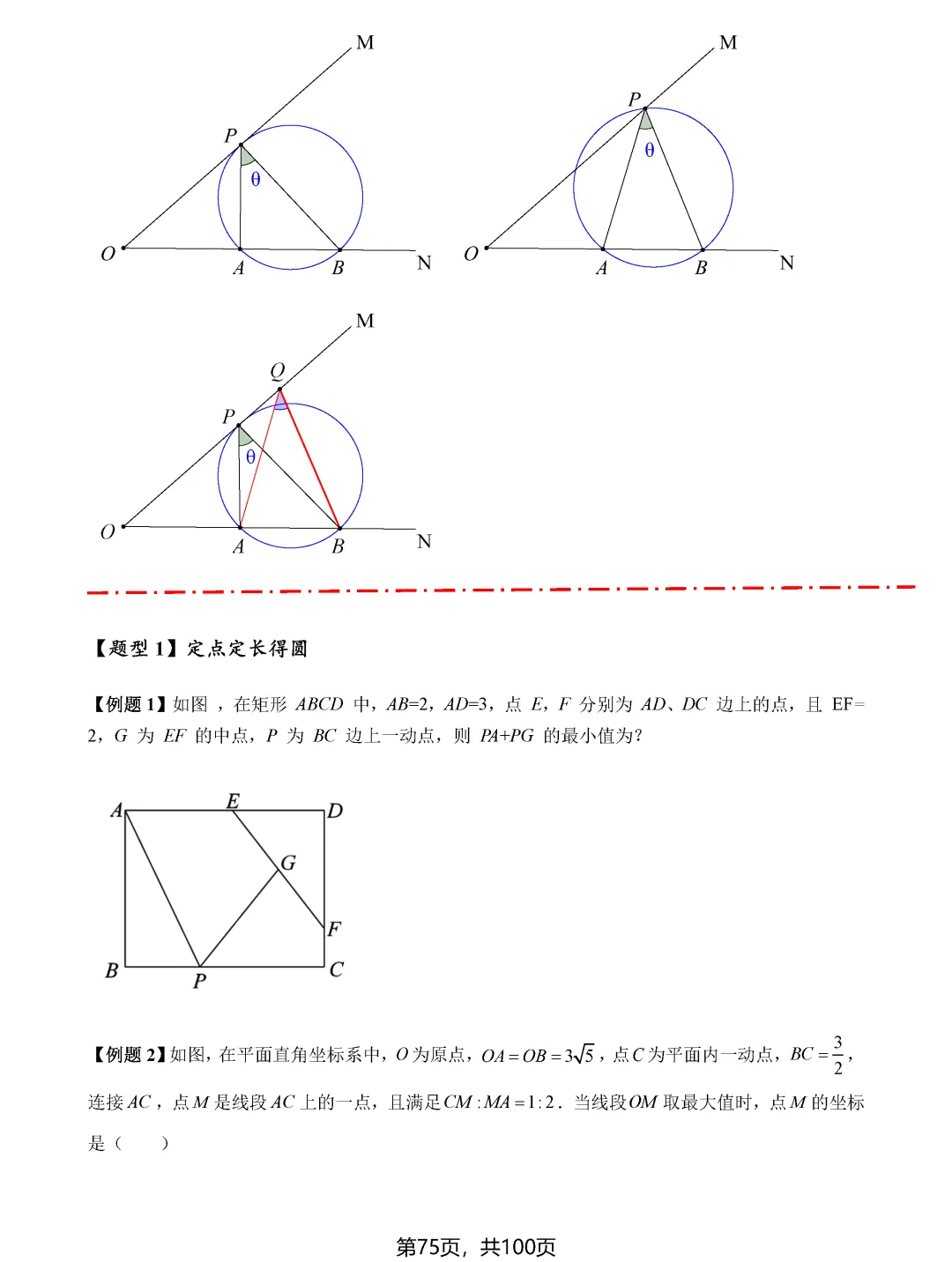
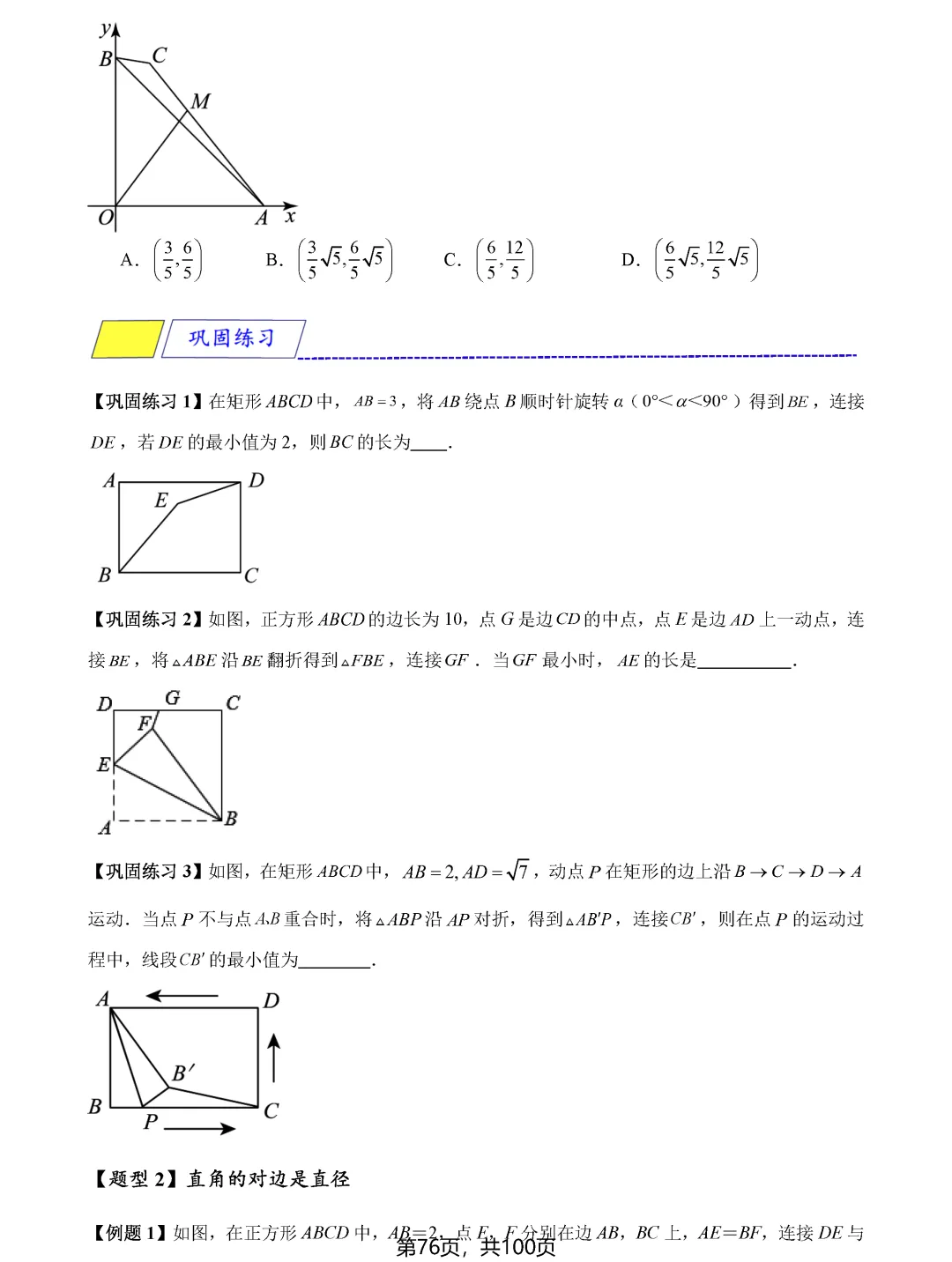
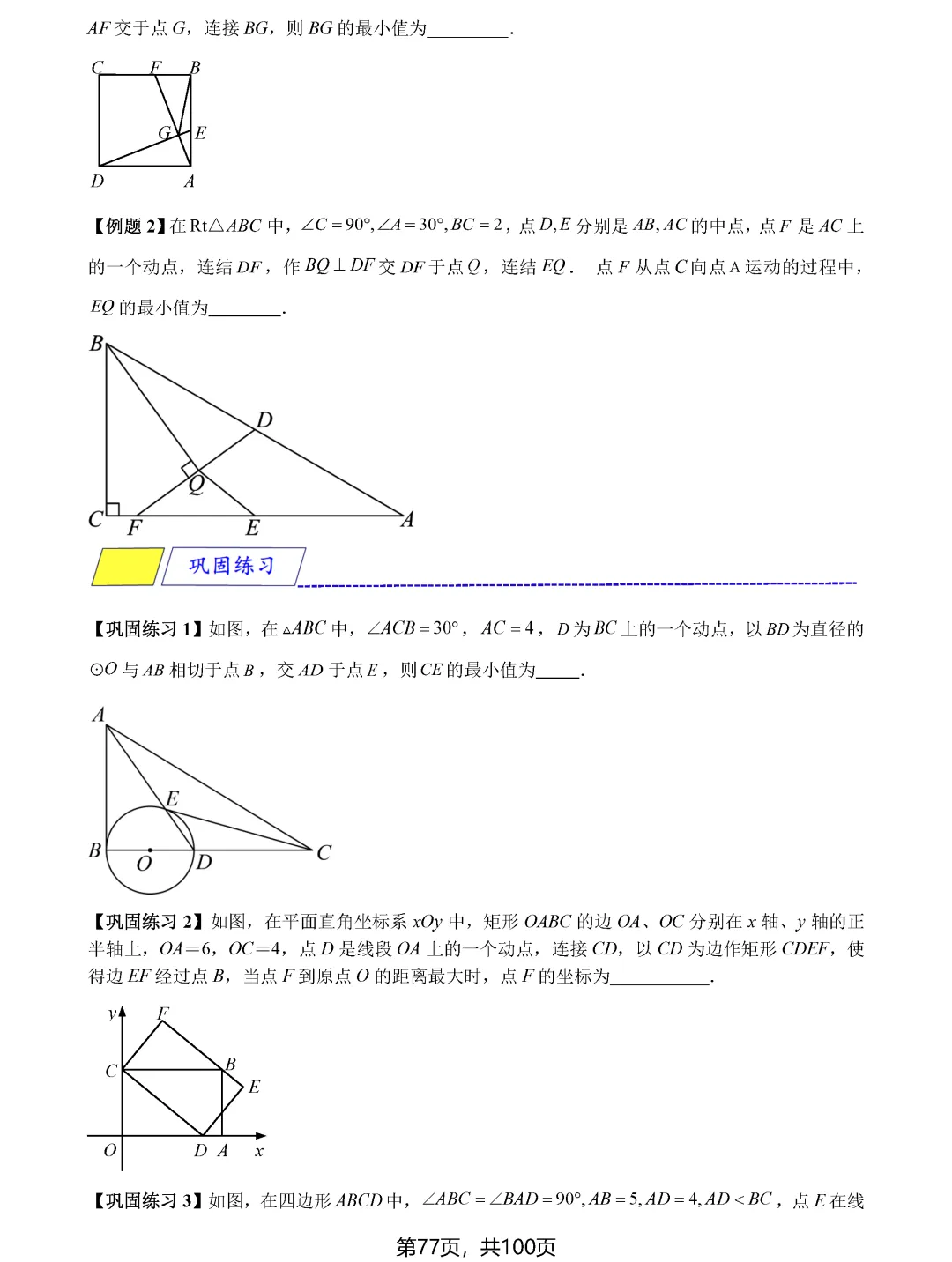
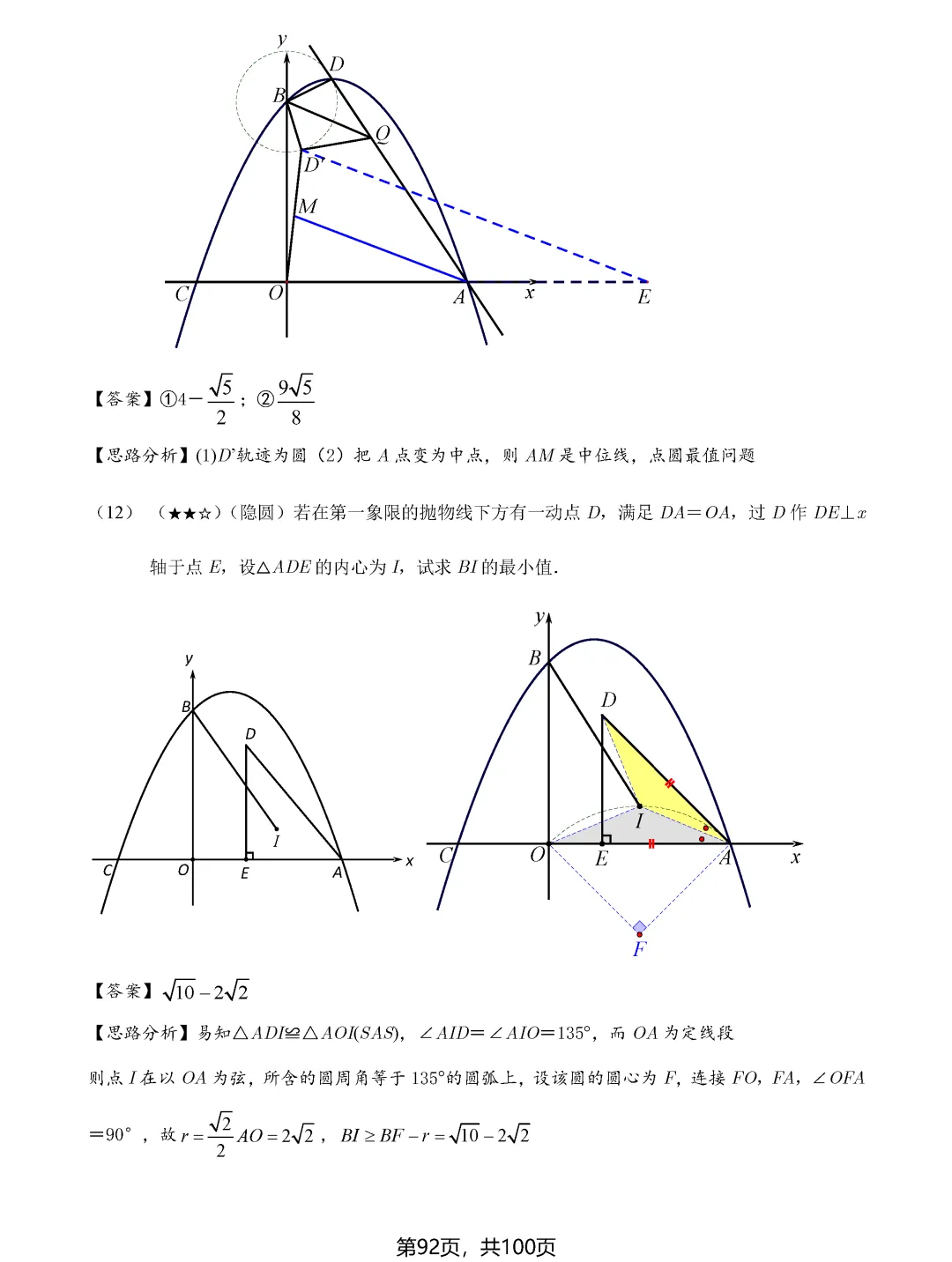
费马点问题考查的是到三角形三个顶点距离之和最小的点,当三角形各内角均小于120度时,费马点就是对各边张角均为120度的点;若有一个角大于等于120度,则该角的顶点即为费马点。隐圆最值问题则需要同学们具备敏锐的观察力,能够识别出定点定长、定弦定角等隐含的圆的条件,将问题转化为圆上动点到定点或定直线的距离问题。
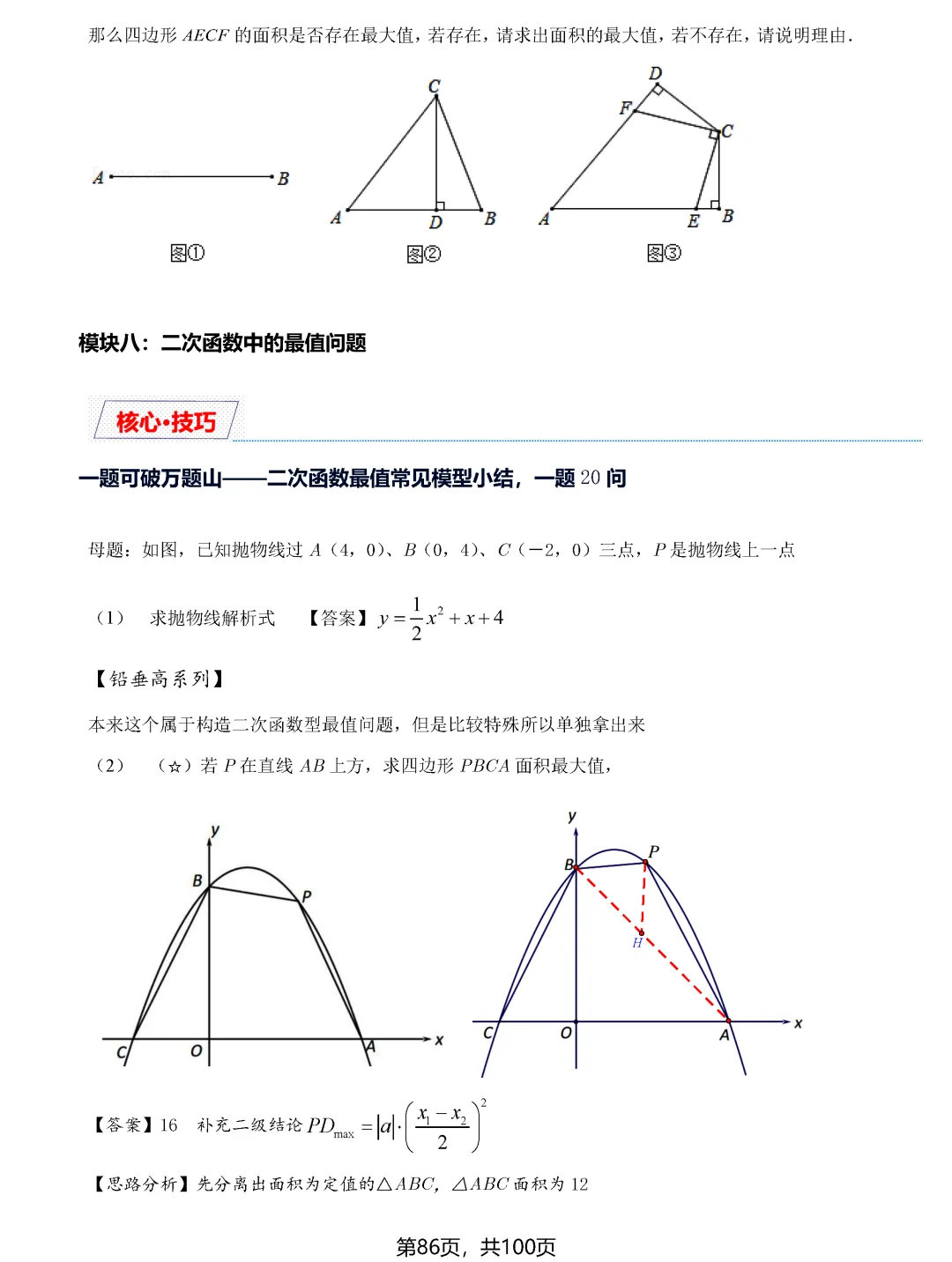
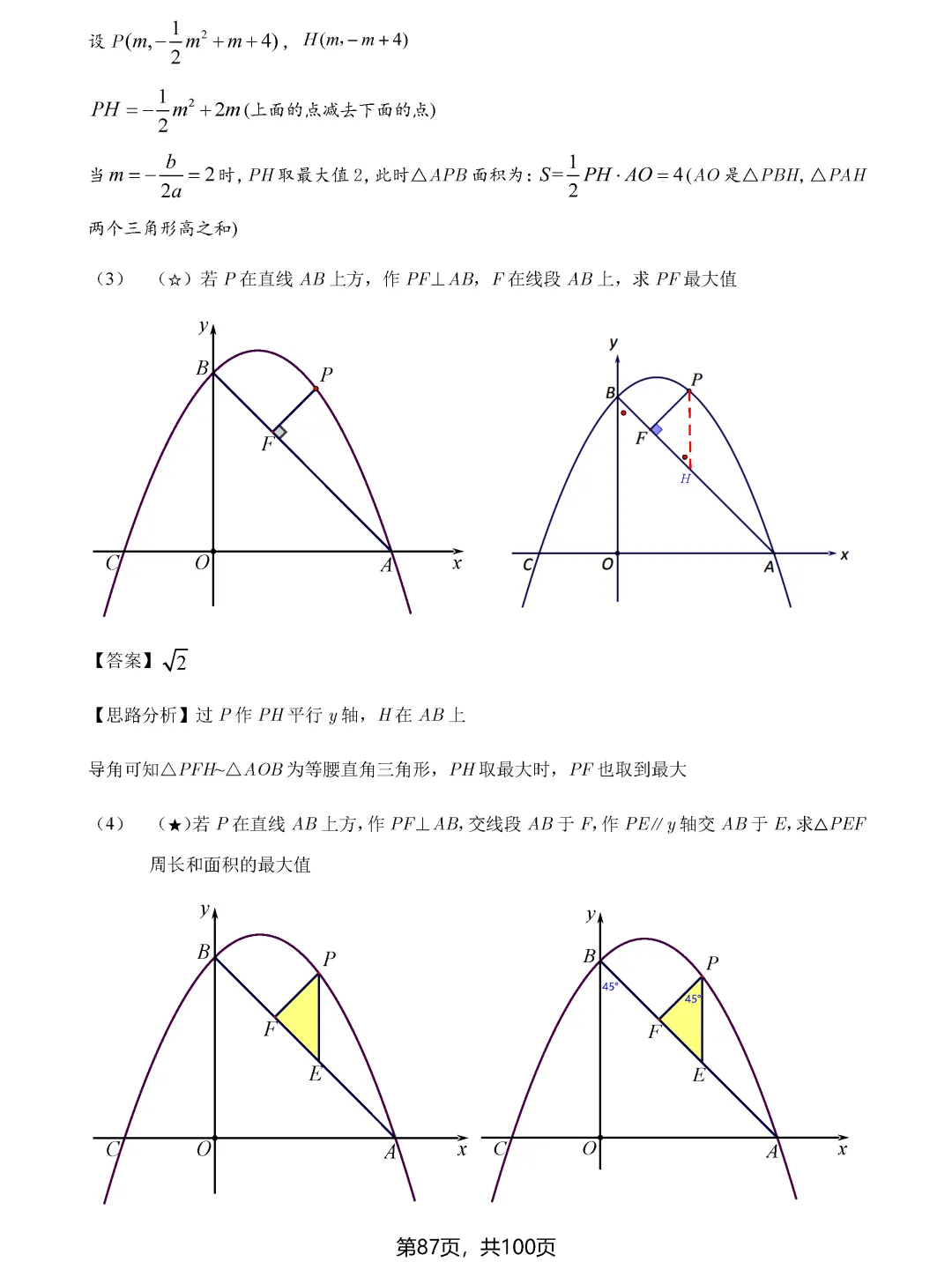
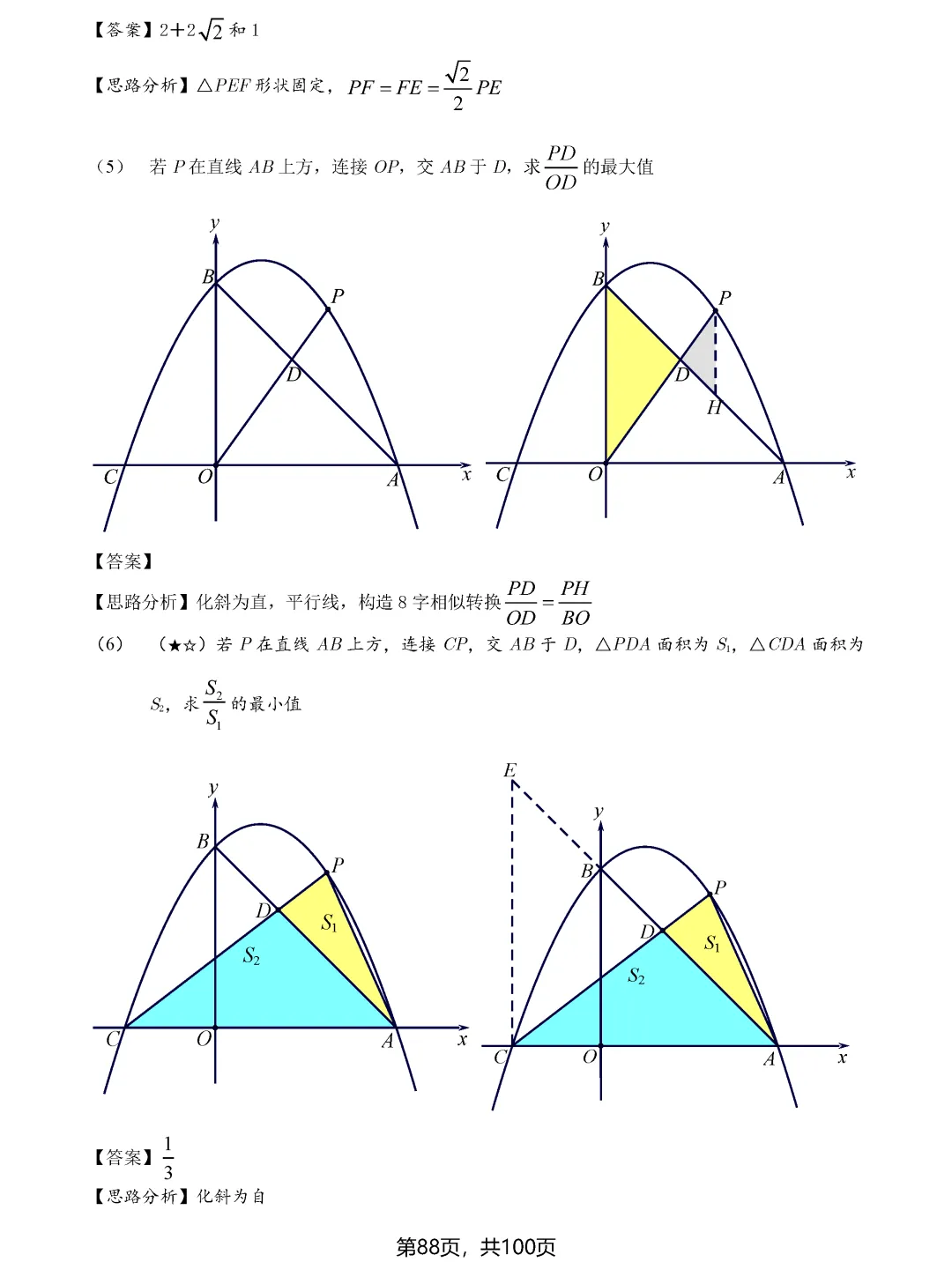
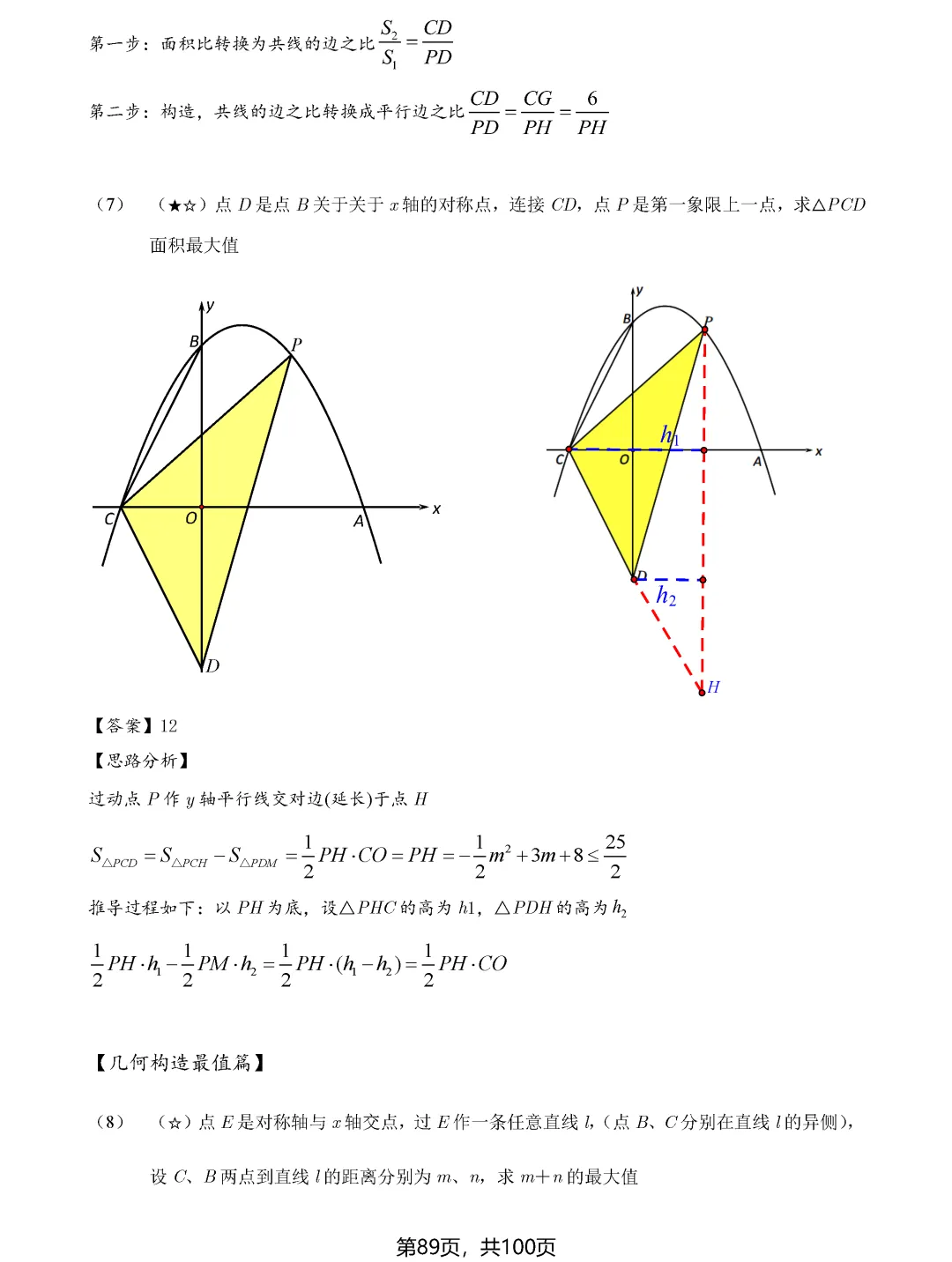
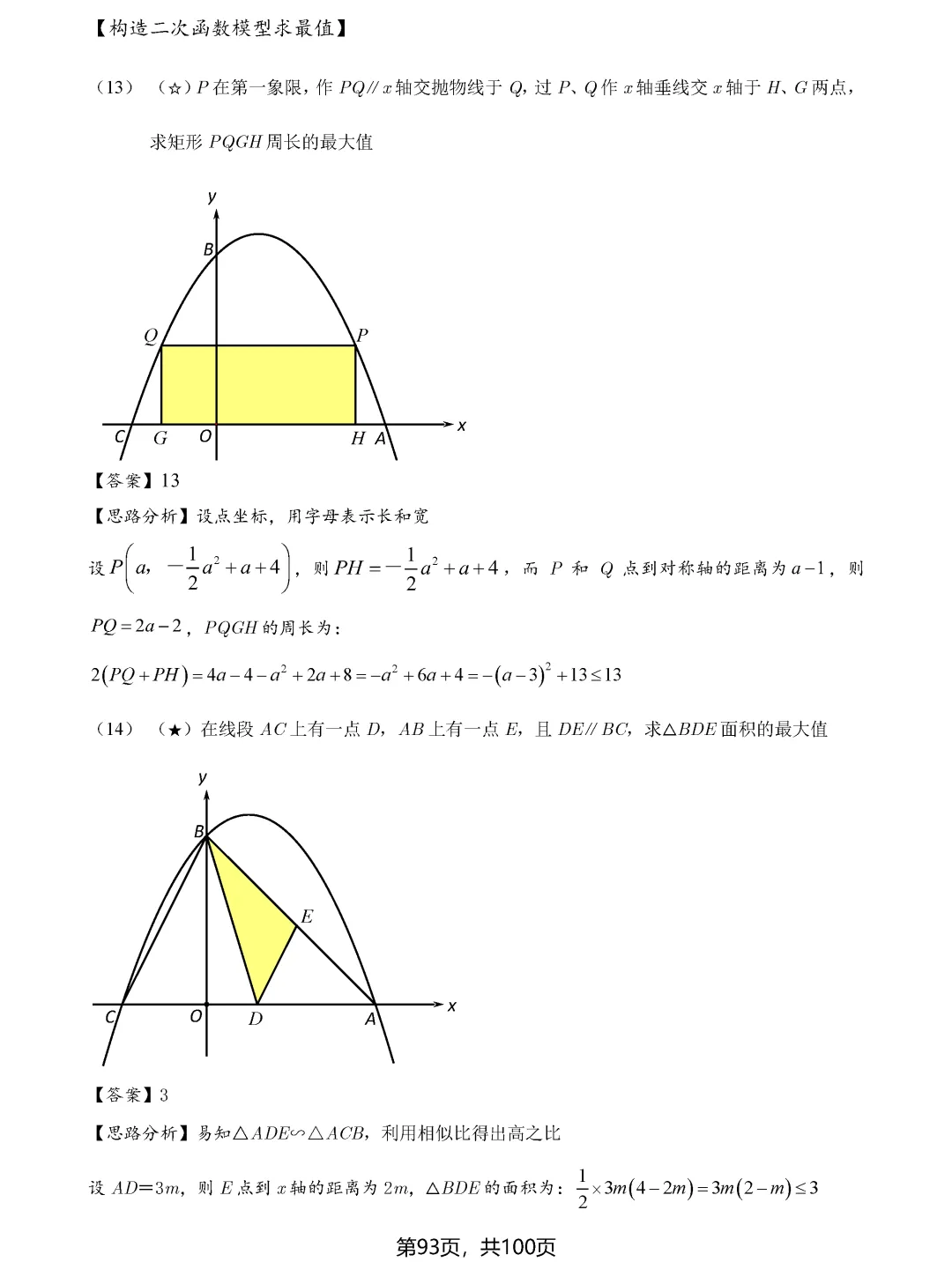
二次函数中的最值问题则偏向代数方法,通过建立函数模型,利用配方法或顶点公式求最值。但即便是代数问题,也常常需要结合几何意义,比如铅垂高最大、面积最大等问题,都需要数形结合才能快速解决。
最值问题的学习不能死记硬背,而要理解每个模型背后的数学原理。建议同学们在掌握基本模型后,多做变式训练,培养模型识别能力和构造能力。中考在即,系统梳理这八大类最值问题,定能在考场上游刃有余,拿下压轴题的高分。