中考数学提分:反比例函数k的几何意义

【中考数学提分：反比例函数k的几何意义】

反比例函数的解析式为y =k/x（ k≠ 0 ），其中常数 k不仅决定了函数的增减趋势，更蕴含丰富的几何意义。  

从图像上看，反比例函数的图象是双曲线，两支分别位于第一、三象限或第二、四象限，具体位置由 k 的符号决定。当k > 0 时，双曲线分布在第一、三象限；当  k < 0 时，双曲线分布在第二、四象限。  

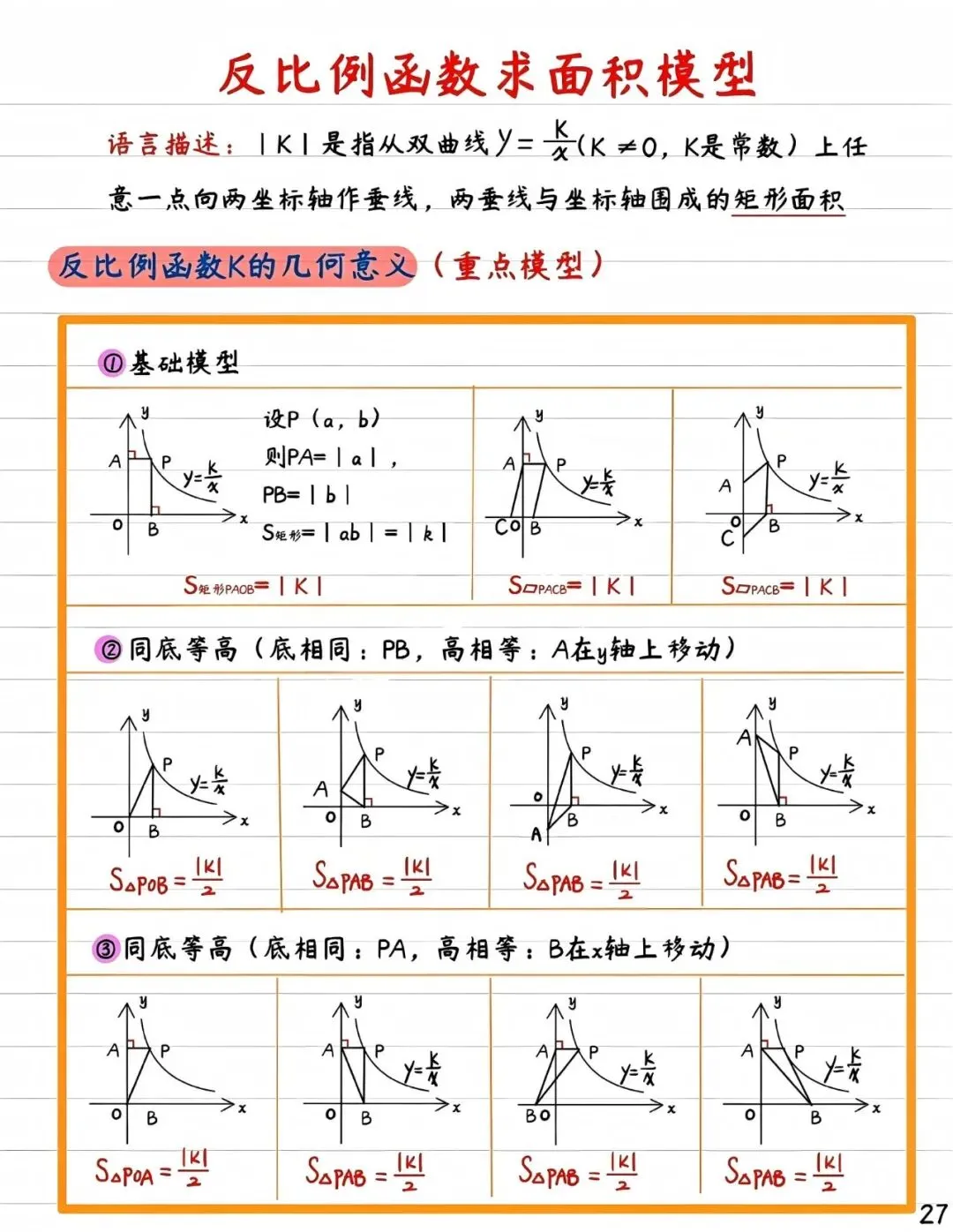
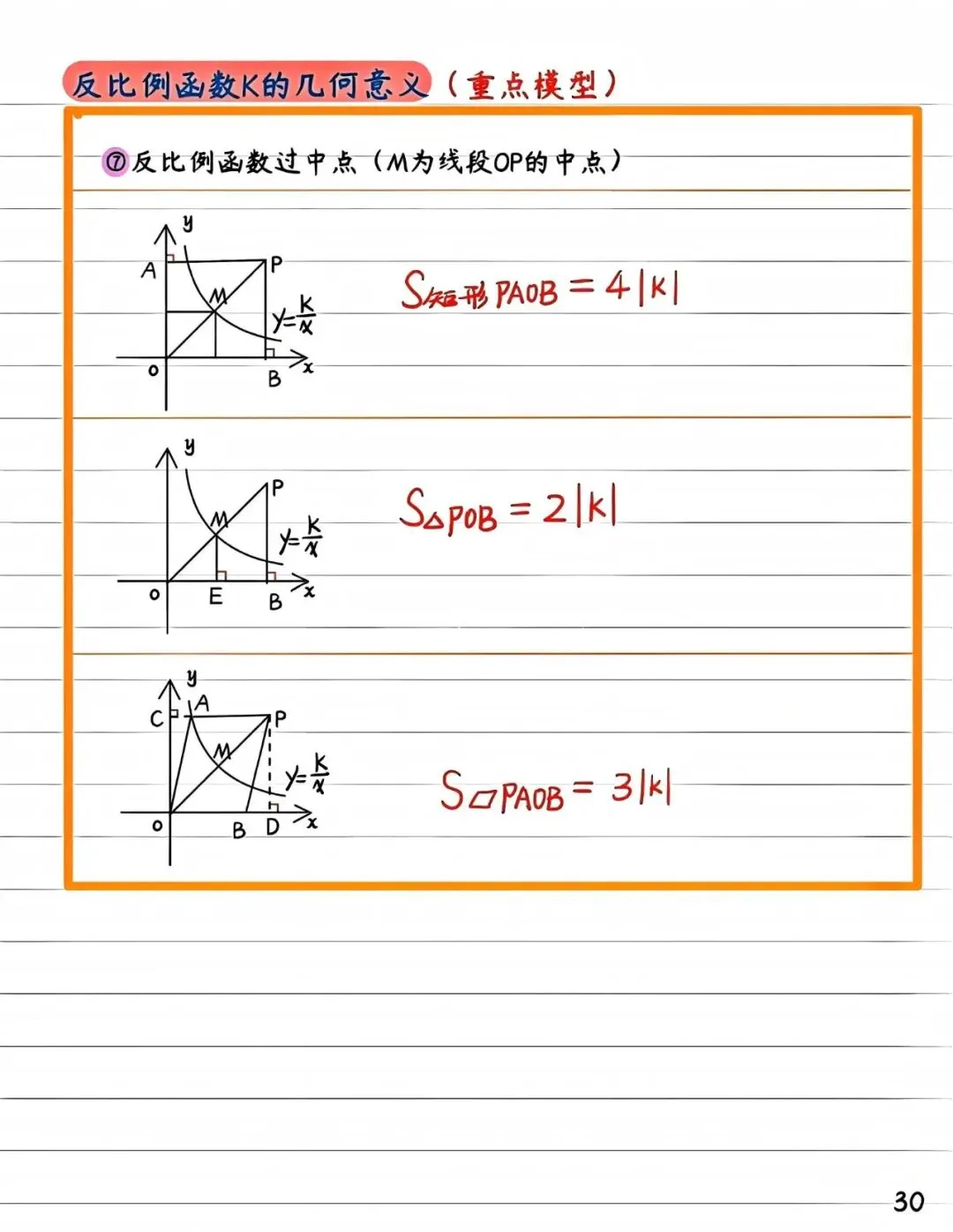
1. 矩形面积与k的关系

在双曲线上任取一点P(x, y) ，过该点分别作 x 轴和  y  轴的垂线，与坐标轴围成的矩形面积为 |xy| 。由于y = k/x，因此矩形的面积恒等于 |k| 。这一性质表明，无论点P在双曲线的哪个位置，其所形成的矩形面积始终不变，体现了 k的几何稳定性。  

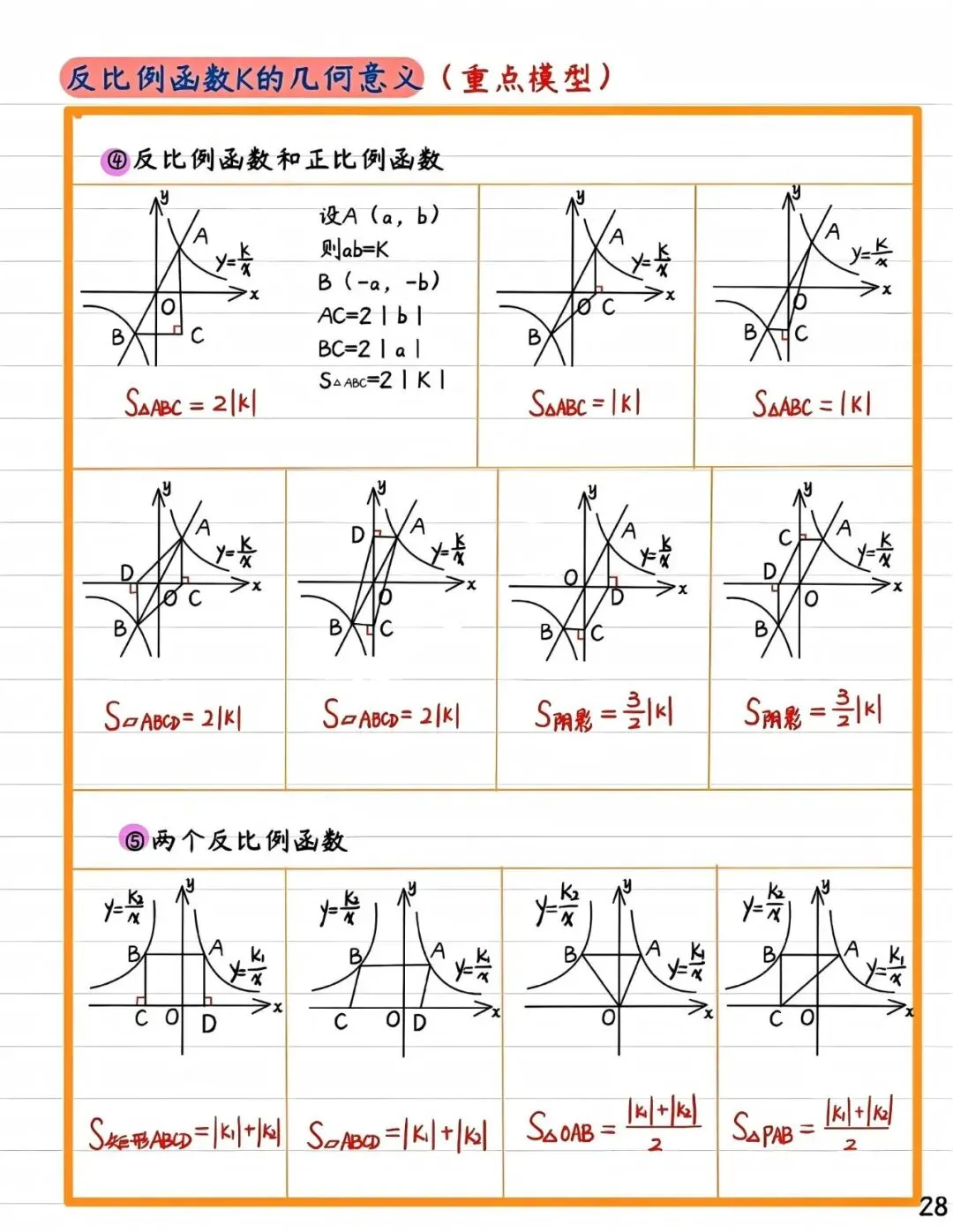
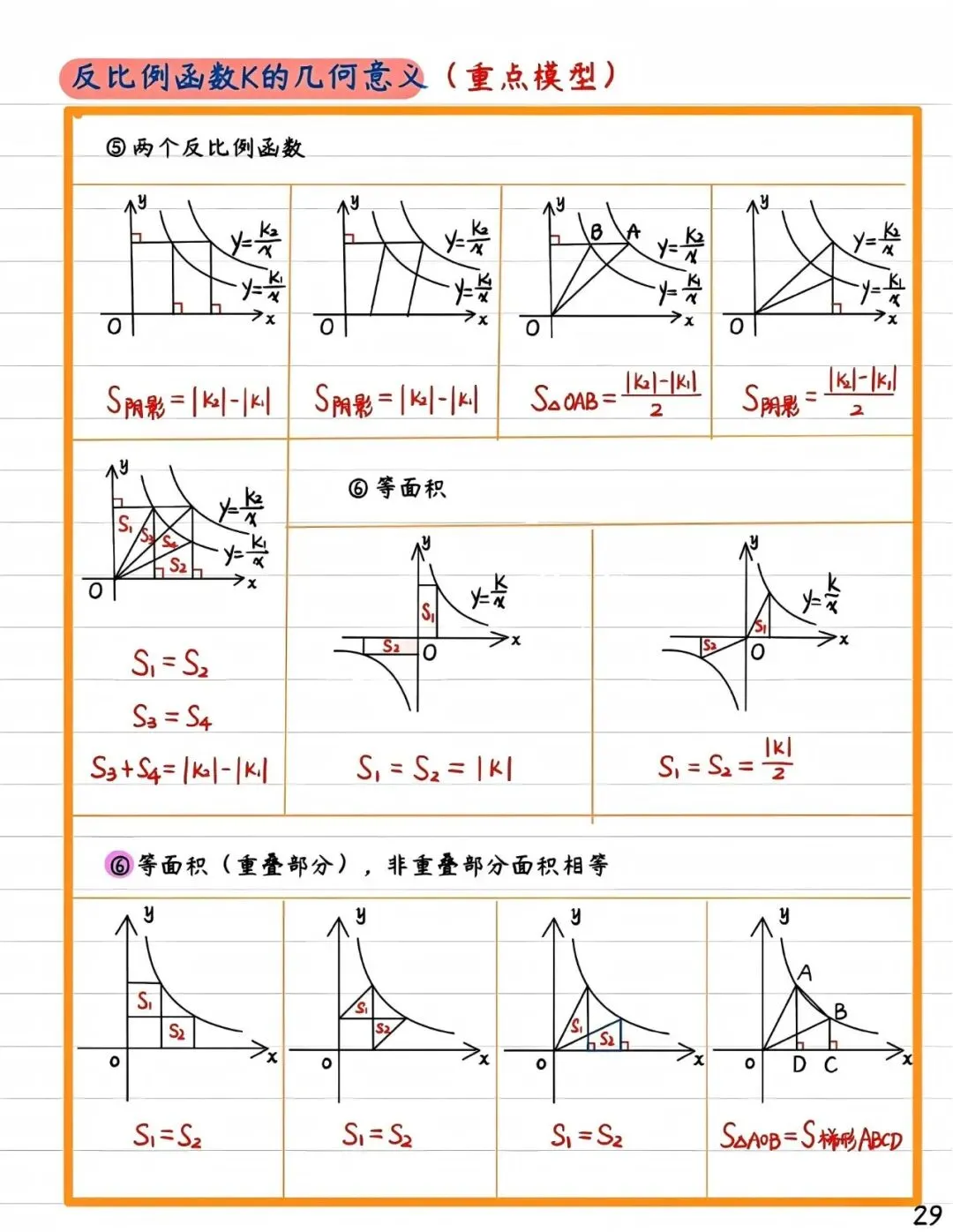
2. 三角形面积与k的关系

若连接点 P 与坐标原点 O ，并过 P点作 x  轴或 y 轴的垂线，可形成直角三角形。例如，设垂足为A(x, 0)，则三角形OAP的面积为|k| /2。这说明，反比例函数图象上的点与原点构成的三角形面积同样由k 决定，且为定值。  

3. 渐近线与k的关系 

双曲线的两支无限接近坐标轴，但永不相交，坐标轴即为双曲线的渐近线。虽然 k 不直接影响渐近线的位置，但它决定了双曲线的开口大小和弯曲程度。 |k|  越大，双曲线离原点越远，曲线形态更为舒展；反之， |k| 越小，双曲线越靠近原点，曲线显得更为紧凑。  

综上，反比例函数中的 k 不仅是解析式中的比例系数，更在几何上表现为双曲线与坐标轴围成的封闭图形的面积，以及曲线的分布特征。理解 k 的几何意义，有助于更直观地把握反比例函数的性质，为后续学习奠定坚实基础。