第三章 函数(文章最后有电子版资源供大家免费下载)
第一节 3. 2一次函数 - 考点知识梳理
考点一 一次函数的定义
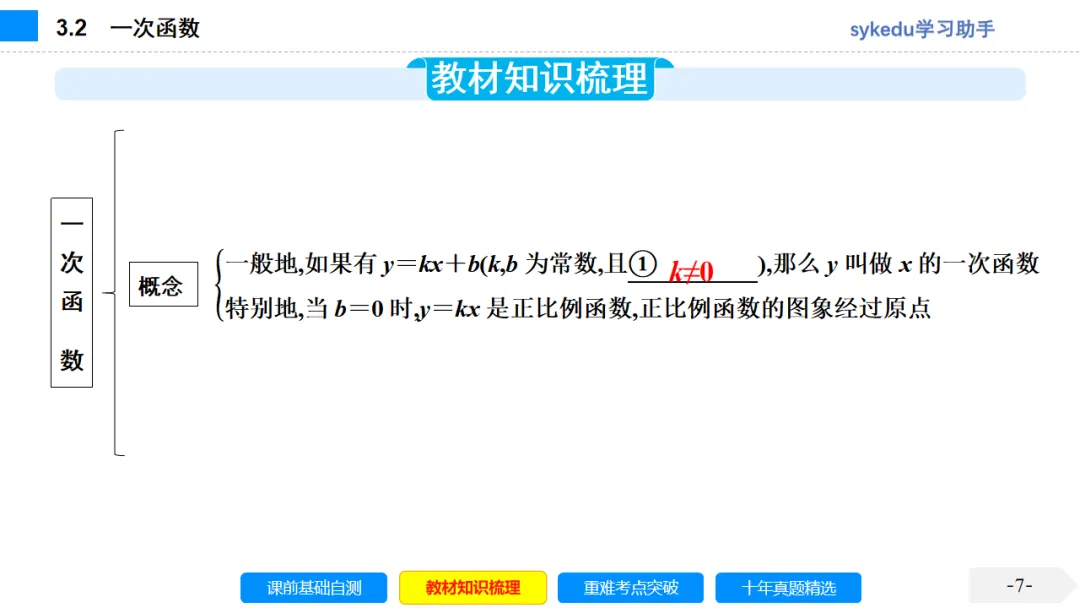
一般地,如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.
特别地,当b=0时,一次函数y=kx+b就成为y=kx(k是常数,k≠0),这时,y叫做x的正比例函数.
温馨提示
正比例函数是一次函数,但一次函数y=kx+b(k,b是常数,k≠0)不一定是正比例函数,只有当b=0时,它才是正比例函数.
考点二 一次函数的图象
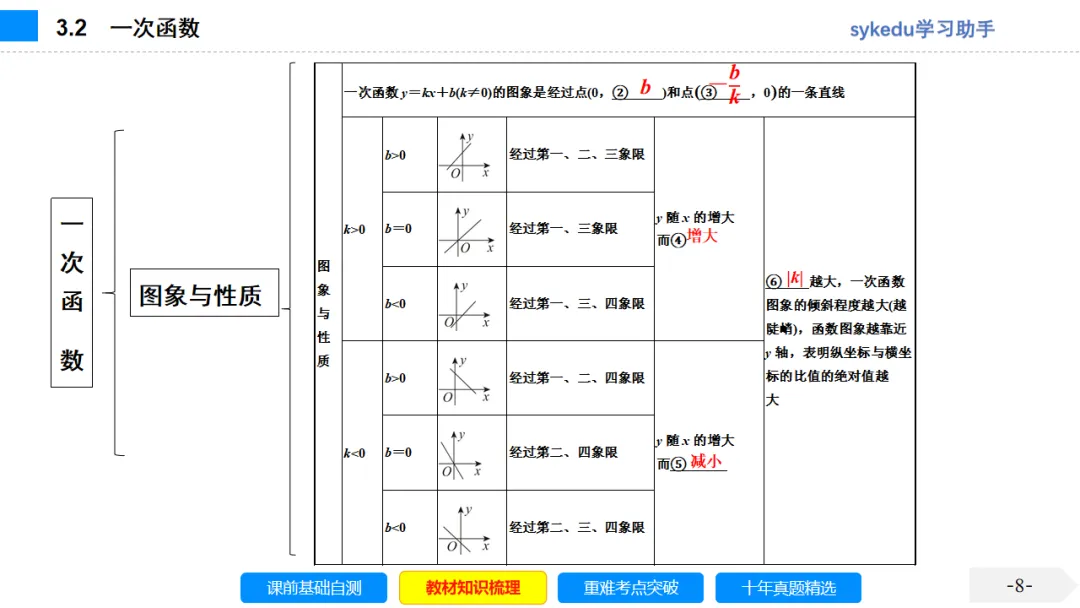
1.一次函数y=kx+b(k,b是常数,k≠0)的图象是一条过(0,b),(-k,0)的直线.
2.正比例函数y=kx(k≠0)的图象是一条过 (0,0)的直线.
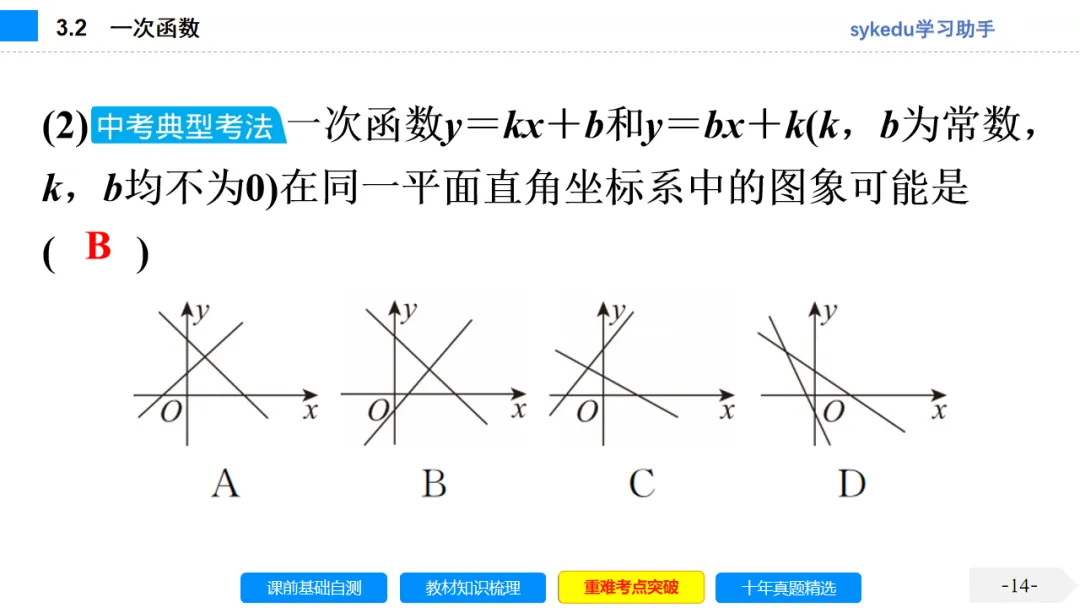
3.一次函数y=kx+b(k,b是常数,k≠0)的图象与k,b符号的关系
温馨提示
直线y=kx+b的位置由k和b的符号决定,其中b是截距(截距不是距离,是直线与y轴交点的纵坐标).(1)k决定直线从左至右呈上升趋势还是呈下降趋势:当k>0时,直线呈上升趋势;当k<0时,直线呈下降趋势.(2)b决定直线与y轴的交点的位置:当b>0时,交点在y轴的正半轴上;当b=0时,交点是原点;当b<0时,交点在y轴的负半轴上.
4.两条直线的位置与系数的关系
设直线l1与l2的解析式分别为l1:y1=k1x+b1,l2:y2=k2x+b2,则它们的位置关系可由系数决定:
(1)k1=k2,b1≠b2⇔l1与l2平行;
(2)k1=k2,b1=b2⇔l1与l2重合;
(3)k1·k2=-1⇔l1与l2垂直.
温馨提示
当直线y1=k1x+b1与y2=k2x+b2,当k1=k2,b1≠b2时,两条直线平行,这样的两条直线可通过平移得到.
考点三 一次函数的性质
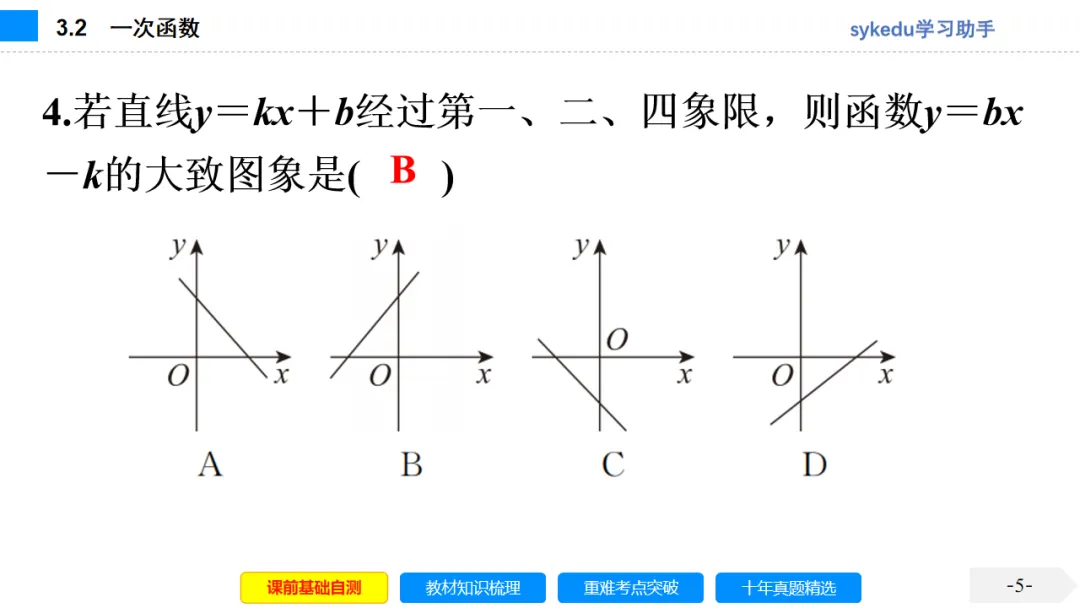
一次函数y=kx+b,当k>0时,y随x的增大而增大,图象一定经过第一、三象限;当k<0时,y随x的增大而减小,图象一定经过第二、四象限.
考点四 待定系数法求一次函数解析式
用待定系数法求一次函数解析式的一般步骤
(1)设出含有待定系数的函数解析式y=kx+b;
(2)把两个已知条件(自变量与函数的对应值)代入解析式,得到关于系数k,b的二元一次方程组;
(3)解二元一次方程组,求出待定系数k,b;
(4)将求得的待定系数的值代入 y=kx+b.
考点五 用函数观点看方程(组 )与不等式
1.一次函数与一元一次方程:求自变量x为何值时,一次函数y=ax+b的值为0⇔解方程ax+b=0.
2.一次函数与一元一次不等式:(1)解不等式ax+b>0⇔求自变量x在什么范围内,一次函数y=ax+b的值大于0;(2)解不等式ax+b<0⇔求自变量x在什么范围内,一次函数y=ax+b的值小于0.
3.一般地,每个二元一次方程组都对应两个一次函数,于是也对应两条直线.从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线交点的坐标.
温馨提示
函数值y>0时对应函数的图象在x轴上方;y<0时对应函数的图象在x轴下方.
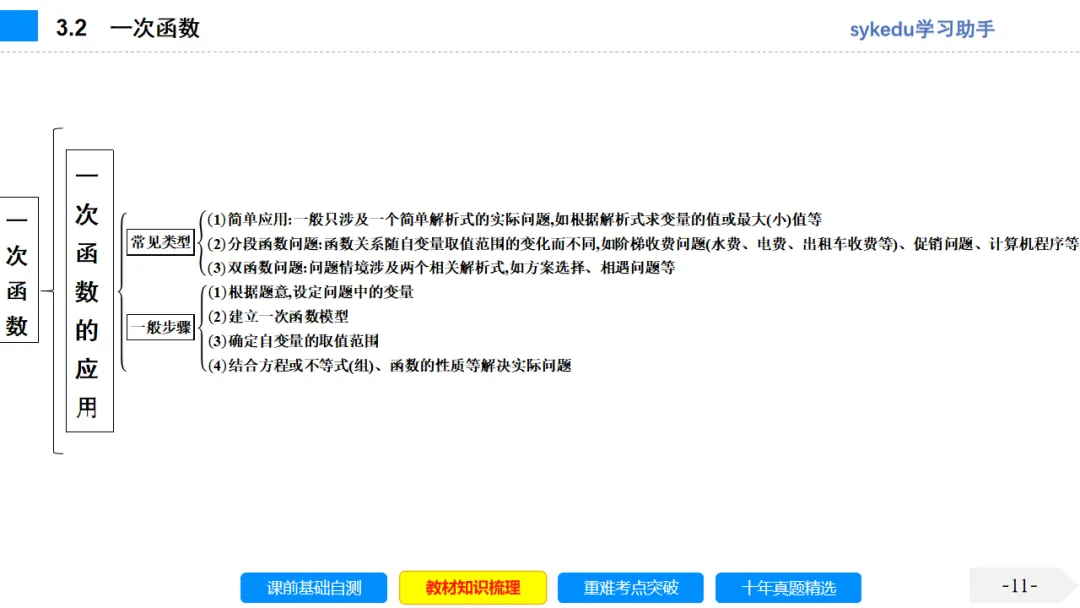
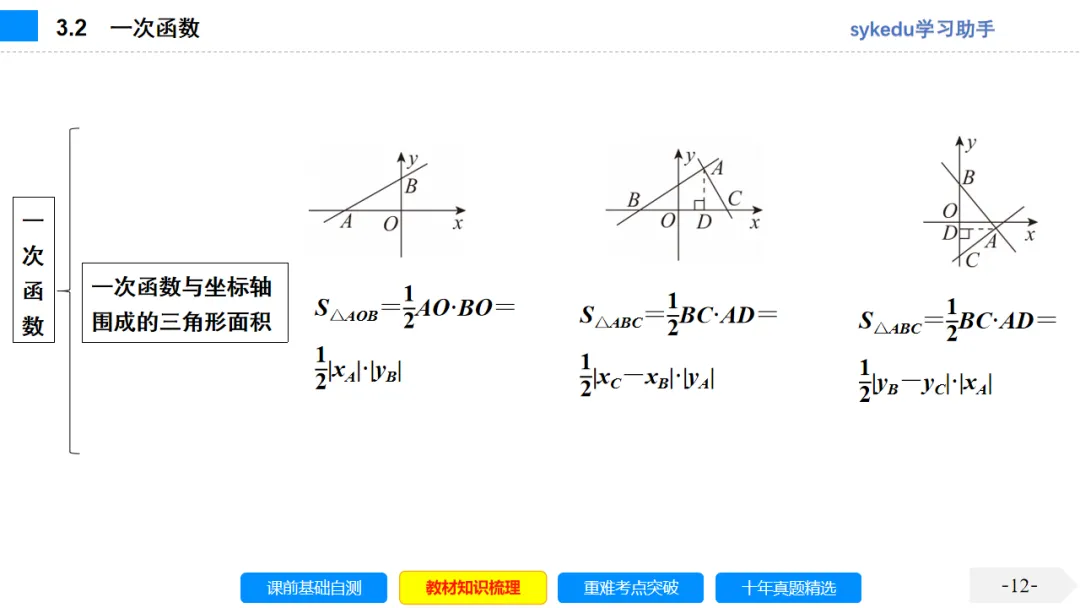
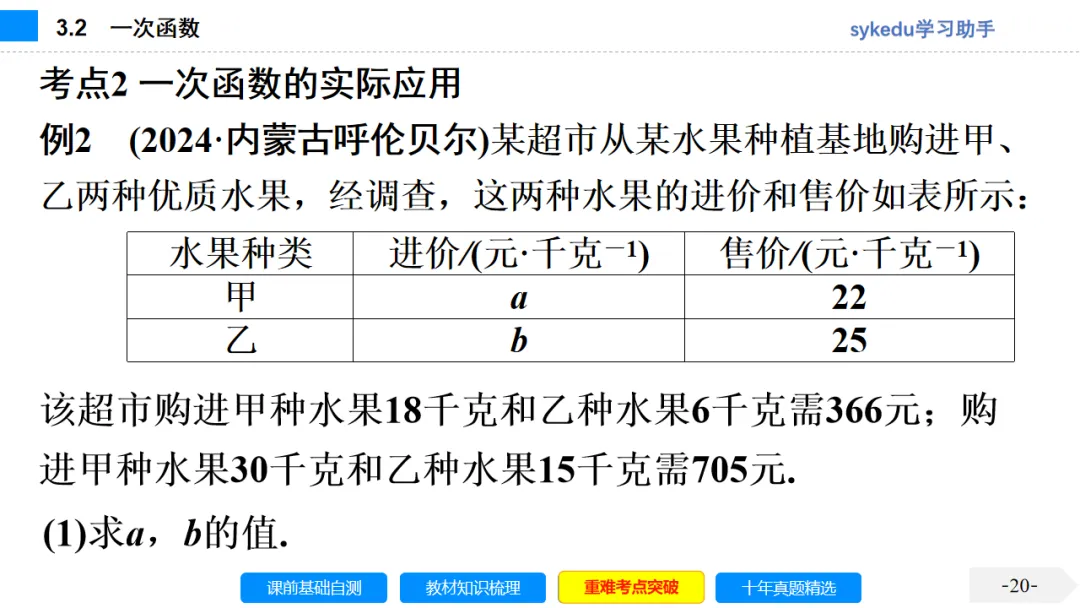
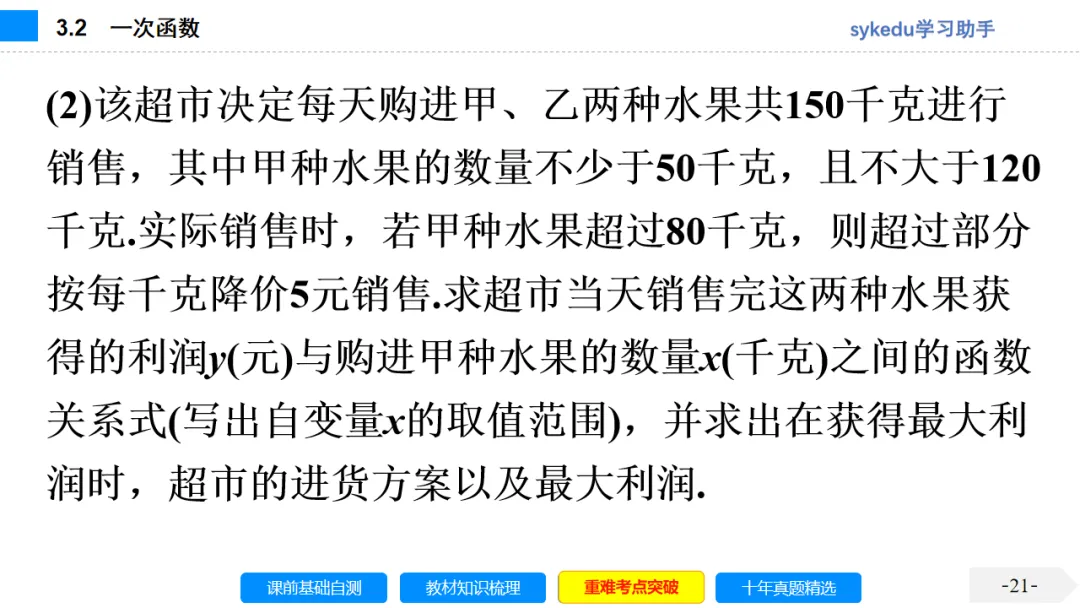
考点六 一次函数的应用
1.用一次函数解决实际问题的一般步骤:(1)设定实际问题中的变量;(2)建立一次函数关系式;(3)确定自变量的取值范围;(4)利用函数性质解决问题;(5)答.
2.一次函数的应用有如下常用题型
(1)根据实际问题中给出的数据列相应的函数解析式,解决实际问题;
(2)利用一次函数对实际问题中的方案进行比较;
(3)结合实际问题的函数图象解决实际问题.
温馨提示
运用一次函数的有关知识解决实际问题的关键是结合方程、不等式的有关知识求解,在确定一次函数的解析式时,要注意自变量的取值范围应受实际条件的限制.















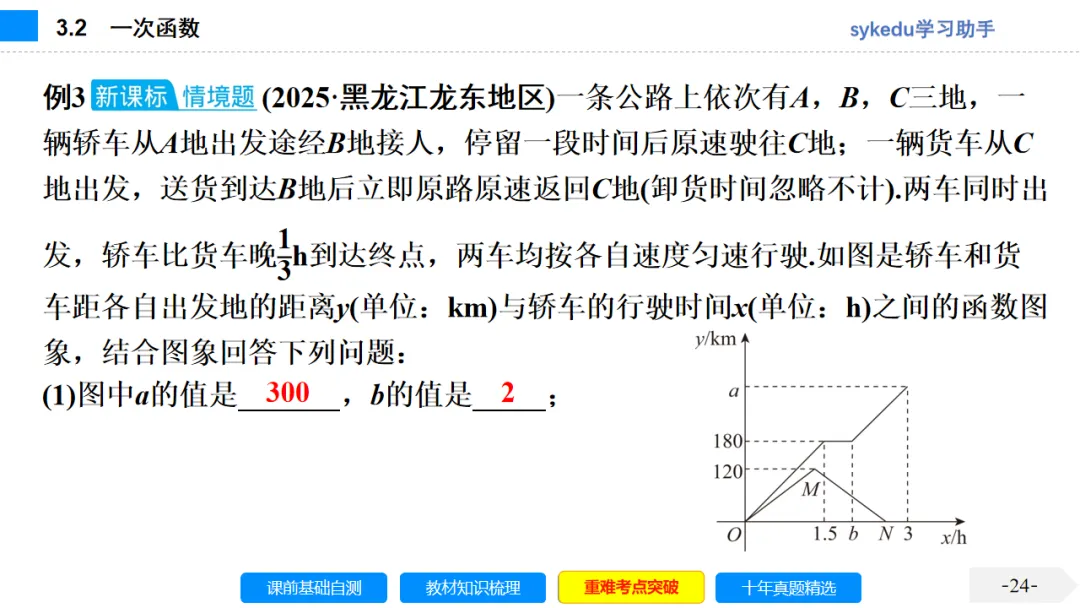



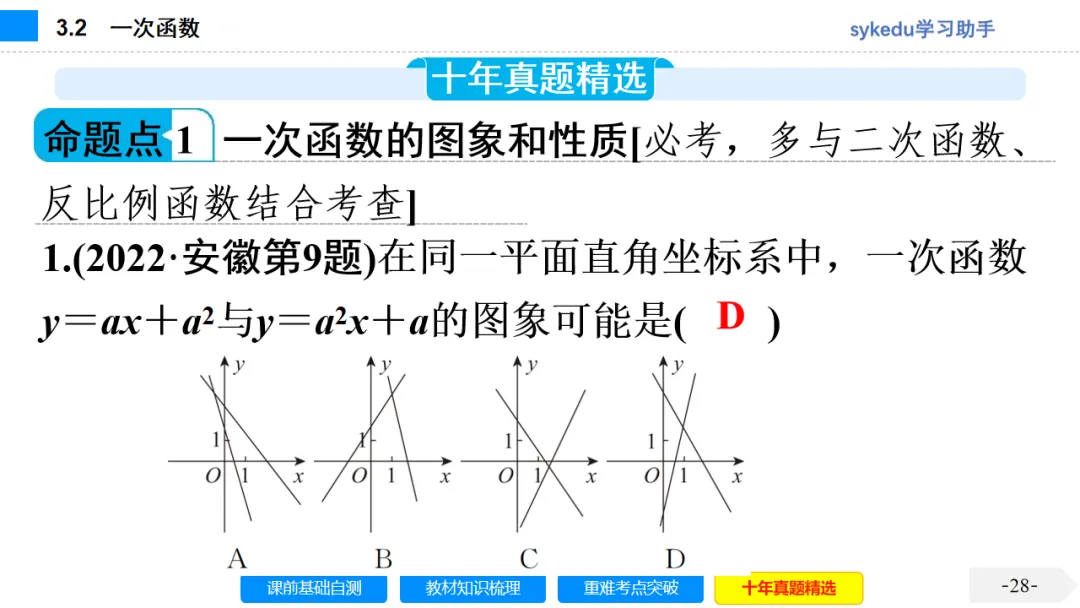

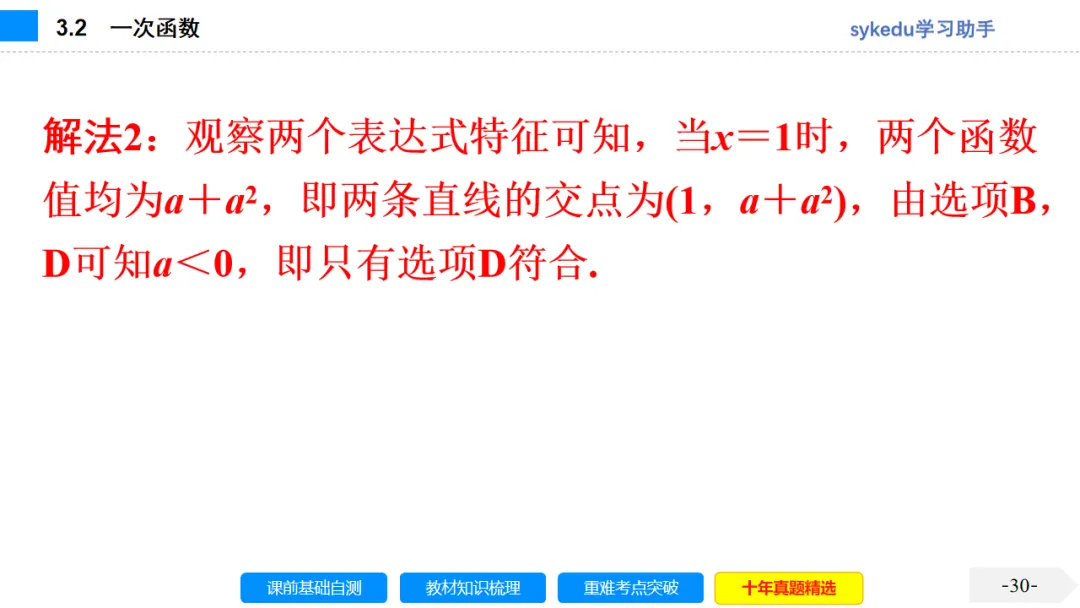




3.1 平面直角坐标系与函数-sykedu学习助手.pptx
3.4 第1课时 二次函数的图象与性质-sykedu学习助手.pptx
3.4 第2课时 二次函数性质的综合应用-sykedu学习助手.pptx






