(48)2025年重庆市中考
奉节县一模数学第26题
在△ABC中,∠ABC=90°, AB=BC=12,
点E,F分别为边AB,BC上的动点,
BD⊥AC交AC于点D,连接AF交BD于
点G .
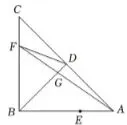
图1
(1)如图1,连接DF,若AB=3CF,
求△CDF的面积,
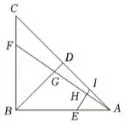
图2
(2)如图2,若BE=BF,作EH⊥AF交
AF于点H,交AC于点I ,
求证:AI=2DG,
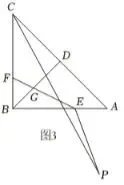
图3
(3)如图3,若BE+BF=AB,连接EF,
并将EF绕点E逆时针旋转135°至EP,
连接CP ,直接写出CP的最小值.
【解答】(1)如图4,取BC的中点H,
连接DH ,
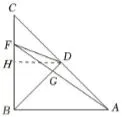
图4
∵ AB=BC,BD⊥AC ,
∴CD=AD .
∵∠ABC=90°,
∴CD=BD=1/2AC ,
同理可得,
DH⊥BC,
DH=1/2BC=6,
∵AB=12,AB=3CF ,
∴ CF=4,
∴ S△CDF=1/2CF·DH
=1/2x4x6
=12,
(2)如图5,延长AF至Q ,使GQ=AG,
连接CQ ,
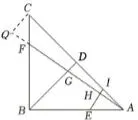
图5
由⑴可知:
AD=CD , BD⊥AC ,
∴CQ=2DG,
CQ//BD ,
∴ QC⊥AC .
∴∠ACQ=90°,
∵AB=BC ,
∠ABC=90°,
∴∠BAC=∠ACB=45°,
∴∠FCQ=∠ACQ-∠ACB
=90°-45°
=45°,
∴∠BAC=∠FCQ ,
∵BF=BE ,
∴BC-BF=AB-BE ,
∴CF=AE .
∵EH⊥AF ,
∴∠EHF =90°,
∴∠ABC+∠EHF=90°+90°
=180°,
在四边形BEHF中,
∠BFH+∠BEH=360°-(∠ABC+∠EHF)
=180°,
∵∠AEH+∠BEH=180°,
∴∠BFH=∠AEH ,
∵∠CFQ=∠BFH ,
∴∠CFQ=∠QEH,
∴△CFQ≌△AEI (ASA),
∴Al=CQ=2DG,
(3)如图6,连接DE, DF,
作DW⊥BC于W ,作DV⊥AB于V,
并延长至X ,使VX=√2DV,
过点V 作AB的平行线L,延长BC交L于
点P ,
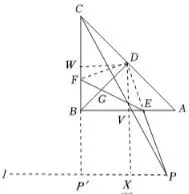
图6
当点F在点W处时, E点在V处,
VX=6√2,
∵AB=BC ,
∵ BE+BF=AB ,
AB=AE+BE ,
∴BF=AE ,
∵∠CBD=∠A=45°,
BD=AD ,
∴△BDF≌△ADE (SAS),
∴DF=DE , ∠BDF=∠ADE ,
∴∠BDF+∠BDE=∠ADE+∠BDE,
∴∠EDF=∠ADB=90°,
∴∠DEF=∠DFE=45°,
∴EF=√2DE,
∵EF绕点E逆时针旋转135°至EP ,
∴∠FEP=135°, PE=EF ,
∴∠DEF+∠FEP=180°,
PE=√2DE,
∴D,E,P共线,
∵DV/VX=DE/DP,
∴ DV/DX=DE/DP,
∵∠EDV=∠PDX ,
∴△DEV∽△DPX ,
∴∠DEV=∠DPX .
∴EV//PX .
∴点P在过点X且与 AB 平行的
直线上运动,
当点P在P处时,
CP最小值=BC+BP
=BC+VX
=12+6√2 .
往期文章






