
全国各地中考数学试题压轴几何综合题,图形背景来源教材,以数学《新课程标准》为纲领,充分体现出《中考说明》的相关要求。这种题一般设置了三问:(1)证明推断;(2)类比探究;(3)拓展应用,关注了对数学核心内容、基础知识、基本技能、数学思想与方法等多方面内容的考察,比较符合学情,能够体现出学生的几何书写,符号意识以及数学知识的迁移能力,同时具备一定的区分度,引领以后的中考备考。在证明推断中几何证明题重点考察的是学生的逻辑思维能力,能通过严密的“因为”、“所以”逻辑将条件一步步转化为所要证明的结论。
这类题目出法相当灵活,不像代数计算类题目容易总结出固定题型的固定解法,而更看重的是对重要模型的总结、常见思路的总结。所以对中考中最常出现的若干结论做了一个思路总结。
一、证明两线段相等
1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等(平行线等分线段定理)。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。
11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
12.等于同一线段的两条线段相等或者等量代换。
例题1:如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.求证:BE=CF;
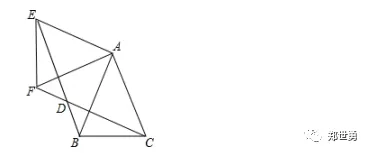
【试题分析】先由旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CD;
【解答】证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF;
【试题点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等。
二、证明两角相等
1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。
7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。
8.相似三角形的对应角相等。
9.圆的内接四边形的外角等于内对角。
10.等于同一角的两个角相等。
例题2:如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
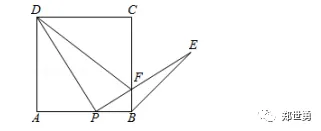
【试题分析】(1)根据∠ADP与∠EPB都是∠APD的余角,根据同角的余角相等,即可求证;
(2)首先证得△PAD≌△EQP,可以证得△BEQ是等腰直角三角形,可以证得∠EBQ=45°,即可证得∠CBE=45°;
【解答】(1)证明:∵四边形ABCD是正方形.
∴∠A=∠PBC=90°,AB=AD,
∴∠ADP+∠APD=90°,
∵∠DPE=90°,
∴∠APD+∠EPB=90°,
∴∠ADP=∠EPB;
(2)解:过点E作EQ⊥AB交AB的延长线于点Q,则∠EQP=∠A=90°,
又∵∠ADP=∠EPB,PD=PE,
∴△PAD≌△EQP,
∴EQ=AP,AD=AB=PQ,
∴AP=EQ=BQ,
∴∠CBE=∠EBQ=45°;
【试题点评】本题主要考查了正方形的性质,以及三角形相似的判定与性质,正确探究三角形相似的性质是解题的关键。














三点建议:
1.必须重视基础知识的掌握和基本技能的训练,特别是基本概念定理的教学。应该重视知识的形成过程,把探索的过程留给学生,让学生通过自主活动,自我建构,进而达到对数学知识的真正理解,并注意揭示知识与知识之间的内在联系,归纳、提炼和总结蕴含在知识内的数学思想方法,帮助学生形成合理的认知结构。
2.同时还要渗透对数学能力的培养,不但要加强运算能力、思维能力、空间观念以及分析问题和解决问题能力的培养,而且还要注意分析处理信息能力、探究发现能力以及数学运用意识的培养和训练,逐步发展学生的探索能力和创新能力。
3.平时要严格要求学生,让他们养成良好的学习习惯和书写习惯。从试卷来看,这方面存在的问题也不少,比如书写不工整,字母不对应,解题不规范等问题不断出现。这就要求教师在平时的教学中应该严格各方面的要求,使学生逐步养成良好的学习习惯和规范的书写习惯。







