点击上方“ 郑世勇工作室”关注我们
2021年襄阳市中考数学试题的第24题是纯几何综合题,图形背景来源教材,以数学《新课程标准》为纲领,充分体现出《中考说明》的相关要求。这几年的试题,主要题型呈现形式、题型设置、题目难度、考查要点、书写情况等方面没有作较大改动,保持连续性的基础上,部分问法的呈现形式进行了尝试性的创新,比如让学生体会从特殊到一般的转化思想,用特殊问题的解题方法去解决一般情况的问题,这些都体现了《中考说明》中要求的立足基础、渗透思想、突出能力、着眼发展的创新性。中考中关注了对数学核心内容、基础知识、基本技能、数学思想与方法等多方面内容的考察,特别对抽象意识,几何直观,推理能力,运算能力4个数学核心素养的综合考查,符合学情,能够体现出学生的几何书写,符号意识以及数学知识的迁移能力,同时具备一定的区分度,对中考备考有很大的参考价值。下面以几道例题加以说明。




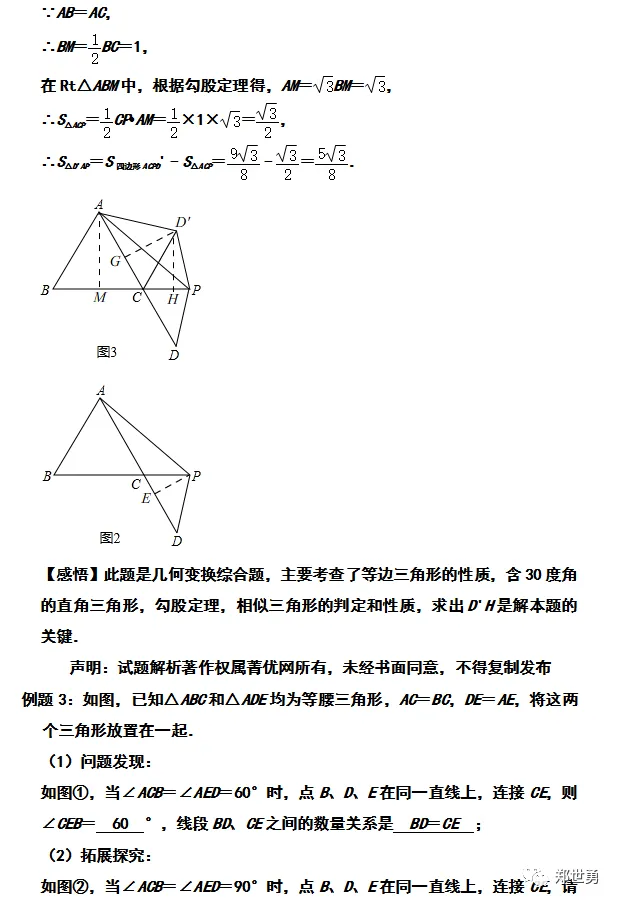



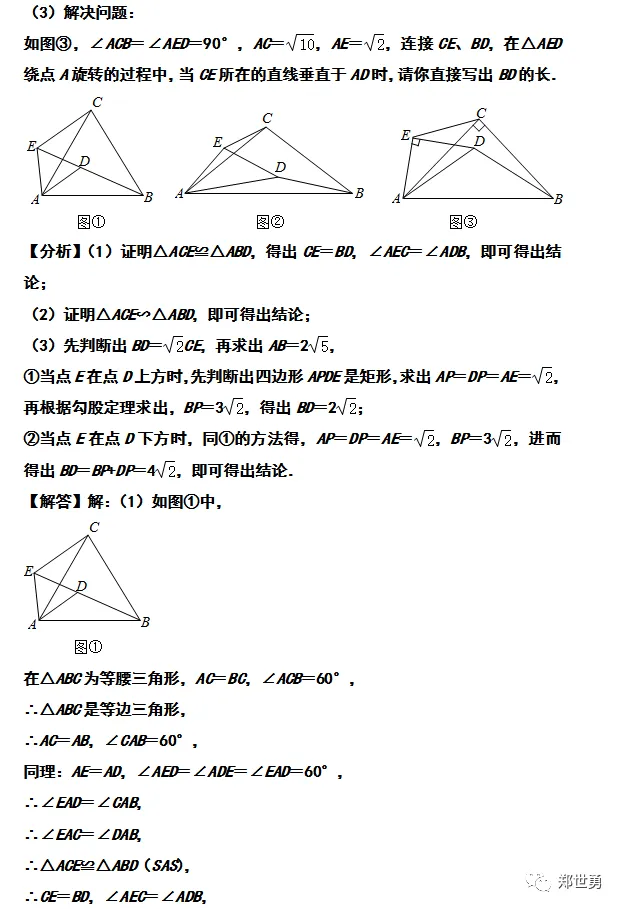


【感悟】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等边三角形的性质,判断出△ACE∽△ABD是解本题的关键。
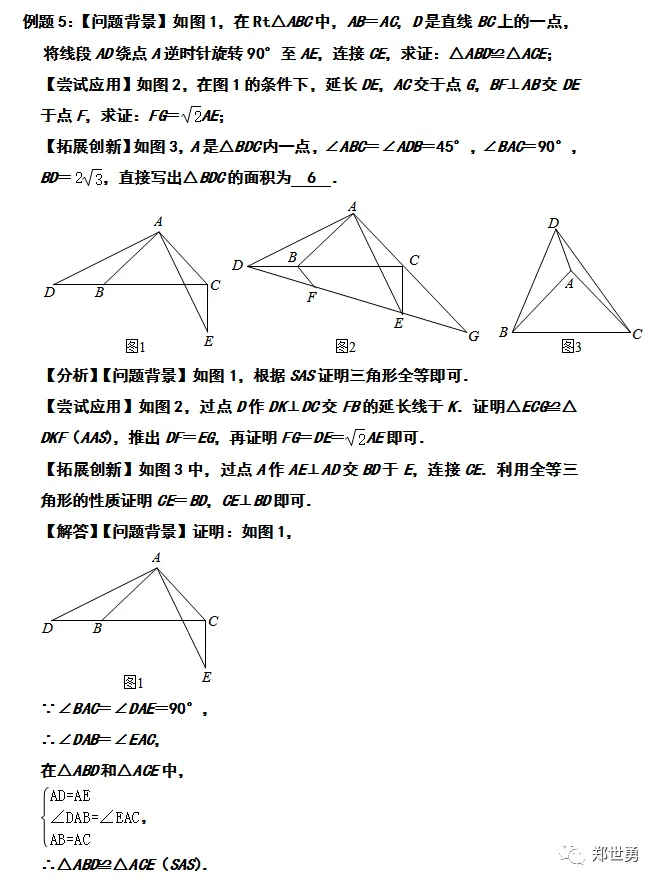





【感悟】本题属于相似形综合题,考查了旋转变换,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


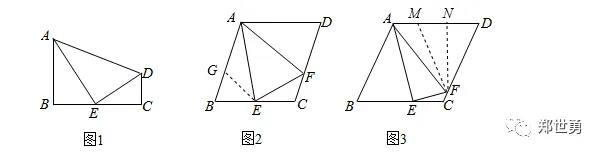
【感悟】本题主要考查三角形的相似,熟练掌握相似三角形的性质及判定方法是解题的关键。
当然后期还是要规范训练,注重习惯养成。试题的命制上注重科学性、规范性的体现:(1)语言规范:精准,严密等;(2)格式规范:数字,符号,图表,序号等;(3)结构合理:长度,题型、内容搭配;(4)情境适切:避免装饰性情境,虚假情境等;(5)难度适中;(6)表现形式:证明、探究、计算;(7)答案全面:表现性试题,开放性试题。试卷的方向决定着该地区教育的方向,试卷的质量决定着该地区教育的质量。同时平时要严格要求学生,让他们养成良好的学习习惯和书写习惯。从试卷来看,这方面存在的问题也不少,比如书写不工整,字母不对应,解题不规范等问题不断出现。这就要求教师在平时的教学中应该严格各方面的要求,使学生逐步养成良好的认真审题习惯、限时练习习惯、解后反思习惯、认真读书习惯、独立思考习惯、善于归纳习惯、合作研讨习惯、及时矫正习惯和验算检查习惯。
如此同时还要注意查漏补缺,注重反思总结。平时学习要强化理解易错题的正确解题思路,避免知识点的遗漏,更要注意获取“一题多解、多题一解、一题多变、一题多问、多题归一、老题新做”的方法和技巧,及时反思总结,构建思维的常规模式(掌握通法和策略)。






