(46)2025年天津市中考
红桥区一模数学第24题
在平面直角坐标系中,O为原点,
矩形OABC的顶点A在 x 轴的正半轴
上,D为边OA上一点,∠OCD=30°,
∠CDB=90°, OC=√3 .
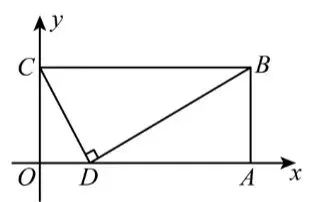
图1
(1)填空:如图1,点D的坐标为________,
点B的坐标为_________,
(2)将△ODC沿水平方向向右平移,得到
△O'D'C',点O, D, C的对应点分别为O',
D',C',设OO'=t,△O'D'C'与△DAB重
叠部分的面积为S .
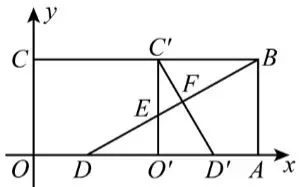
图2
①如图2,当△O'D'C'与△DAB重叠部分
为四边形时, C'O', C'D'与DB分别相交
于点E, F,试用含有t的式子表示S ,并
直接写出t的取值范围,
②当2≤t≤7/2时,求S的取值范围(直接写出结果即可) .
【解析】(1)∵矩形AOCB,
∴∠COD=∠BCO=90°,
AO=BC ,
在Rt△COD中,
∠COD=90°,
∠OCD=30°,
OC=√3,
∴OD=OC·tan30°
=√3x√3/3=1,
CD=OC/cos30°
=√3/(√3/2)
=2,
∴D(1,0),
∵∠BCO=90°, ∠OCD=30°,
∴∠BCD=60°,
在Rt△BCD中,
∠CDB=90°,
∠BCD =60°,
CD=2,
∴AO=BC=CD/cos60°
=2/(1/2)
=4,
∴B(4,√3),
故答案为:(1,0),(4,√3),
(2)①∵∠CDA=∠CDB+∠ADB
=∠COD+∠OCD ,
∠COD=∠BDC=90°,
∠OCD=30°,
∴∠ADB=∠OCD=30°,
∠CDO=60°,
∵平移,
∴DD'=OO'=t ,
∠C'D'O'=∠CDO=60°,
∴∠DFD'=90°,
∴DF= DD'·cos30°
=√3/2t,
D'F=DD'·sin30°=t/2,
在 Rt△DEO'中,
DO'=OO'-OD
=t-1,
∴EO'=DO'·tan30°
=√3/3(t-1),
∴当△O'D'C'与△DAB 重叠部分
为四边形时,
S=S△DD'F-S△EO'D
=1/2x√3t/2xt/2
-1/2(t-1)·√3/3(t-1)
=√3/8t²-√3/6(t²-2t+1)
=-√3/24t²+√3/3t-√3/6,
当D'和D重合时, t=1,
当D'和A重合时, t=4-1=3,
∴S=-√3/24t²+√3/3t-√3/6,
(1<t≤3),
②当2≤t≤3时,
由①知
S=-√3/24t²+√3/3t-√3/6
=-√3/24(t-4)²+√3/2,
∵-√3/24<0,
∴抛物线开口向下,
∴当t<4时,
S随t的增大而增大,
∵2≤ t ≤3
∴当t=2时,
S有最小值为
-√3/24x(2-4)²+√3/2
=√3/3,
当t=3时,
S有最大值为
-√3/24x(2-4)²+√3/2
=11√3/24,
∴ √3/3≤ S ≤11√3/24,
当3< t ≤7/2时,
如图3,
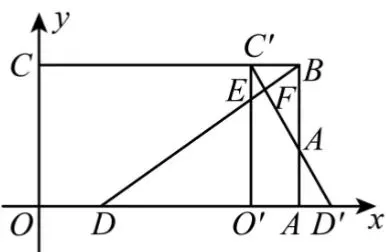
图3
在 Rt △AD'G中,
AD'=OD+DD'-OA
=t-3,
∴AG=AD'·tan60°=√3(1-3),
∴S=S△DD'F - S△DO'E - S△AD'G
=1/2x√3t/2·t/2
-1/2(t-1)·√3/3(t-1)
-1/2(t-3)·√3(t-3)
= -13√3/24t²+10√3/3t-14√3/3
=-13√3/24(t-40/13)²+6√3/13,
∵ -13√3/24<0,
∴抛物线开口向下,
∵40/13<7/2,
∴当t=40/13时,
S有最大值为6√3/13,
∵抛物线开口向下,
∴点到对称轴的距离越大,函数值越小,
∵l3-40/13l=1/13,
l7/2-40/13l=11/26,
1/13<11/26,
∴当t=7/2时,
S 有最小值为
-13√3/24·(7/2-40/13²+6√3/13
=35√3/96,
∴35√3/96≤ S ≤6√3/13,
综上所述,35√3/96≤ S ≤6√3/13 .
往期文章







