寒假为了保持清醒的头脑和做题手感,不至于业荒于戏变成“小年痴呆”,基本保持每天做一两题的习惯,偶得一好题,在此分享:
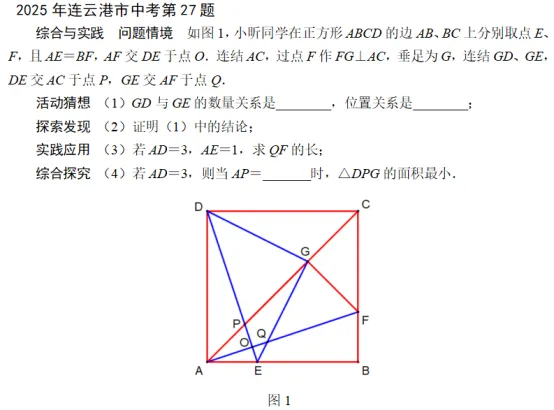
2025年连云港市中考数学试卷第27题,个人认为是非常棒的一道题,是区分考生水平的关键题目,有必要深入探究。题目设置遵循了“活动猜想”、“探索发现”、“实践应用”、“综合探究”的逻辑层次,引导学生在具体情境中发现问题、提出猜想、证明结论并应用于实际计算。不仅考察了学生对正方形基本性质的理解,更考察了学生对几何模型的灵活运用与综合解题能力。网上有不少关于此题的试题研究,我也希望通过自己的思考在此抛砖引玉。
以下这道题网络上、资料中流传的普遍参考答案:
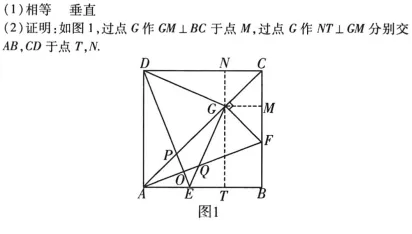

我仅就(4)问“综合探究”给出一种我的思考:
由∠PDG=45°,在正方形背景下,考虑“半角模型”解题可行性(半角模型此处不作详细探讨);
将线段DG顺时针旋转90°至线段DS,并连接AS、SP;不难证明△DGC≌△DSA,以及△DGP≌△DSP;
欲求△DGP面积的最小值,考虑到D点到PG所在直线的距离为定值,即求PG最小值,从而转化为求SP最小值;
∠SAD=∠DAP=45°,知△ASP为直角三角形,在Rt△ASP中:AS²+AP²=SP²
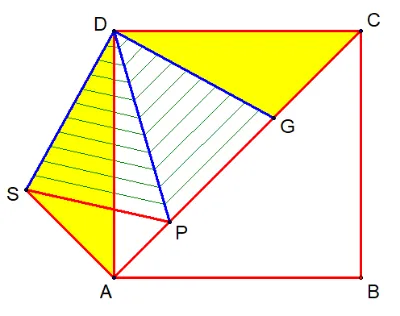
设AS=a,AP=b,有:a²+b²=SP²,由a²+b²≥2ab,当a=b时等号成立,即AS=AP时SP取得最小值√2a,于是AC=AP+GC+PG=2AP+SP=(2+√2)a=3,求出a值
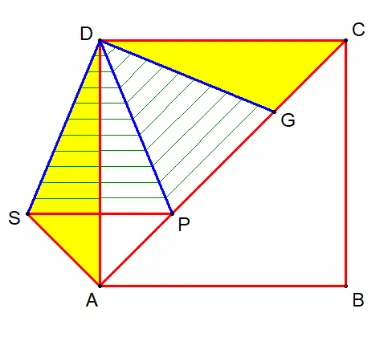
真是一道高质量的压轴题,它充分体现了新课程标准下问题情境化、思维层次化、知识综合化、素养导向化的命题方向,对于未来的考生而言,应对此类题目的关键在于夯实基础、注重思想以及提升能力(在复杂图形中分解基本图形、用代数方法解决几何最值问题的能力)。
真是一道不可多得的好题,值得我花时间和精力在课堂上认真评讲。如果从学生的角度出发,我更能接受“半角模型”这一做题方法;如果从题型角度出发(本题为填空题)我也更希望学生可以接受和掌握这一方法。因为它作为解决填空题型时较简单高效,这对于在考场上精神高度紧张的考生而言至关重要;而作为解答题型的解法,作图便利,过程书写顺畅,扣分点少。
窥一斑而见全豹,我斗胆对2026年中考数学命题趋势作以下判断:
2025年的这道压轴题反映了当前教育改革的方向,预计2026年的命题将在以下几个方面继续深化:
1. “综合与实践”可能成为压轴题的“固定主角”
情境更真实:题目背景可能不再局限于几何图形,而可能引入实际生活场景(如建筑设计、路径规划、资源分配)或跨学科情境(物理中的镜面反射、化学中的分子结构),要求学生用数学眼光观察并建模。
任务驱动:题目会通过“活动一、活动二”或“任务一、任务二”的形式,引导学生经历“发现问题—提出问题—分析问题—解决问题”的全过程。
2. “代数与几何的深度融合”仍是区分关键
第(4)问是最好的佐证,这种数形结合的思想落地将会是优等生与中等生的分水岭。
动态几何与函数:预计2026年会继续加强对动点问题的考查,要求学生能建立几何量之间的函数关系式,并利用函数性质(最值、增减性)求解。
路径与轨迹:对动点运动轨迹的探究可能会成为新的热点,考查学生的空间想象和逻辑推理。
3. “阅读理解与符号表达”能力要求提高
我查阅了不少省市2025年中考真题和模拟题,有相当一部分题目图形复杂、线条众多。2026年增加文字阅读量、精准识别基本几何模型或引入新定义这些趋势只会“愈演愈烈。
文中思之甚浅,囿于篇幅,还有很多值得探讨的“点”没有展开,比如前文谈到的“半角模型”、“基本不等式”等,每一个“点”单拎出来都是可以大书特书的篇章,这更进一步说明了本题的精彩!







