(43)2025年武汉市中考
江夏等四个区一模数学第24题
如图1,抛物线
y=a(x-1)²-4a
与x轴交于A, B两点,与y轴负半轴交于
点C , OC=3/2,
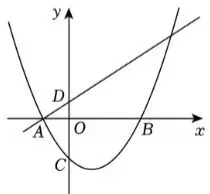
图1
(1)直接写出抛物线的解析式为_______,
(2)如图1,若D(0,1/2)为y轴上一点,
M是直线AD 上一点(不与D重合),点N
是抛物线上一点.若线段MN与CD恰好
关于平面内一点P成中心对称,求点P的
横坐标:
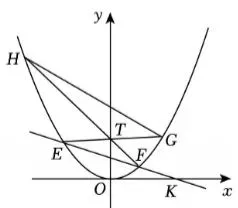
图2
(3)如图2,平移抛物线使其项点为
原点,过K(2,0)的直线交平移后的
抛物线于E, F两点,T(0,t)是y轴
正半轴上一点,直线ET交抛物线于
另一点G,直线FT交抛物线于另一
点H,设直线HG的解析式为
y=px+q,
试求t/p的值。
【解答】(1)由 OC=3/2,
可知C(0,-3/2),
把C(0,-3/2)代入到
y=a(x-1)²-4a
中,得
a-4a=-3/2,
解得 a =1/2
故抛物线的解析式为
y=1/2x²-x-3/2,
故答案为: y=1/2x²-x-3/2 .
(2)令y=0,得
1/2x²-x-3/2=0,
解得 x₁=-1,x₂=3,
故A(-1,0), B(3,0),
又∵D (0,2),由待定系数法可得
直线AD的表达式为 y=1/2x+1/2,
∵线段MN与CD恰好关于平面内一点P
成中心对称,
∴四边形DCMN为平行四边形, P点
为以DC和MN为对边的平行四边形的
对角线交点,
∴ MN⊥x 轴,
且 MN=CD=2,
故点P的横坐标为
xP=1/2xM,
∵M是直线AD上一点(不与D重合),
点N是抛物线上一点,
故设 M(m,1/2m+1/2),
N(m,1/2m²-m-3/2)
∴ MN=|1/2m+1/2-(1/2m²-m-3/2)|
=|-1/2m²+3/2m+2|
=2,
上式可分为两种情况:
①当﹣1/2m²+3/2m+2=2时,
解得 m₁=3,
m₂=0(舍去),
此时 xP=3/2,
当﹣1/2m²+3/2m+2=-2时,
解得 m=(3±√41)/2,
此时 xP=(3±√41)/4,
综上,点P的横坐标为
3/2或(3+√41)/4或(3-√41)/4,
(3)由题意可知,平移后的抛物线
表达式为
y=1/2x² ,
∵K (2,0),
设直线KE的表达式为
y=k(x-2),
联立直线KF与物线
y=1/2x² ,
整理可得
1/2x²-kx+2k=0,
由韦达定理可得
xE+xF=2k,
xE·xF=4k,
又∵T(0,t),
故设直线ET表达式为
y=mx+t,
设直线FT的表达式为
y=nx+t,
联立直线ET与抛物线
y=1/2x²,
整理可得
1/2x²-mx-t=0
由韦达定理可得
xE·XG =-2t,
∴ xG=-2t/xE ,
联立直线FT与抛物线
y=1/2x²,
同理可得
xH=﹣2t/xF ,
联立直线HG与抛物线
y=1/2x²,
整理可得
1/2x²﹣px-q=0,
由韦达定理有
xH+xG=2p ,
即 ﹣2t/xF+(-2t/xE)=2p,
∴ ﹣2t(xF+xE)/(xF·xE)=2p,
∴ -2t(2k)/4k=2p,
∴ t=-2p,
整理可得 t/p=-2.
往期文章







