(40)2025年重庆市中考
渝北区一模数学第26题
在等边三角形ABC中,线段CA绕点C
顺时针旋转α度至CD(0<α<180°),
连接BD, AD,交CA于点G .
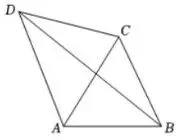
图1
(1)如图1,当旋转角α为75°时,
已知AB=√5,求△BCD的面积,
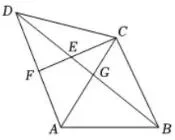
图2
(2)如图2,点F是线段AD上一点,
连接CF与BD相交于点E,
若∠CEB=60°.猜想线段EB,EC,EF
之间的数关系,并证明你的猜想,
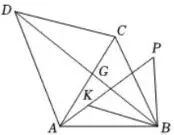
图3
(3)如图3,在⑴的条件下,点P为平面内,所在直线上方一动点,
满足∠APB=60°,点K为射线AP上一点,
使得BP=2AK,请直接写出BK的最小值.【解析】(1)如图4,作BE⊥CD ,
交DC的延长线于E ,
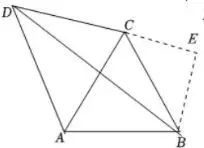
图4
∴∠E=90°,
∵△ABC是等边三角形,
∴∠ACB=60°,
AC=BC=AB=√5 ,
∵线段CA绕点C顺时针旋转75°至CD ,
∴ CD=BC=√5,
∠ACD=75°,
∴∠BCE=180°-∠ACB-∠ACD
=45°,
∴BE=√2/2BC=√10/2,
∴ S△BCD=1/2CD·BE
=1/2x√5x√10/2
=5√2/4,
(2)如图5,连接 AE ,
在BE上截取EH=CE ,
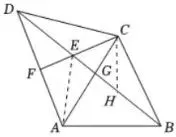
图5
∵∠CEB=60°,
∴△CEH是等边三角形,
∴∠CEH=60°,
CE=CH ,
∵△ABC是等边三角形,
∴∠ACB=∠BAC=60°,
AC=BC ,
∴∠CEB=∠BAC ,
∠ECH=∠ACB ,
∴点A,B,C,E共圆,
∠ACE=∠BCH ,
∴∠CBE=∠CAE ,
∠AEF=∠CAB=60°,
∴△BCH≌△ACE (ASA),
∴BH=AE ,
∠AEF=180°-∠CEB-∠AEB
=60°,
∵∠CDB=∠CBD ,
∠CED=∠CHB=120°,
CE = CH ,
∴△BCH≌△DCE ( SAS )
∴△ACE≌△DCE ,
∴∠ACE=∠DCE ,
∴ CF⊥AD ,
∴BH=AE=2EF,
∴EB=EH+BH=CE+2EF,
(3)如图6,作∠BAQ=120°,
截取AQ=1/2AB=√5/2,连接KQ ,
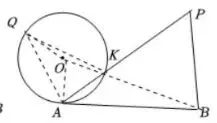
∵∠ABP+∠PAB=180°-∠APB
=120°,
∴∠QAK=∠ABP ,
∵AQ/AB=AK/BP=1/2,
∴△AKQ∽△BPA ,
∴∠AKQ=∠APB=60°,
作等腰△AOQ ,
使 OA=OQ,
∠AQO=∠OAQ=30°,
∴∠AOQ=120°,
∴点K在以O为圆心,
OA为半径的圆上,
连接OB ,交⊙O于K ,
当点K在K处时,BK最小,
∵∠BAO=∠BAQ-∠QAO
=120°-30°
=90°,
AB=√5,
OK=OA=AQ/(2sin∠AKQ)
=(√5/2)/(2x√3/2)
=√15/6,
∴OB =√[(√5)²+(√15/6)²]
=√165/6
∴BK最小=OB-OK
=(√195-√15)/6 .
往期文章






