命题趋势||2026年成都中考数学命题趋势分析与近期备考策略

中考数学

2026年成都中考数学命题将确立“素养立意”与“分层选拔”的双重基调。试卷结构预计将保持A卷（100分）与B卷（50分）的双卷制，但在题量分布上将进行微调：基础题占比将从2025年的75%微降至55%左右，以保障普高线学生的合格率；而压轴题占比虽降至15%，但跨模块融合度将显著提升，重点考查函数与几何的深度结合及高阶思维。命题趋势呈现出“去套路化”的显著特征，强调数学建模、逻辑推理与运算能力，跨学科（特别是物理）融合与本土化情境将成为新常态。备考策略需从机械刷题转向回归教材、强化情境转化与规范表达。

老吴Woo

  命题导向分析

  在“双减”政策深入实施与新课程标准全面落地的宏观背景下，2026年成都中考数学命题面临着深刻的变革。教育部及四川省教育厅明确指出，考试评价体系需从“知识立意”向“素养立意”转型，旨在通过考试引导教学回归育人本质，减少死记硬背和机械刷题。

   根据成都市教育局及相关部门的政策导向，2026年中考将继续坚持“稳中求进”的总基调。一方面，为了适应“指标到校”比例的扩大及普职分流的优化，命题需兼顾初中毕业生的学业水平评价与高中的选拔功能；另一方面，试卷必须严格依据义务教育课程标准，不超标命题，减少记忆性试题，增加情境化、综合性试题的比重 。

   特别值得注意的是，随着2025年成都中考取消“省重线”，仅保留“普高线”和“职普融通线”，2026年的命题在难度把控上将更加注重基础题的覆盖面与梯度设计，既要让绝大多数学生能够通过考核升入高中，又要为优质高中的选拔提供足够的区分度 。此外，教育部关于“减少超纲超标、死记硬背和‘机械式刷题’”的要求，直接导致了命题形式的创新，如概念开放题的出现，以及对通性通法考查的强化 。

 试卷结构演变与分值分布预测

一、试卷形式与题型结构

  2026年成都中考数学试卷将继续沿用A卷（基础卷）与B卷（提高卷）的两卷制模式，总分150分，考试时间120分钟。这种结构旨在通过A卷考查学生的数学素养与基本技能，通过B卷考查学生的综合运用能力与高阶思维 。

表格说明：

  从上表可以看出，试卷的整体架构保持了极高的稳定性，题量稳定在26道。2026年的主要变化在于题型的微调，特别是预测将新增“概念开放题”，这标志着命题从单一的解题转向了对数学概念本质的理解与再创造 。此外，B卷作为选拔人才的关键阵地，其解答题的压轴地位不可动摇。

【2025年成都市中考数学试题及参考答案】

二、难度系数与分值分布预测

  基于2025年试卷“基础题占比75%”的数据，结合2026年政策对“基础扎实性”的强调，预计2026年基础题的占比将维持高位，但压轴题的内部结构将发生质的变化。

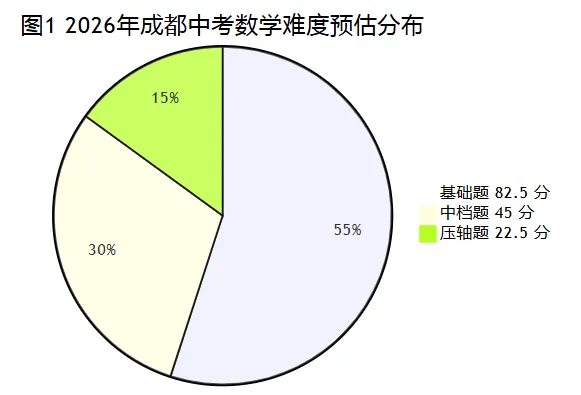
图表解读：

   如图1所示，2026年预估基础题分值为82.5分(占比55%)，较2025年的75%略有回调，这符合“提质增效”的要求，确保试卷的及格率与区分度之间的平衡。中档题保持30%(45分)的稳定比例，主要集中在知识点的灵活应用与转化上。压轴题占比下降至15%(22.5分)，但这并不意味着难度降低，而是意味着这15%的题目将承载更高的思维密度与跨学科融合度，成为顶尖学生决胜的关键 。

核心考点与命题逻辑演变

一、 函数板块：核心地位的持续强化

  函数是初中数学的“主干知识”，也是连接代数与几何的桥梁。数据显示，函数综合题的分值占比已从2023年的25%攀升至2025年的30%，确立了其在试卷中的核心地位 。【四川各地中考真题二次函数专项】

二次函数压轴化：B卷第26题通常为二次函数综合题，考查形式从单一的图像性质转向了“几何+代数”的深度捆绑。例如，结合抛物线的定点问题、定值问题，以及与一次函数、反比例函数的交点问题 。

代数思维的渗透：2026年的趋势显示，几何问题的解决将更加依赖代数工具。例如，利用坐标系将几何图形“量化”，通过设未知数、列方程（组）、解方程来解决几何中的长度、角度或面积问题。这种“代几融合”的考查方式，要求学生具备极强的代数运算能力 。

二、几何板块：从“模型套路”回归“逻辑本质”

  近年来，成都中考几何题呈现出明显的“去模型化”趋势。繁琐的辅助线模型(如“阿氏圆”、“手拉手”等)虽然并未完全消失，但其考查频率明显下降，取而代之的是对基础几何性质的深度挖掘与逻辑推理的完整性。

  圆与相似的权重提升：统计数据显示，圆与相似三角形的分值占比从2023年的12%上升至2025年的18%，增长幅度显著 。

  静态几何与基础模型：2025年及未来的命题将更加侧重于静态几何的证明，如“切线与弧中点+相似证明”、“A型/X型相似”的转换。这意味着学生必须熟练掌握基本图形的性质，而非死记硬背复杂的模型结论 。

   逻辑推理的严密性：试题开始引入高中逻辑用语（如全称量词、存在量词），并要求证明过程严谨规范。例如，在几何证明题中，不仅要求写出结论，更要求写出依据（定理、公理），这对学生的逻辑表达能力提出了更高要求。

三、统计与概率：从“计算”走向“决策”

   统计与概率板块的考查重心正在发生转移，即从单纯的数据计算转向基于数据的分析与决策。

   数据解读能力：试题不再要求机械地计算平均数或方差，而是要求学生能够读懂统计图表（如频数分布直方图、扇形图），理解数据背后的信息，并根据数据特征进行合理的预测或决策 。

  跨平台比较：结合社会热点（如快递服务、学生体质监测），要求学生利用统计知识对不同方案或不同群体进行比较分析，体现了数学在现实生活中的应用价值 。

四、 创新题型与情境化命题分析

1、跨学科融合：物理与数学的深度交汇

   跨学科融合是近年来成都中考命题的一大亮点，也是2026年的重点趋势之一。数学与物理的结合尤为紧密，主要体现在利用物理背景构建数学模型。

   典型情境：利用欧姆定律、焦耳定律或运动学公式构建反比例函数或一次函数模型 。

   考查逻辑：试题往往给出一个物理变化过程（如电压不变时电流与电阻的关系），要求学生剥离物理背景，提取出数学关系式，进而解决最值、范围或判断函数图象的问题。这种题型不仅考查数学能力，更考查学生提取信息、建立模型的综合素养 。

2、 本土化与传统文化：数学文化的落地

  试题中融入了大量成都本土元素和中华优秀传统文化，这些题目往往“形散而神不散”，即背景新奇，但考查的核心数学知识却是课本中的基础内容。

  本土元素：如以“成都大运会”、“世园会”、“蜀宝文创定价”为背景的应用题，或者结合“土圭测日影”考查相似三角形测高的题目 。

  传统文化：引用《九章算术》中的“盈不足”问题或“埃及分数”拆分，考查方程思想或规律探究。这类题目要求学生具备较强的阅读理解能力，能够将古文或复杂的文字描述转化为数学语言。

3、开放性与探究性试题

  为了打破“唯分数论”，试卷中增加了开放性试题的比重。这类题目往往没有唯一的答案，或者结论需要学生自行探索。

  类型：包括条件开放、结论开放、策略开放等。

  案例：如“是否存在实数k，使得某几何图形满足特定性质”，或者“请补充一个条件，使得三角形全等”。这类题目鼓励学生发散思维，敢于质疑，体现了“素养立意”的导向 。

 2026年备考策略与建议

一、分层教学与备考策略

  针对不同层次的学生，备考策略应有所侧重，以实现效益最大化。

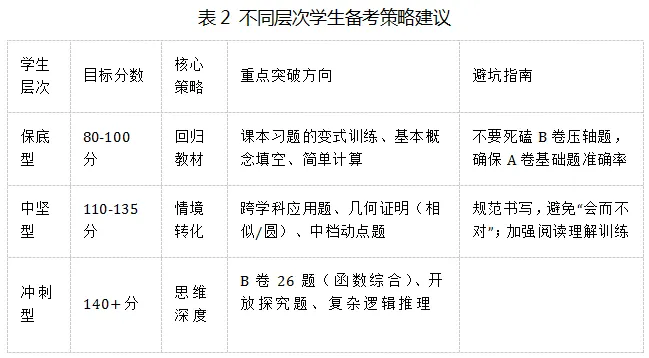
表格说明：

  对于保底型学生，核心任务是“拿基础分”，重点攻克A卷前10题和B卷前3题；对于中坚型学生，关键在于提升中档题的解题速度与准确率，特别是应用题和几何证明；对于冲刺型学生，则需要进行高阶思维训练，适应“去模型化”的趋势，重点突破B卷压轴题 。

二、针对性训练建议

1、回归教材，深挖例题：

   由于近60%的基础题改编自教材，学生应重新梳理教材中的典型例题，进行条件的增减、结论的变式训练。例如，将教材中的证明题改为探索题，或将特殊图形改为一般图形，以培养知识的迁移能力 。

2、强化运算，规范书写：

  鉴于几何题中代数化的趋势，学生必须强化代数运算能力，特别是含参方程、分式化简及复杂的解直角三角形运算。同时，在平时训练中必须养成规范书写习惯，逻辑推理要严密，步骤要完整，避免因“跳步”而失分 。

3、关注热点，拓宽视野：

  适度引入全国各省市（如浙江、江苏、北京）的优质试题，特别是那些涉及跨学科融合、开放性设问的题目，以拓宽解题视野。同时，关注科技前沿（如人工智能、脑机接口）和传统文化，培养从复杂情境中提取数学信息的能力 。

4、心理调适与应试技巧：

  面对“概念开放题”等新题型，学生容易产生畏难情绪。备考中应进行专门的心理调适，建立“陌生题不丢分”的信心。在考试中，应遵循“先易后难”的原则，合理分配时间，切忌在某一道题上“死磕”太久，确保基础分“颗粒归仓” 。

   总之，对于广大考生而言，单纯依赖题海战术和套路化解题的路径已行不通。唯有回归教材本质，夯实基础知识，强化运算能力，提升情境转化素养，才能在未来的中考中立于不败之地。

初中数学精品资料

更新中.........