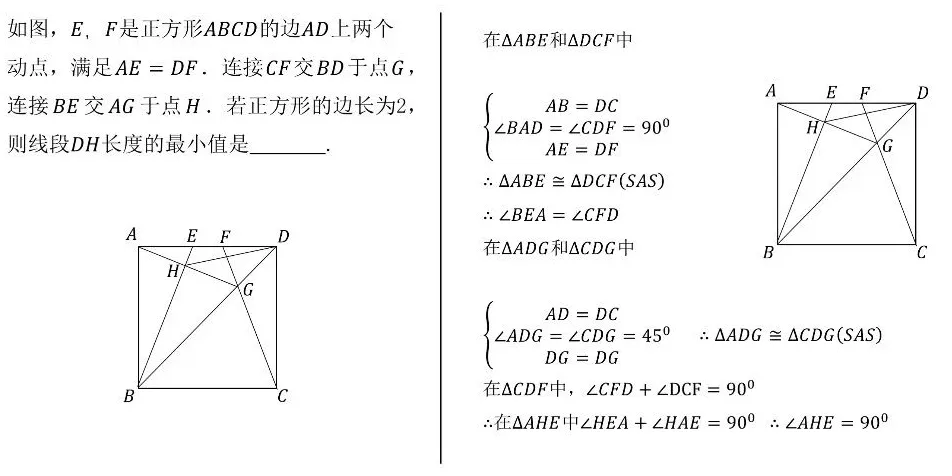
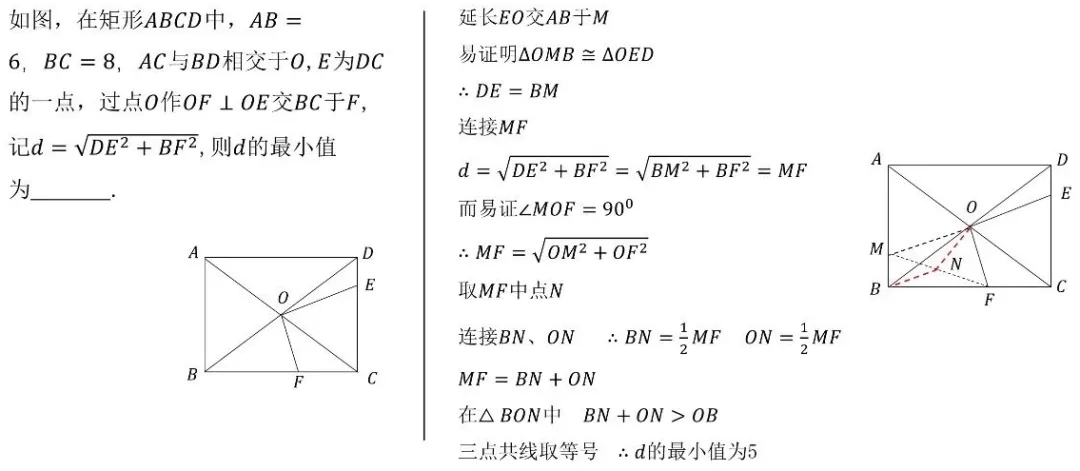
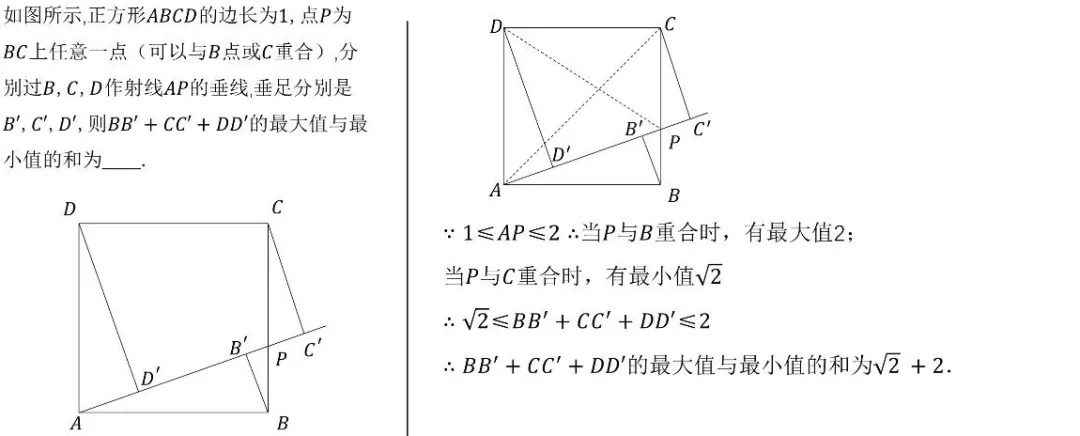
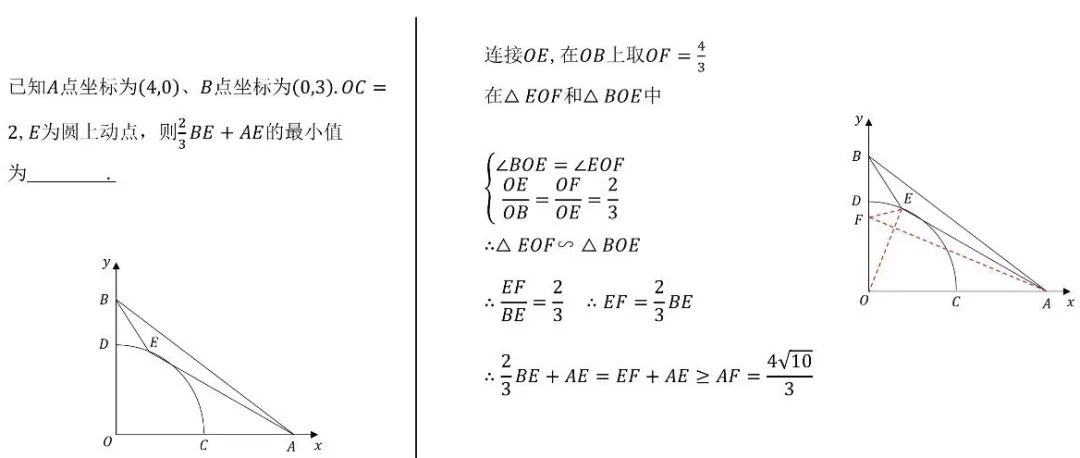
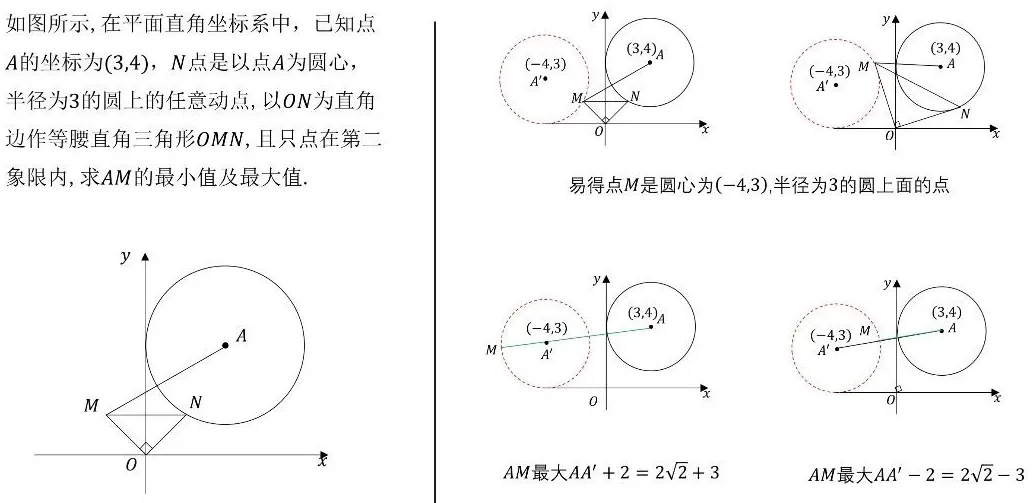
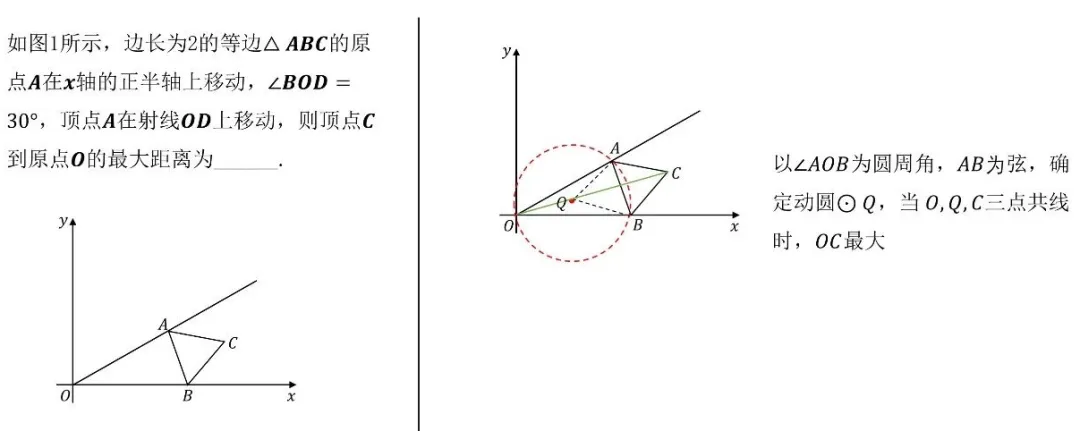
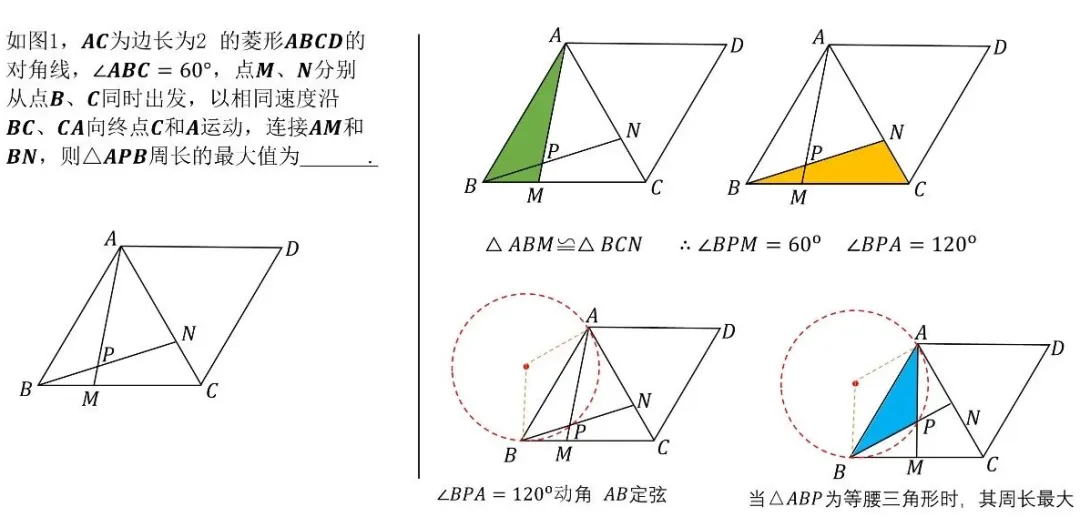
在中考数学的战场上,动点最值问题一直是令无数考生头疼的"拦路虎"。这类题目不仅考察几何直观,更考验代数运算与逻辑推理的综合能力。今天,我们为大家系统梳理19大经典动点最值模型,帮你彻底攻克这一压轴难题!
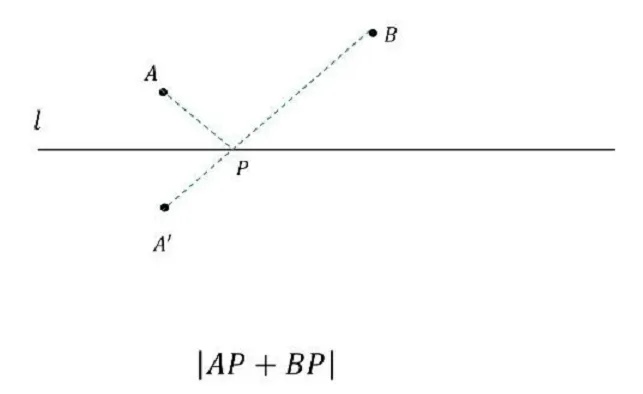
一、将军饮马模型:对称变换的妙用
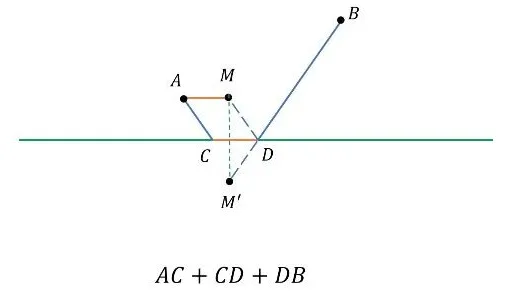
"将军饮马"是最经典的最值问题模型。其核心思想是:利用对称变换将折线转化为直线,从而应用"两点之间线段最短"的基本原理。
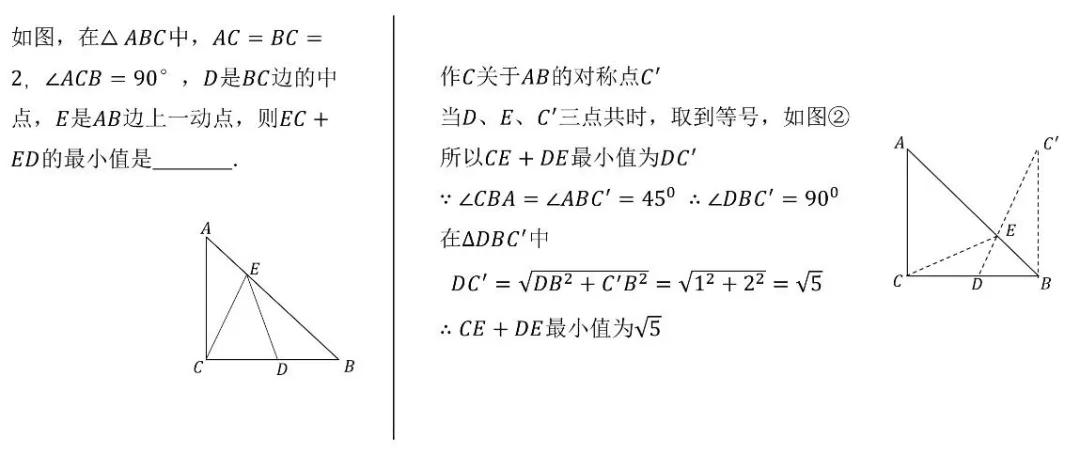
例如,在等腰直角三角形ABC中(AC=BC=2,∠ACB=90°),D为BC中点,E在AB边上运动,求EC+ED的最小值。通过作C关于AB的对称点C',当D、E、C'三点共线时,EC+ED取得最小值√5。这一模型告诉我们:遇到"和最小"问题,首先考虑对称变换。
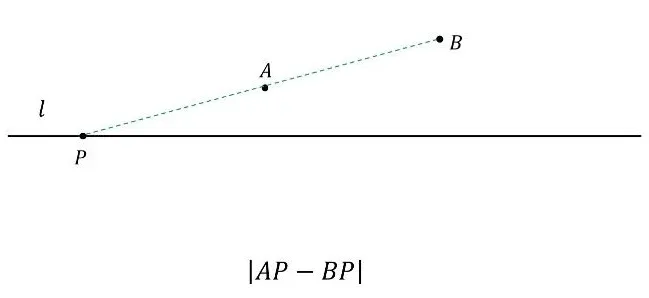
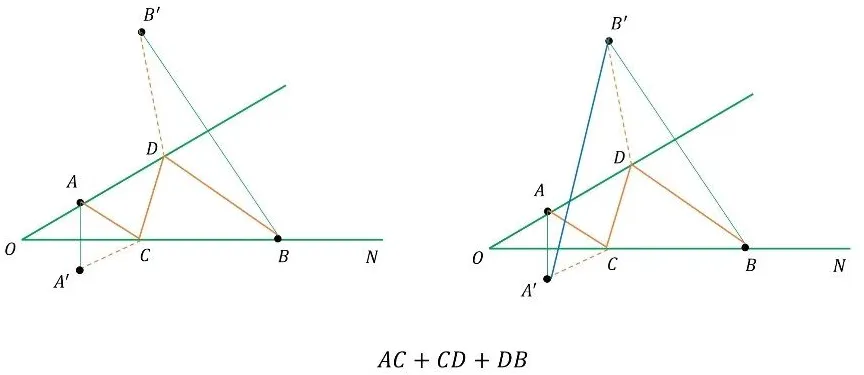
二、差最大模型:三角形两边之差的智慧
与"和最小"相对应的是"差最大"问题。这类问题通常利用三角形两边之差小于第三边的性质,通过构造对称点,将问题转化为三点共线的情形。
比如,已知A(1,5)、B(3,-1),M在x轴上运动,求AM-BM的最大值。通过作B关于x轴的对称点B'(3,1),连接AB'并延长交x轴于M(7/2,0),此时AM-BM取得最大值。记住口诀:求差最大,对称后连线延长。
三、其他核心模型速览
除了这两大基础模型,动点最值问题还包括:
垂线段最短模型:点到直线的距离,垂线段最短
旋转最值模型:利用旋转构造全等或相似三角形
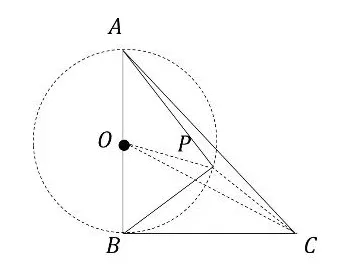
圆外一点到圆上点距离的最值:连心线延长线与圆的交点
阿氏圆模型:到两定点距离之比为定值的点的轨迹
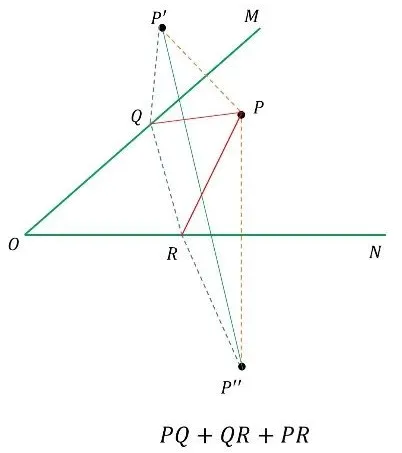
费马点模型:到三角形三顶点距离之和最小的点
胡不归模型:带权重的路径最短问题
瓜豆原理:主从联动,轨迹相似
四、解题策略总结
面对动点最值问题,建议按以下步骤思考:
识别模型:判断属于"和最小"、"差最大"还是其他类型
构造转化:通过对称、旋转、平移等变换,将动点问题转化为定点问题
建立函数:必要时用代数方法,建立目标函数求最值
验证取值:检查等号成立条件是否在允许范围内
五、备考建议
动点最值问题虽然变化多端,但万变不离其宗。建议同学们:
熟练掌握19大基本模型的图形特征和解题套路
建立错题本,归纳同类问题的通性通法
注重一题多解,培养几何直观与代数运算的双重能力
限时训练,提高压轴题的解题速度和准确率
中考数学的压轴题并非不可逾越的高山。只要掌握这19大动点最值模型,理解其背后的数学思想,你就能在考场上从容应对,将"送命题"变成"送分题"!