【中考数学】相交线与平行线动点问题

一、如图，已知AB∥CD，C在D的右侧，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E．∠ADC=70°.

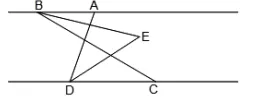
（1）求∠EDC的度数；解：∵DE平分∠ADC，∠ADC=70°，∴∠EDC=1/2∠ADC=1/2×70°=35°；

（2）若∠ABC=n°，求∠BED的度数（用含n的代数式表示）；

解：过点E作EF∥AB，（关注微信公众号：初一数学语文英语）

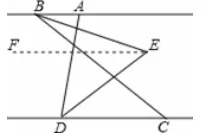
∵AB∥CD，∴AB∥CD∥EF，∴∠ABE=∠BEF，∠CDE=∠DEF，

∵BE平分∠ABC，DE平分∠ADC，

∠ABC=n°，∠ADC=70°，∴∠ABE=1/2∠ABC=1/2n°，

∠CDE=1/2∠ADC=35°，（关注微信公众号：初一数学语文英语）∴∠BED=∠BEF+∠DEF=1/2n°+35°；

（3）将线段BC沿DC方向平移， 使得点B在点A的右侧，其他条件不变，若∠ABC=n°，（关注微信公众号：初一数学语文英语）求∠BED的度数（用含n的代数式表示）．

解：过点E作EF∥AB

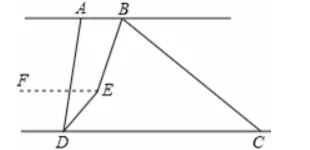
∵BE平分∠ABC，DE平分∠ADC，

∠ABC=n°，∠ADC=70°∴∠ABE=1/2∠ABC=1/2n°，

∠CDE=1/2∠ADC=35°（关注微信公众号：初一数学语文英语）

∵AB∥CD，∴AB∥CD∥EF，∴∠BEF=180°-∠ABE=180°-1/2n°，

∠CDE=∠DEF=35°，∴∠BED=∠BEF+∠DEF=180°-1/2n°+35°

=215°-1/2n°.

二、在平面直角坐标系中，点A,B分别是x轴，y轴上的点，且OA=a，OB=b，其中a,b满足∨(a+b-32)+|b-a+16|=0，将B向左平移18个单位得到点C。

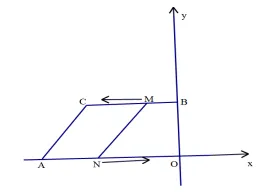
（1）求点A,B,C的坐标；

解：由题意得a+b-32=0,b-a+16=0;

解a=24,b=8,

∴A(-24,0),B(0,8),C(-18,8)

（2）点M,N分别为线段BC，OA上的两个动点，点M从点B以1个单位/秒的速度向左运动，同时点N从点A以2个单位/秒的速度向右运动，设运动时间为t秒（0≤t≤12）.当BM=ON时，求t的值。

解：由题意得，BM=t，AN=2t，OA=24,

∴ON=24-2t；

∵BM=ON，∴t=24-2t;得t=3

三、如图，以直角三角形AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0， a），C（b，0）满足∨(a-2b)+|b-2|=0.

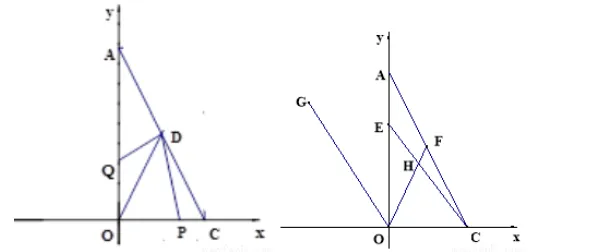（1）则C点的坐标为 (2，0) ;A点的坐标为 (0,4) ．

（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，（关注微信公众号：初一数学语文英语）Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．AC的中点D的坐标是（1,2），设运动时间为t（t＞0）秒．问：是否存在这样的t，使S△ODP=S△ODG,若存在，请求出t的值；若不存在，请说明理由．

解：由题意可得：OP=2-t，QO=2t，D（1，2），则S△DOP=1212OP•yD=1212（2-t）×2=2-t，S△DOQ=1212OQ•xD=1212×2t×1=t，∵S△ODP=S△ODQ，∴2-t=t，∴解得：t=1，

（3）点F是线段AC上一点，满足∠FOC=∠FCO, 点G是第二象限中一点，连OG,使得∠AOG=∠AOF．点E是线段OA上一动点，连CE交OF于点H， 当点E在线段OA上运动的过程中（关注微信公众号：初一数学语文英语）∠OHC+∠ACE=∠OEC，的值是否会发生变化,若不变，请求出它的值；若变化，请说明理由．

解：∠OHC+∠ACE/∠OEC的值不变，其值是2∵∠2+∠3=90°，又∵∠1=∠2，∠3=∠FCO，∴∠GOC+∠ACO=180°，∴OG∥AC，∴∠1=∠CAO，∴∠OEC=∠CAO+∠4=∠1+∠4，

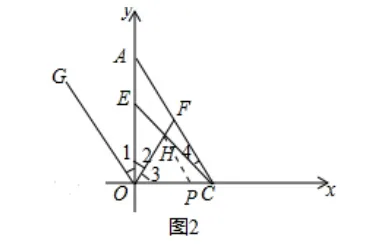
如图，过H点作AC的平行线，交x轴于P，

则∠4=∠PHC，PH∥OG，∴∠PHO=∠GOF=∠1+∠2，∴∠OHC=∠OHP+∠PHC=∠GOF+∠4

=∠1+∠2+∠4，

∠OHC+∠ACE/∠OEC=2．

👉中考数学经典考点专题复习微课

👉小学全科目知识梳理汇总

👉小学数学每日一练习题120篇

👉小学作文看图写话汇总