天津中考数学第24题是几何变换综合题,固定位于试卷中档压轴位置,分值10分,是区分度较高的核心题目之一。该题以平面直角坐标系为载体,聚焦图形变换(平移、折叠/翻折、旋转),结合特殊图形性质,通过三问递进式设计,全面考查学生的几何直观、逻辑推理与数学建模能力。
1.基本定位与分值结构
固定位置:第24题,几何压轴题,分类讨论,运算量较大
总分值:10分,通常分配为3分+4分+3分,梯度明显
命题周期:近6年呈现"平移与折叠交替"规律,单数年多考平移,偶数年多考折叠,旋转在2018年前较常见,近年偶有涉及。
2.核心图形背景
必含坐标系:所有题目均在平面直角坐标系中展开,强调坐标与几何的结合
特殊图形为主:
特殊三角形:直角三角形、等腰三角形、等边三角形(含30°/45°特殊角)
特殊四边形:矩形、正方形、菱形(近年以矩形为主)
简单组合图形:由特殊图形拼接而成,便于计算与变换
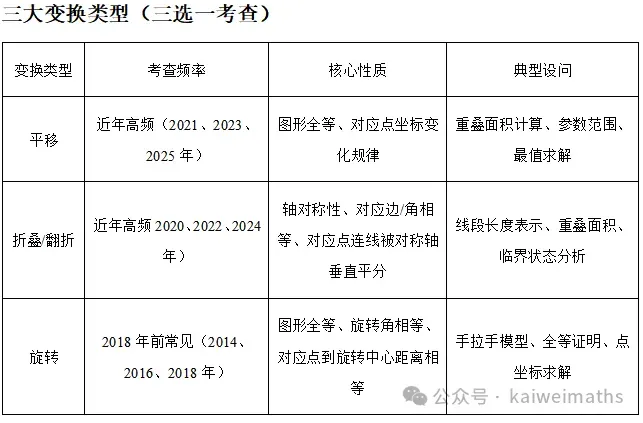
1.核心知识考点
图形变换性质:平移、折叠、旋转的定义与性质(全等性、对称性)
特殊图形性质:直角三角形(勾股定理)、等腰/等边三角形(三线合一)、矩形(对边相等、四角为直角)
坐标系应用:坐标计算、距离公式、函数思想(面积与参数的函数关系)
几何计算:线段长度、角度、面积(尤其重叠面积)的精准计算
2.核心思想方法
分类讨论:图形变换过程中不同位置状态的区分(如重叠部分形状变化)
数形结合:坐标系中几何问题的代数化表示与求解
临界分析:确定图形变换的起点、终点及特殊位置,界定参数范围
函数建模:将几何量(面积)表示为参数t的函数,进而求最值
空间想象:动态图形变化过程的可视化与逻辑推理
3.设问方式与考查层次(三问递进)
该题严格遵循"基础→综合→拓展"的梯度设计,体现由特殊到一般的思维过程:
第(Ⅰ)问:基础送分题(3分)
核心考查:图形变换基本性质、特殊图形性质、坐标计算
常见形式:求点坐标、线段长度、角度大小,或简单证明(如三角形全等)
难度系数:★★☆☆☆,多数学生可轻松得分,强调基础知识掌握
第(Ⅱ)问:综合应用题(4分)
核心考查:含参数(通常为t)的数学建模、重叠面积表示、分类讨论思想
常见形式:
用含t的代数式表示重叠部分面积/线段长度
确定参数t的取值范围(关键在于找到图形变换的临界状态)
结合全等/相似三角形进行多步推理
难度系数:★★★★☆,区分中等与良好学生,要求较强的空间想象与计算能力
第(Ⅲ)问:拓展探究题(3分)
核心考查:参数范围下的最值问题、图形动态分析、高阶思维能力
常见形式:
求重叠面积的最大值/最小值或取值范围
探究特殊位置下的图形性质或参数值
难度系数:★★★★★,区分良好与优秀学生,强调临界分析与逻辑严谨性
1.课程安排(课程视频可以反复观看)
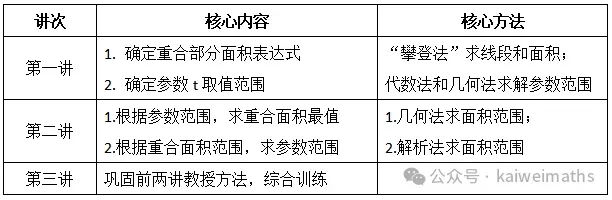
2.时间规划
线上线下同步开课,每周一期,随到随学。
3.配套训练
折叠变换、平移变换、旋转变换匹配5道课后训练,题目解题视频,试题答案。
4.答疑解惑
(1)针对24题突破课程,专项2小时线上免费答疑;
(2)课后配套训练试题答疑;
(3)中考前随时随地负责答疑,不限课程内容。
5.赠送《天津中考压轴题突破讲义》、《天津中考基础知识点手册》、《中考真题汇编》、《五年中考三年模拟试卷及答案》
课程详情,请加微信

获取更多小卷备考资料或试卷:
可以加“2026年天津小卷考试备考”群,









