(32)2025年合肥市中考
多校联考一模数学第23题
如图1,在平面直角坐标系中,抛物线
y=ax²+bx+2
与x轴交于A(1,0),于y轴交于B点,
以A为直角顶点, AB为腰作等腰直角
△ABC ,恰好C点落在抛物线上。
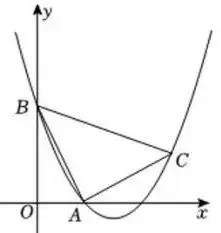
图1
【问题背景】
(1)直接写出点B坐标,并求抛物线的
函数表达式,
【初步探索】
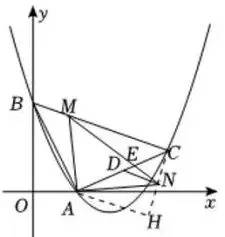
(2)如图2所示,点D为线段AC的中点,
点M为线段BC上一动点(点M不与点B,
C重合),连接AM,以A为旋转中心将
线段AM顺时针旋转90°得到线段AN,
连接DN,求DN的最小值:
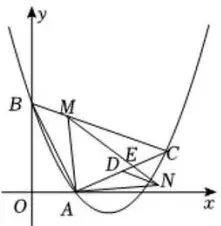
图2
【深度探究】
(3)如图2所示,连接MN交AC于点E,
在满足⑵最值的条件下,
求 S△MEC/S△AEN ,
【解析】(1)抛物线与x轴交于A(1,0)
与y轴交于B点,
令 x=0,
则 y=2,
∴ B (0,2),
以A(1,0)为直角顶点,AB为腰
作等腰直角三角形ABC ,
∴OA=1, OB=2,
∠BAC=90°,
∴ AB=√5=AC ,
如图3,过点C作CF⊥x轴于点F,
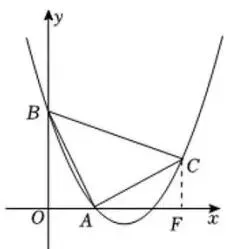
图3
∴∠BAO+∠CAF=∠CAF+∠ACF
=90°
∴∠BAO=∠ACF ,
又∵∠BOA=∠AFC=90°,
AB=CA ,
∴△BAO≌△ACF (AAS),
∴CF=OA=1,
AF=OB=2,
∴OF=OA+AF
=1+2
=3,
∴ C(3,1),
把A(1,0), C(3,1)代入抛物线
y=ax²+bx+2
中得 a+b+2=0,
9a+3b+2=1,
解得: a=5/6,
b=-17/6,
故抛物线的表达式为
y=5/6x²﹣17/6x +2,
(2)如图4,连接CN,过点D作DG⊥CN
于点G,
当点M在线段BC(不含端点)上运动时,
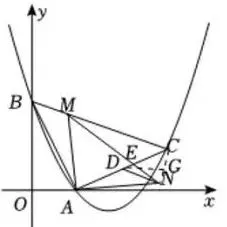
图4
当DG⊥CN,即点N与点G重合时,
DN的值最小,
∵△ABC 是等腰直角三角形,
AM绕点A顺时针旋转90°得到线段 AN,
∴ AB=AC ,
∠BAC=∠MAN=90°,
AM=AN ,
∠ABC=∠ACB=45°,
∴∠BAM=90°-∠MAC
=∠CAN ,
∴△BAM≌△CAN (SAS),
∴ BM=CN ,
∠ABM=∠ACN=45°,
∴∠ACB+∠ACB=45°+45°
=90°,
如图5,当点M在线段BC(不含端点)
上运动时,点N在CN上与运动,
当 DN⊥CN时,
DN的值最小,
∵AB=AC=√5,点D是AC中点,
∴DG=√2/2CD
=√2/2x√5/2
=√10/4,
故当点N于点G重合时,
DN的值最小,
最小值为DN=DG=√10/4,
(3)根据上述计算可得,
AB=BC=√5,
BC=√10,
由⑵可得,
△CDN是等腰直角三角形,
则 DN=CN=BM=√10,
∴ AH=CH=√10/2,
∴ MC=BC-BM
=√10-√10/4
=3√10/4,
如图6,过点E作EK⊥BC于点 K,
作ET⊥BC于点T ,
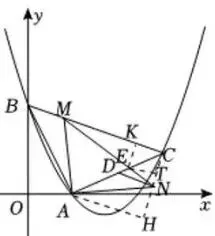
图6
由∠BCA=∠HCA=45°,
得四边形EKCT是正方形,
∵ DN⊥CH,BC⊥CH ,
∴DN//BC ,
∴△DEN∽△CEM ,
∴CE=3DE
且 DE+CE=CD=√5/2 ,
则 EK=ET=√2/2CE
=√2/2x3√5/8
=3√10/16 ,
则 S△CEN=1/2CN·ET
=1/2x√10/4x3√10/16
=15/64 ,
而 S△MCE=1/2MC·EK
=1/2x3√10/4x3√10/16
=45/64,
则 S△ACN=1/2CN·AH
=1/2x√10/4x√10/2
=5/8
则 S△AEN= S△ACN-S△CEN
=5/8-15/64
=25/64,
则 S△MEC/S△AEN=9/5 .
往期文章







