考点:二次函数含参问题
分级考点:二次函数增减性求参
【考点】
二次函数解析式;二次函数图象性质.
【来源】
选自中考冲刺教材《中考冲刺十招》第七招 比翼双飞看“数形”
【题干】
已知二次函数 ,其中 .
(1)若二次函数的图象经过 ,求二次函数表达式;
(2)若该二次函数图象开口向下,当 时,二次函数图象的最高点为,最低点为,点的纵坐标为,求点和点的坐标;
(3)在二次函数图象上任取两点,,
当时,总有,求的取值范围.
【解题技巧】
待定系数法求函数解析式;
二次函数图象特征;
二次函数图象性质;
数形结合、以形助数;
函数增减性在高中数学中的定义.
【解题思路】
(1)将点代入函数解析式:
化简得:,
解得:
因此,二次函数的表达式为
(2)对称轴:直线
∵ 图象开口向下,
∴
对称轴,如图所示:
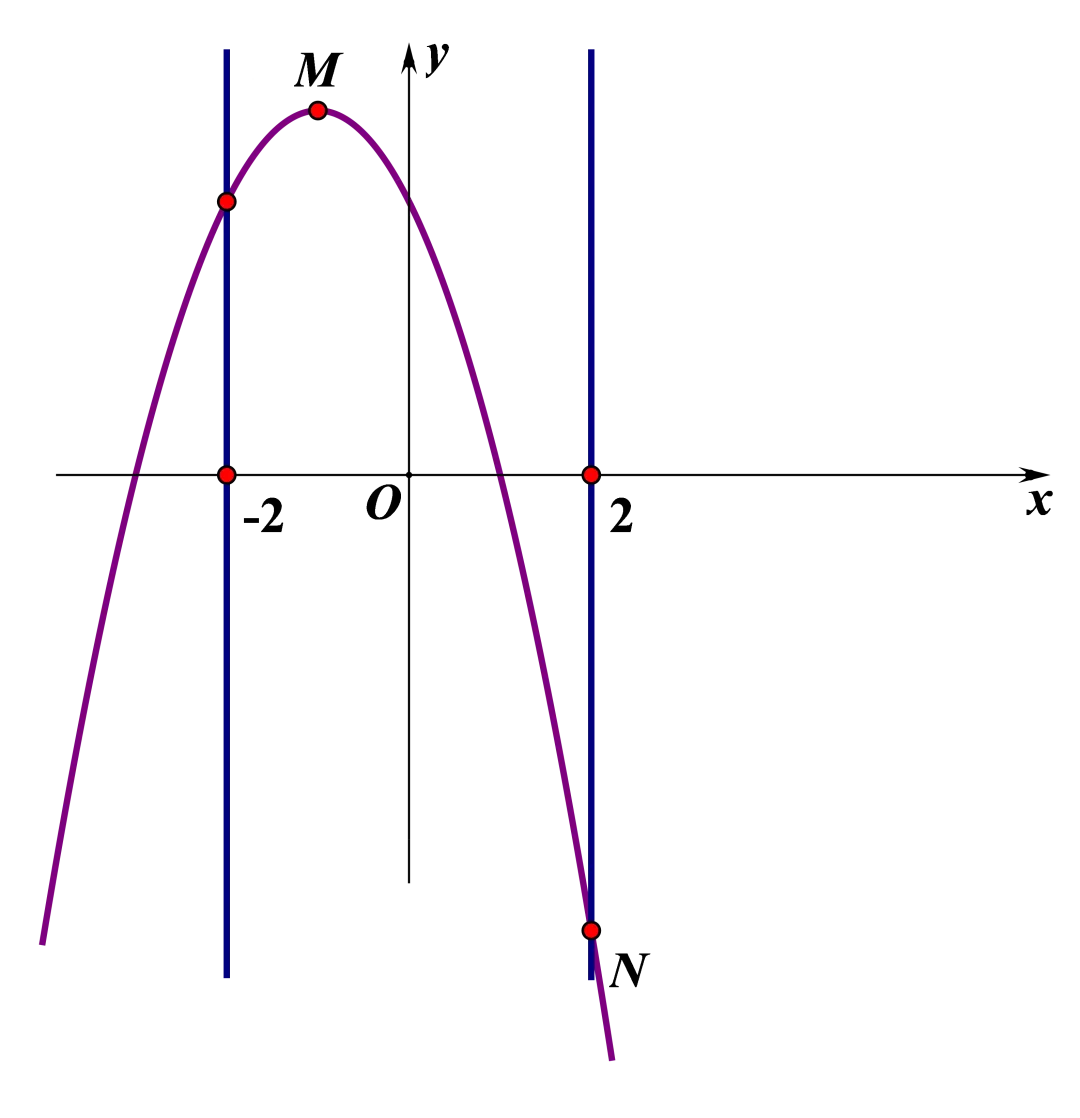
因此,顶点即为该区间内的最高点M,
即顶点坐标为
代入可得:,
解得:
此时,二次函数的表达式为,
,
开口向下,
在对称轴左侧随增大而增大,
右侧随增大而减小
当时,;
当时,
∵ ,
∴ 最低点N的坐标为
(3)由且可知,随的增大而减小
二次函数对称轴为直线,
① 时, 图象开口向上
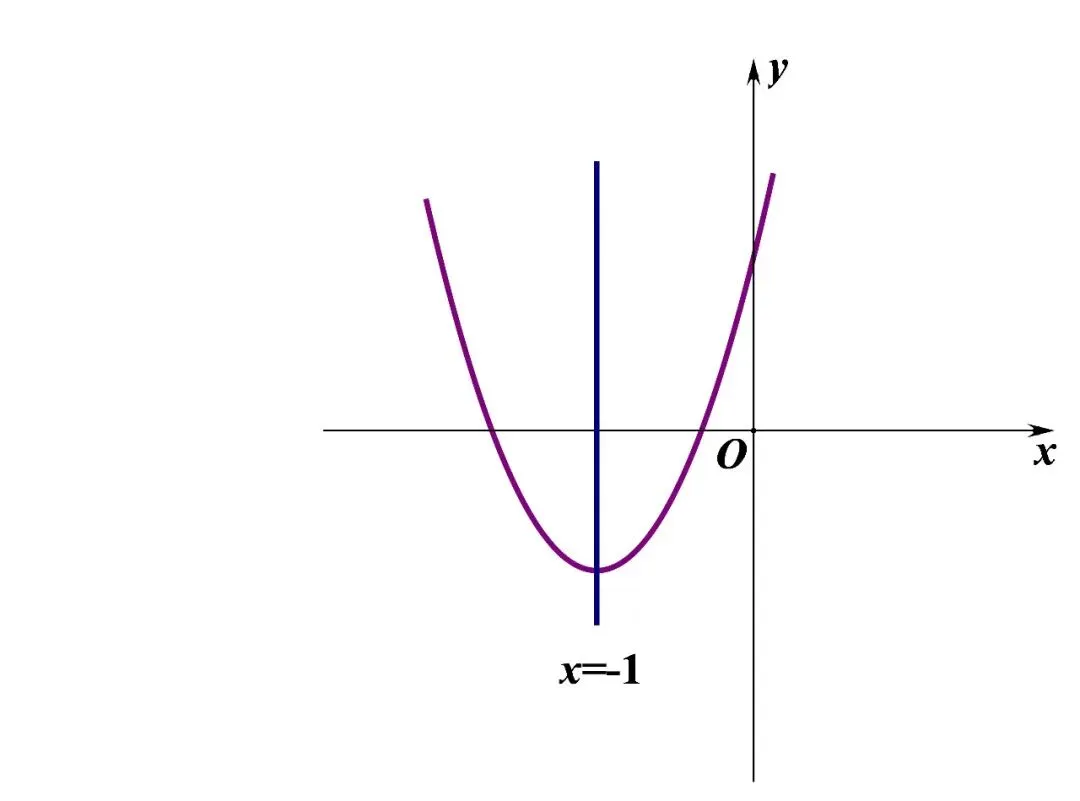
函数在对称轴左侧()随增大而减小
因此,
解得:
② 时,图象开口向下
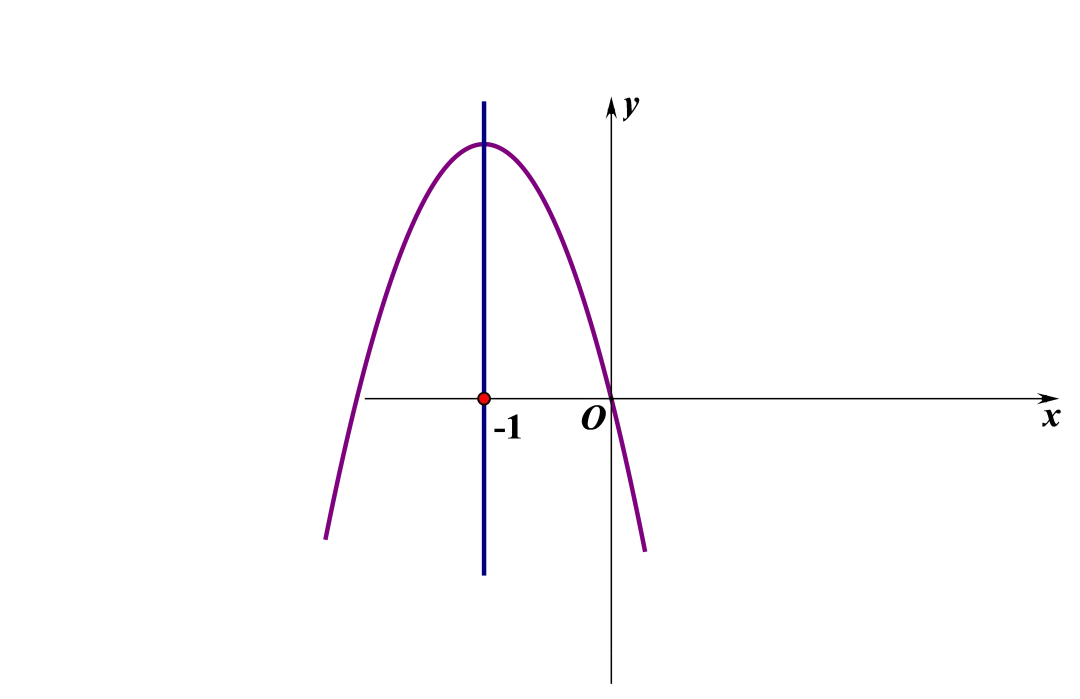
函数在对称轴右侧()随增大而减小,
因此,
综上,的取值范围为或
【延伸高中】
高中单调性的严格定义,我们先来看课本上的标准定义:
单调递增:一般地,设函数的定义域为,区间。 如果对区间内的任意两个数,都有, 那么就称函数在区间上单调递增,区间为的单调递增区间。 单调递减:同样地,设函数的定义域为,区间。 如果对区间内的任意两个数,都有, 那么就称函数在区间上单调递减,区间为的单调递减区间。
几个关键概念的理解
1.单调性是“局部性质”
一个函数可以在某些区间单调递增,在另一些区间单调递减,比如二次函数就是典型的例子。我们不能说“这个函数是增函数”,而要说“这个函数在哪个区间上是增函数”。
2.“任意”两个字很重要
定义里说的是“任意”,而不是“存在”某两个数。这是高中数学严谨性的体现,要证明一个函数单调,必须保证区间里的每一对数都满足条件。
3.常数函数没有严格单调性
如果一个函数的函数值永远不变,比如,那么对任意,都有,既不满足,也不满足,所以常数函数不具有严格的单调性。
举个例子
例如:一次函数
初中结论:, 随 增大而增大。
高中描述:函数在全体实数上单调递增。
验证定义:任取,则 所以,满足单调递增的定义。








