01

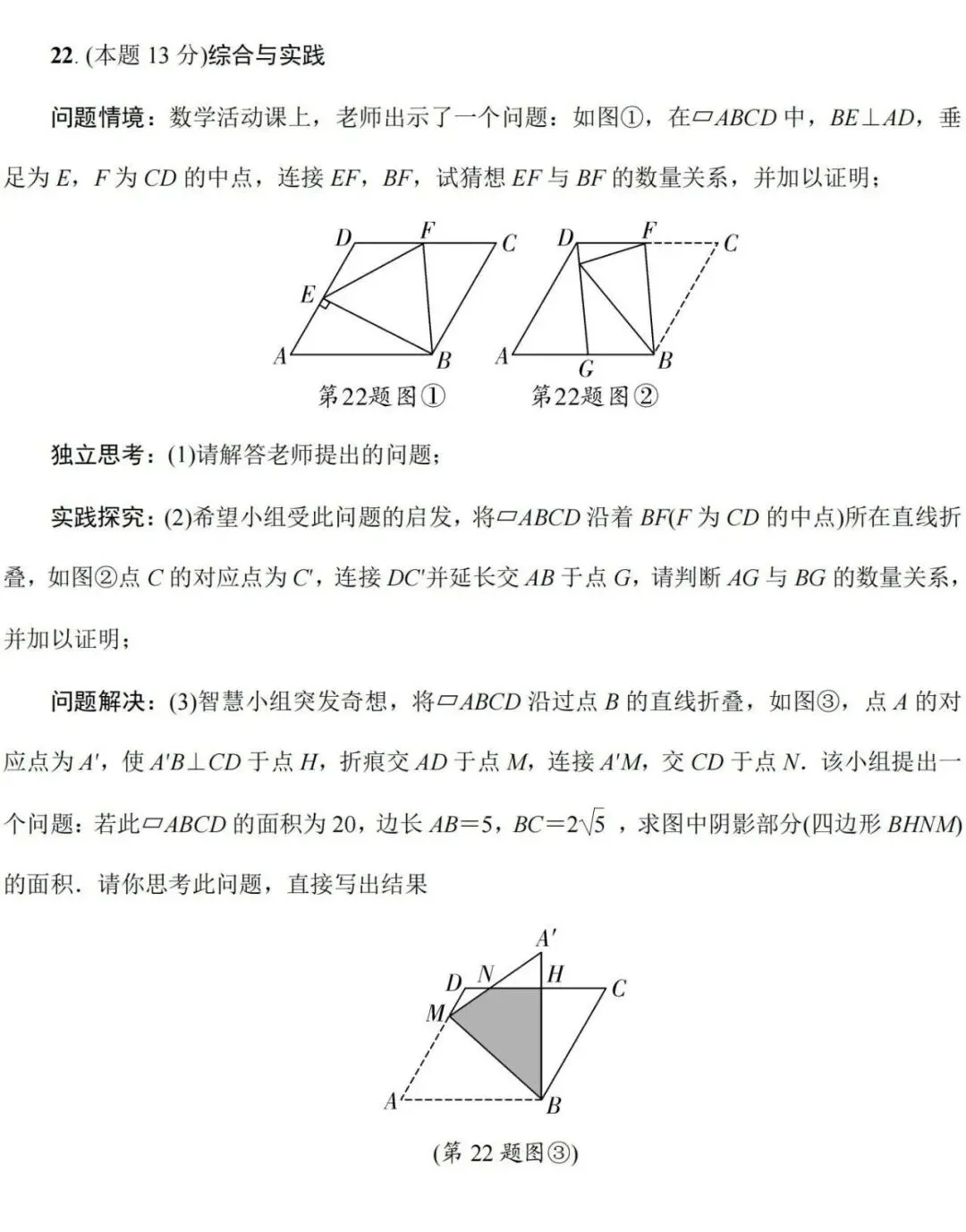
综合与实践
02
解析

二、各问解题思路与关键步骤
1.问题(1) EF与BF关系
猜想:EF=BF
关键证明方法:
中位线法:延长AD、BF交于M,通过全等△MDF≌△BCF证F为BM中点,结合直角三角形斜边中线定理。
垂直平分法:作FM⊥EB,利用平行线分线段成比例证EM=MB,得FM垂直平分EB。
易错点:忽略折叠对称性导致的全等关系,或误用中位线定理条件。
2.问题(2) AG与BG关系
结论:AG=BG
核心逻辑:
→FC'=FD→∠3=∠4→DG∥FB→平行四边形DGBF→BG=DF=½AB。
或通过CC'⊥FB证∠DC'C=90°→平行关系。
陷阱:未正确识别轴对称图形的对应角关系,导致平行证明失败。
3.问题(3) 阴影面积计算
关键步骤:
利用面积反推BH=4,勾股定理得CH=2。
相似三角形△A'ME∽△CBH建立比例关系,设ME=x解方程。
最终面积=△A'MB面积-△A'NH面积=22/3。
难点:折叠后角度关系复杂,需多次运用相似和勾股定理。
三、通用解题技巧
折叠问题口诀:"折痕是对称轴,对应边角全相等"
辅助线策略:中点问题常考虑倍长中线或构造中位线。
面积法:当线段关系复杂时,可尝试用面积比转化。
四、评分要点提醒
几何证明需严格写出"∵""∴"逻辑链,缺一步扣1分。
折叠问题未标注对应点直接扣2分。
相似三角形必须完整说明对应角相等、对应边成比例。






