中考常见几何模型大全!13种模型大全,覆盖16大高频考点

【中考常见几何模型大全！13种模型大全，覆盖16大高频考点】

一、全等三角形模型体系

1. 基础全等模型

（1）平移型全等：两个三角形通过平移变换完全重合，具有"边角边"的典型特征。如图形中的平行四边形的对角线分成的两个三角形，犹如镜像对称的双子星，完美诠释几何对称之美。

（2）轴对称全等：沿对称轴折叠后完全重合的图形，常见于等腰三角形、矩形等图形中。这类模型犹如蝴蝶展翅，在解题时往往需要构造对称辅助线。

2. 旋转全等模型

（1）共顶点旋转：两个三角形共享顶点，通过旋转一定角度实现全等。这种模型在正方形、等边三角形中尤为常见，解题时需要把握旋转角度与对应边的关系。

（2）中心对称全等：图形绕某点旋转180度后与原图形重合，如同昼夜交替般完美对应。平行四边形对角线分成的三角形就是典型例证。

二、相似三角形模型体系

1. A字型相似模型

由平行线切割形成的相似三角形，形如字母"A"。这种模型在梯形、普通三角形中都可能出现，解题时需注意对应边的比例关系，犹如阶梯般层层递进的比例推导。

2. 八字型相似模型

两条相交直线被平行线所截形成的相似三角形，状若数字"8"。这种模型在复杂图形中往往暗藏玄机，需要敏锐地发现隐藏的平行关系。

三、特殊四边形模型

1. 中点四边形模型

任意四边形各边中点连线必成平行四边形，犹如魔术般的神奇变换。当原四边形对角线垂直时，中点四边形升级为矩形；对角线相等时则变为菱形。

2. 梯形辅助线模型

（1）平移腰线法：将梯形一腰平移构造平行四边形，犹如搭建解题的桥梁。

（2）双高法：同时作两条高将梯形分割为矩形和两个直角三角形，这种分割方式好比精准的外科手术。

四、圆中的几何模型

1. 垂径定理模型

垂直于弦的直径平分弦及弦所对的两条弧，这个经典模型如同圆规画圆般精确完美。解题时常常需要构造直角三角形，利用勾股定理建立方程。

2. 切线长定理模型

从圆外一点引两条切线，切线长相等且夹角被连接线平分。这个优美的对称模型在解题时往往能化繁为简，犹如解开缠绕的线团。

五、动态几何模型

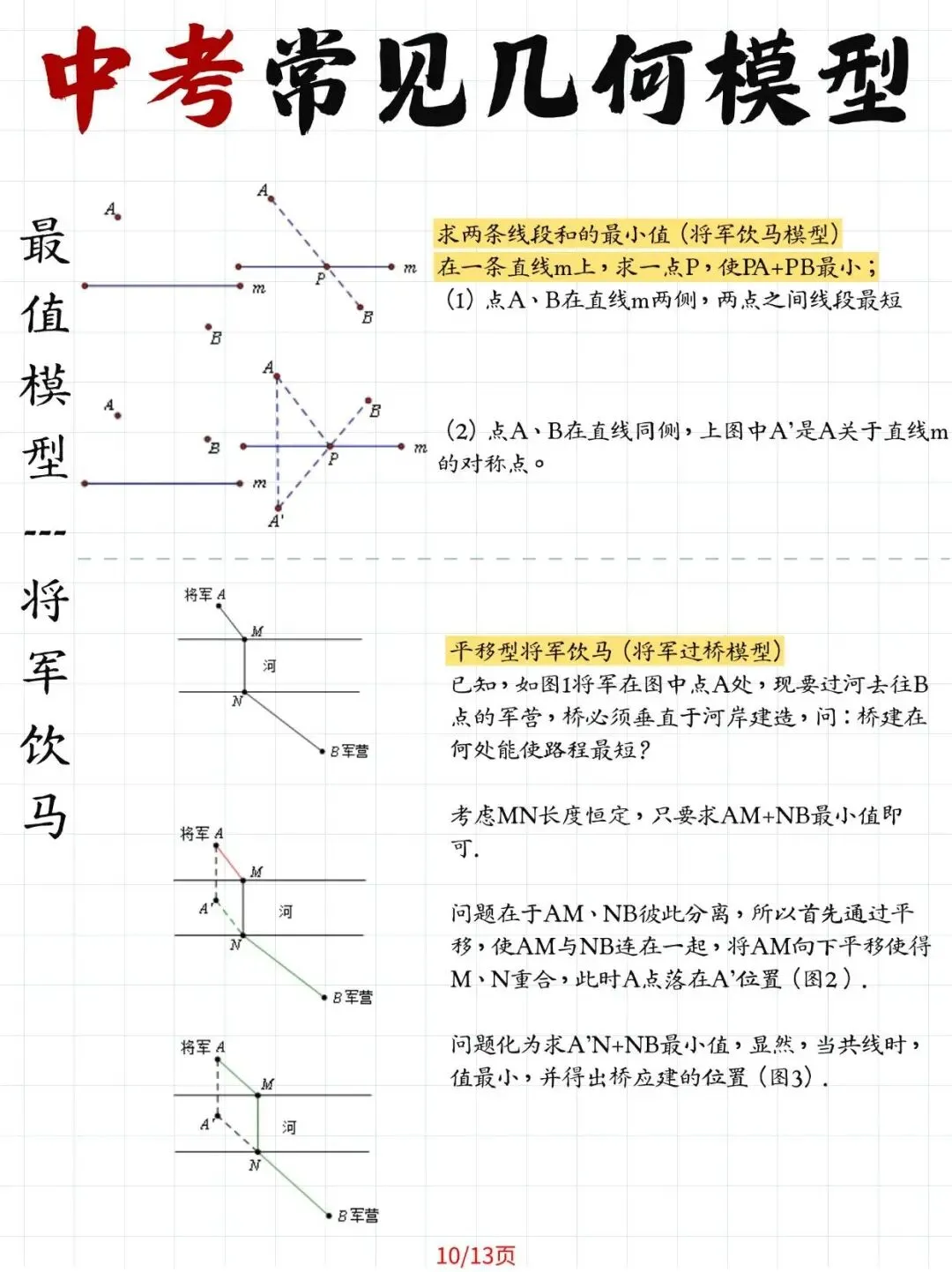
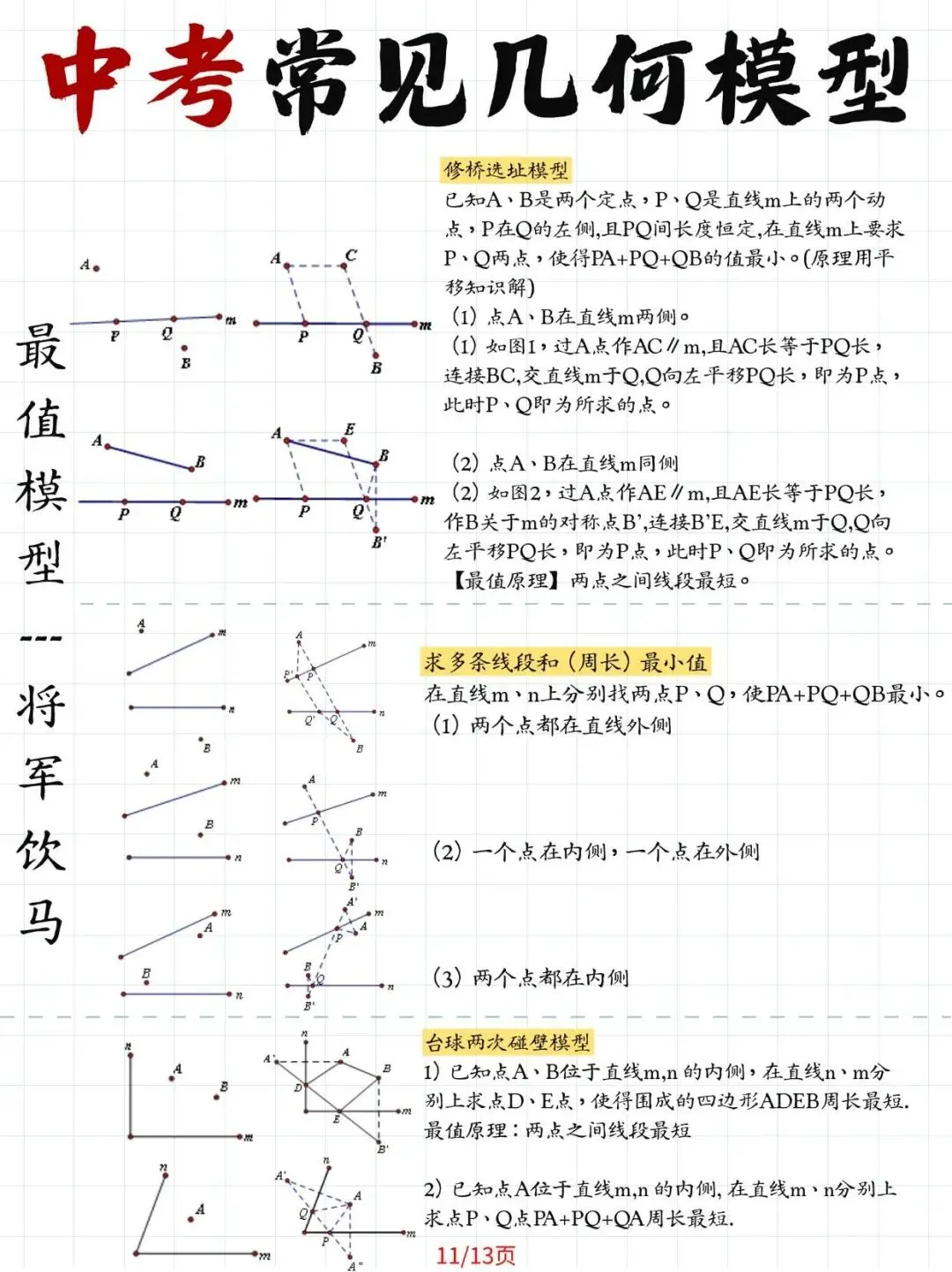
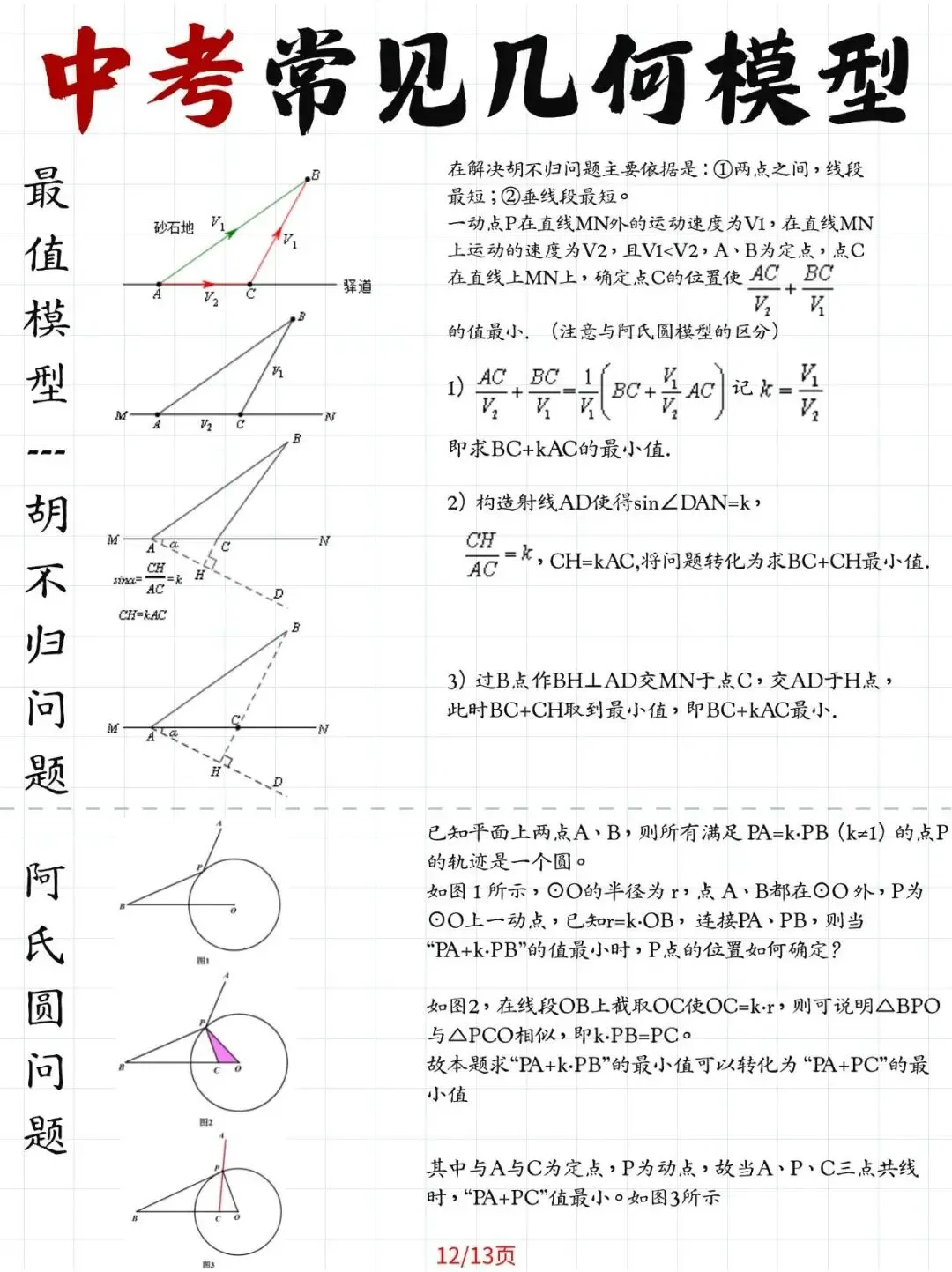
1. 动点最值模型

（1）将军饮马问题：利用轴对称求最短路径，这类问题犹如古代兵法中的智慧结晶。

（2）胡不归模型：通过构造特殊角度的相似三角形求解最值，展现了数学的灵动之美。

2. 图形变换模型

（1）旋转相似：图形旋转后产生新的相似关系，这种动态变化如同万花筒般绚丽多彩。

（2）位似变换：图形按比例放大缩小的变换，在坐标系中尤为常见，解题时需把握位似中心的选取。