(18)2025年上海市中考
奉贤区一模数学第25题
如图1,矩形ABCD中, AB=2BC,
点E在射线BA上,点F在射线BC上,
且DF⊥DE,射线EF与对角线AC交
于点G,与射线DC交于点 M .
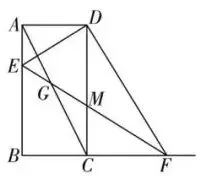
图1
(1)当点E在线段BA上时,
求∠DFM 的正切值,
(2)当G是AC中点时,
求CM/DM的值,
(3)当BC=3,且△DGM与△DCF
相似时,直接写出AE的长.
【解析】(1)∵四边形ABCD是矩形,∴∠DAE=∠ADC
=∠BCD
=90°,
∴∠DAE=∠DCF=90°,
∵ED⊥DF ,
∴∠EDM+∠FDC=90°,
∵∠EDM+∠ADE=90°,
∴∠ADE=∠FDC ,
∴△DAE∽△DCF ,
∴DE/DF=AD/CD,
∵AB=2BC,
∴tan∠DFM=DE/DF
=1/2,
(2)设 DA=x , CM=y ,
∴CD=2x=AB ,
BC=DA=x ,
∴DM=2x- y ,
∵G是AC的中点,
∴EB=DM=2x- y ,
AE=MC=y ,
∵△DCF∽△DAE ,
∴ FC/EA=2,
∴ FC=2y,
∵DC//AB ,
∴FC/MC=FB/EB,
∴2y/y=(x +2y)/(2x- y),
∴ (x +2y)/(2x-y)=2,
∴y=3/4x,
∴ DM=2x-3/4x
=5/4x,
(3)①当点E在线段AB上,如图1,
∵△DGM∽△DCF .
∴∠GDM=∠FDC ,
∵∠ADE=∠FDC
∴∠GDM=∠ADE ,
∵∠GDM=∠BFE ,
∴∠ADE=∠BFE ,
∵ tan∠ADE=AE/AD ,
tan∠BFE=BE/BF,
∴AE/AD=BE/BF,
设 AE=x ,
则 BE =6-x, AD=3,
CF =2x,
∴BF=BC+CF
=3+2x,
∴x/3=(6-x)/(3+2x),
解得: x=(-3+3√5)/2,
(负值舍去),
∴AE=(3√5-3)/2,
②当点E在BA延长线上时,如图2,
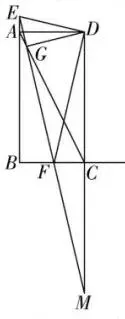
图2
同理: tan∠ADE=tan∠BEF,
∴ AE/AD=BF/BE ,
设 AE=x ,
则 BE=6+x , CF=2x,
∴BF=3-2x,
∴x/3=(3-2x)/(6+x),
解得: x=3√5-6,(负值舍去),
∴ AE=3√5-6,
综上所述:AE=(3√5-3)/2
或 3√5-6.
往期文章






