上海中考 “三科混战” 考题刷屏:当学生想在卷子上写 “我也不会” 时,我看到了教育最好的样子
上海中考 “三科混战” 考题刷屏:当学生想在卷子上写 “我也不会” 时,我看到了教育最好的样子
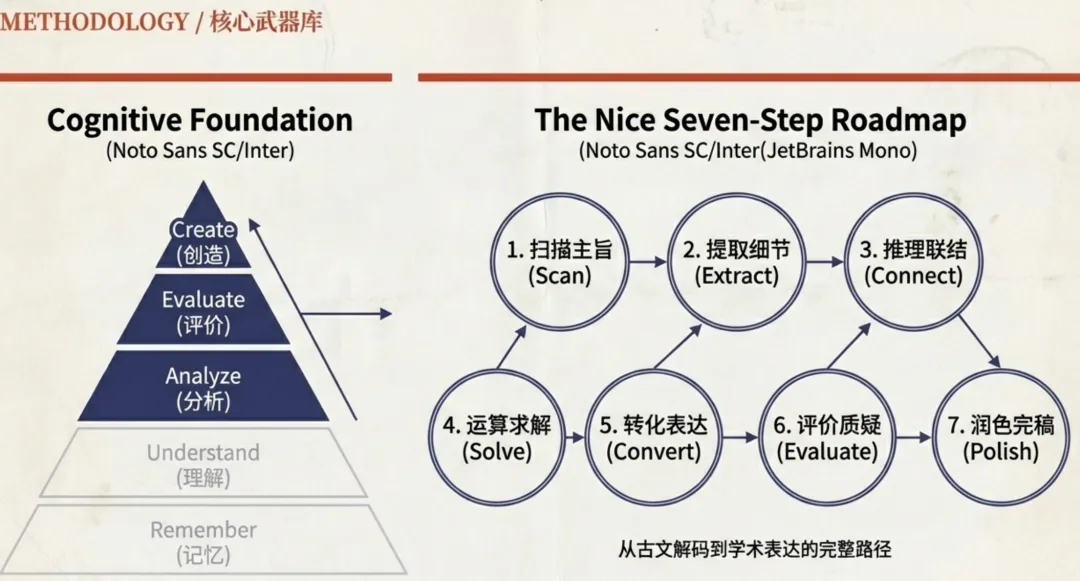
面对超越认知边界的难题,初中生最需要的不是公式,而是 “解决问题的底气” 要求 “李华” 用英文给同学 Peter 回信,解释《九章算术》里的一道题。古文、数学、英语三科混战,很多孩子瞬间 “断电”。 本周课上,有个孩子跑来问我:“老师,这题的数学逻辑已经到高二了,我真算不出来。我能不能在卷子上诚实点写:‘亲爱的 Peter,这题我也不会。但我可以陪你上网查答案,或者请教老师解决问题’?” 全班有些学生大笑,也有一些学生说对啊,题里面说解答题目,也可以寻求帮助啊。 但我没有急着否定,因为这个提问背后,藏着最真实的求知欲,以及面对难题时那份宝贵的诚实。 我告诉孩子们: 诚实地表达 “我不会” 是勇气,但能建设性地提出 “怎么做” 才是底气 。 在标准化考试中,写 “我不会” 可能得不到分;但在真实的人生考场里,能说出 “我目前没答案,但我有方案” 的人,往往走得更远。 面对这种 “魔王级” 跨学科难题,我更想教给学生的,是 “解决问题的思维模型” (The Problem-solving Mindset) 。 为此,我总结了独家的「七步解题法」,带大家层层剥开这道题的逻辑。 【独家干货:Nice 七步解题法】 这套方法对标的是全球公认的布鲁姆认知层次(Bloom's Taxonomy)。我们要做的,是把孩子从简单的 “记忆” 和 “理解”,推向更高阶的 “分析” 与 “创造”。
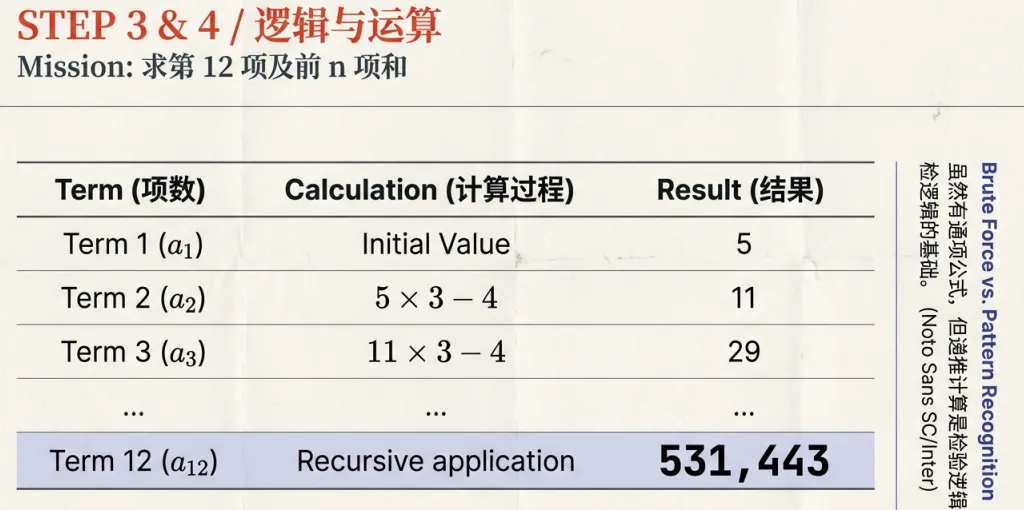
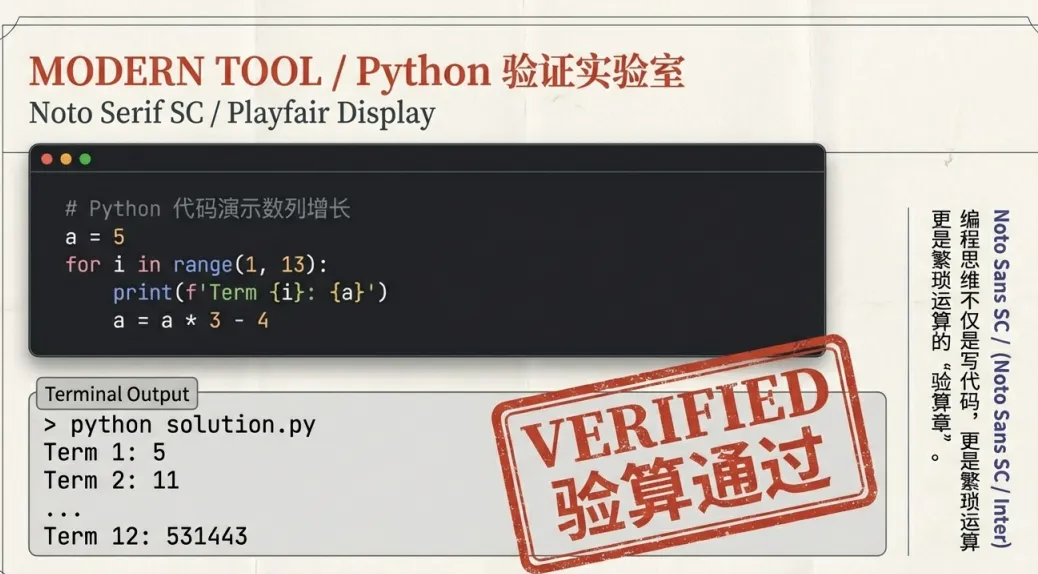
扫描主旨 :快速识别这不仅是写信,而是一篇包裹在故事里的 “数学说明文”。 提取细节 :考验 “解码能力”。将 “初策”“后策” 等古文转化为清晰的逻辑: a n = 3 a n − 1 − 4 。 推理联结 :建立模型。虽然递推数列是高中内容,但我们可以用初中的基础四则运算来拆解。 运算求解 :第 12 项计算结果为: 531 , 443 。前 n 项和规律: 2 3 n + 1 + 4 n − 3 。 转化表达 :这里的难点不在于日常英语,而在于学科语言(Academic Language)。如何精准使用 sequence(数列)、term(项)、multiple(倍数)来串联逻辑。 评价与质疑 :这是区分顶尖人才的关键!运算后发现,题目命题(每项减 1 是 3 的倍数)其实是错误的。 润色完稿 【范文节选:面对题目错误的优雅应变】 "I noticed something interesting. The first term is 5, and 5-1=4, which is not divisible by 3. Perhaps the problem meant to say 'each term minus 2'..."
这种不盲从权威、能够冷静分析并礼貌指正的能力,才是高智商与高情商的结合。
三、 比起教出 “高分”,我更想教出 “双语思考者” 我自己也在不停进修。比起教出一个能精准算出 3^{12}+2 的机器,我更想让孩子们拥有在复杂世界中独立思考的能力。
这种底气来源于:
* 扎实的跨学科积累:懂一点古文背后的科学逻辑。
* 严密的逻辑思维:即便结果错了,推导过程也要清晰。
* 面对权威的从容:当孩子能冷静分析、优雅表达、建设性地质疑时,他们才算真 正掌握了语言。
为什么我一直坚持双语阅读?为什么要推荐用古诗学英文? 因为真正的语言能力,不是 “会说”,而是 “会转换” 。 这道题揭示了翻译链条的真相: 古汉语 → 现代汉语 → 数学逻辑 → 英语表达 。 四步缺一不可。 当孩子的大脑里建立起两套平行的 “知识索引”,当他们能用英文的逻辑框架去理解中文题目,用中文的思考深度去进行英文输出时,他们才算真正拥有了 “思维高速公路” 。 明年,我的 《古诗词双语跨学科课程》 将正式与大家见面。 这一次,我们不只背诗,我们要把古诗词变成 “实验室”: 我不希望孩子在面对复杂世界时,只会说 “我不知道”。 我想教他们说: “虽然我不确定,但我有办法去找到真相。” 如果你是李华,面对这道难题,你会如何优雅地 “求助”?或者你认为,现在的跨学科教育最该教给孩子什么?
版权声明: 本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!