〚中考上海2023-25〛

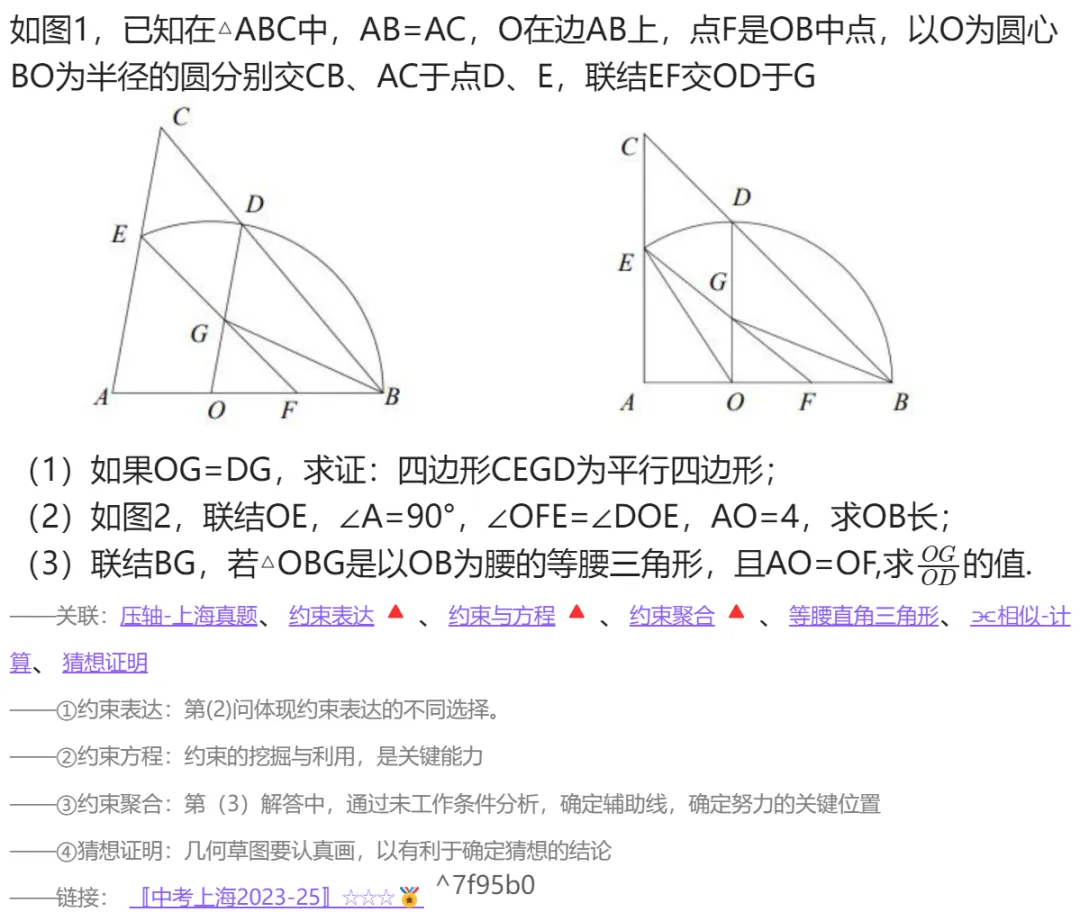
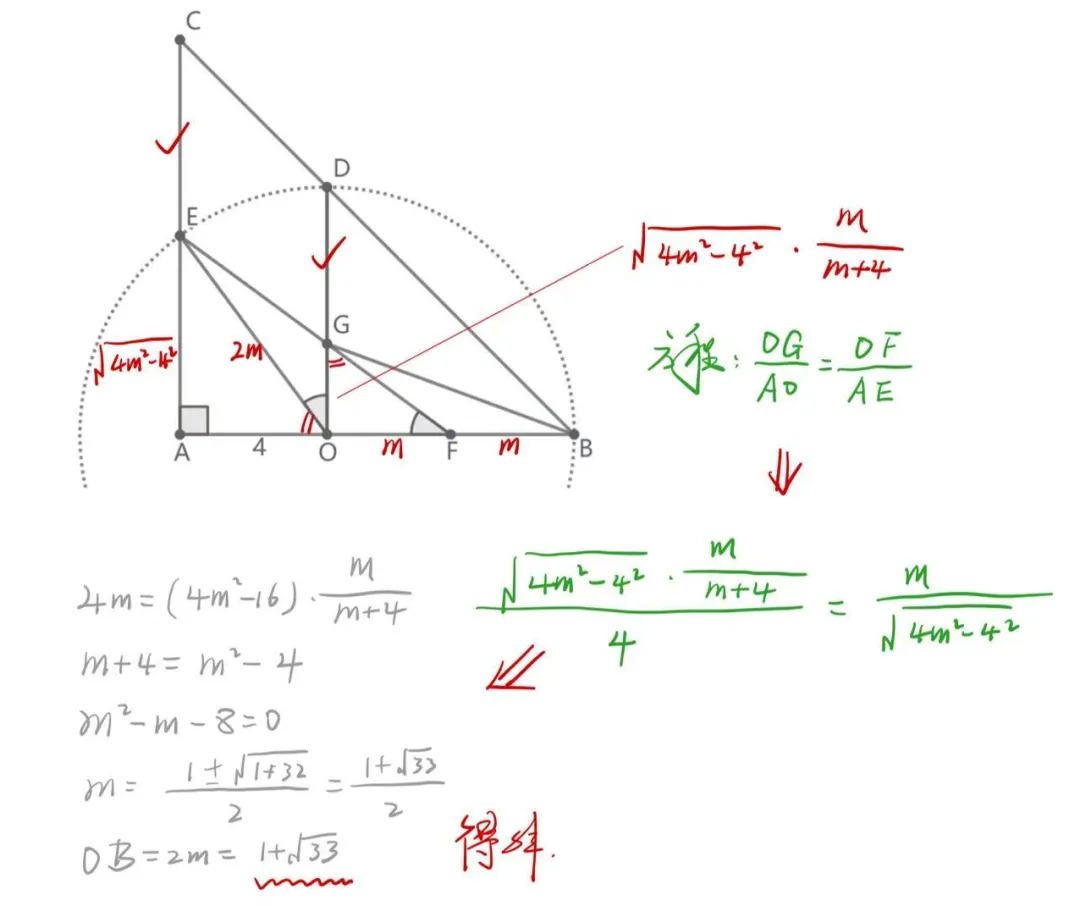
解题思路，如何想到的？

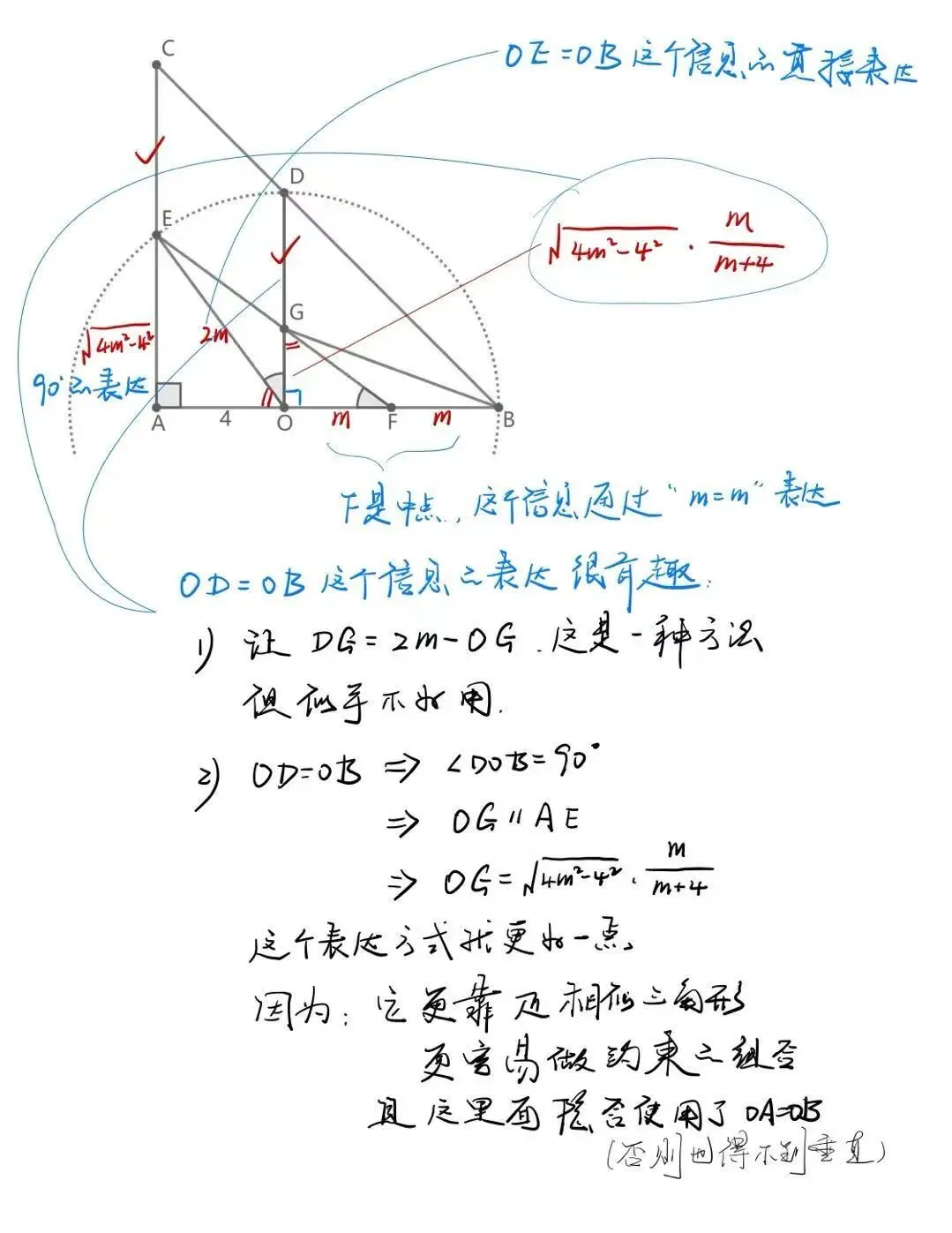
其关键思想：

1. 关于约束表达

   每个条件，每个，都要合适的发挥作用

   ——因此，如果解题陷入困境，去检查是否所有条件都有工作

   约束条件发挥作用的途径并不唯一。

   ——因此在做约束表达式，要多想想，找最好用的那个

   约束条件发挥作用的方式有两大类

   ——其一，用于逻辑推理

   ——其二，用于数值计算

   这里是第2种。数值计算也是逻辑推理，特殊的逻辑推理。由于太特殊，故单列一项。

   两者并不严格区分，比如即便计算，多数条件是作用于推理，间接用于计算。比如OA=OB这个条件。  ^73cadb

2. 约束方程，是解题的最终手段。

   注意约束条件的挖掘与使用，约束条件多多益善，留最后一个用于方程。

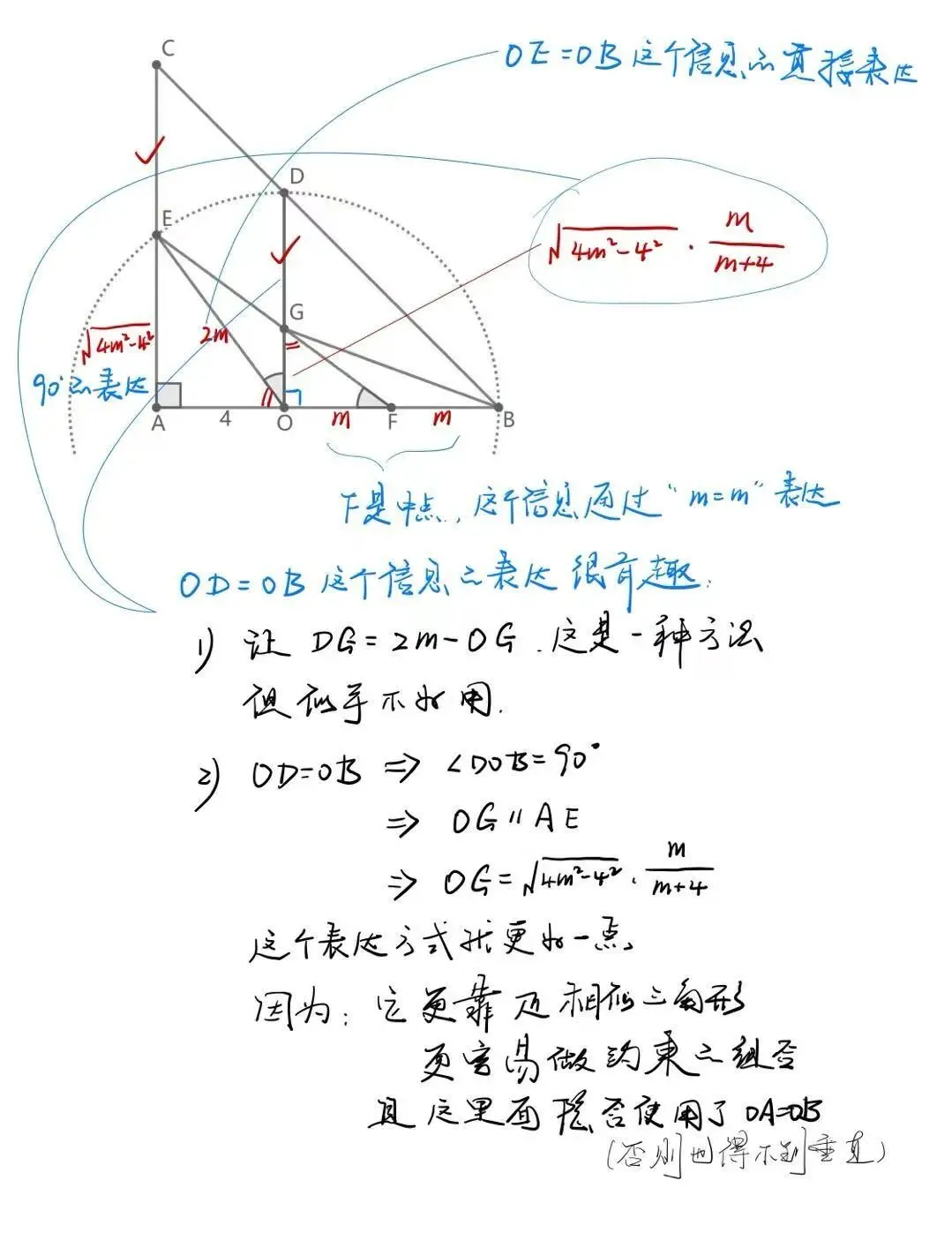
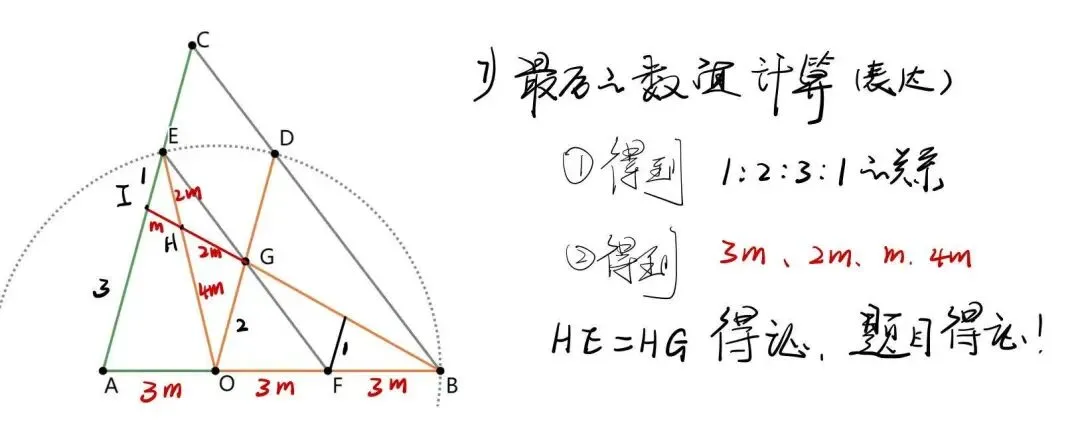
以上解题中，关键点、难点是什么？

1. 辅助线，是最关键的一部分

2. 辅助线，是怎么想到的？最主要的思维是：[[约束聚合-主动正推]]

   ——更多条件所在位置，特别是未工作条件的位置，是思考的重点

3. 猜想与证明。对结论有个预设值，这里是最后的结论，相对容易处理。中间结论的猜想，相对更难。

本号关注

①-基础数学能力（留痕阅读、数学表达、正推倒推、猜想证明...）；

②-数学与数学学习认知； 

③-数学知识的底层逻辑及结构化、系统化、规则化； 

④-数学思维（抽象、简化、约束、链接）； 

⑤-数学思想（特征思想、约束转化、分步思想、同构思想、一一对应、面积法...)

以及，少量个人生活的琐碎点滴