2025年四川省绵阳市中考数学试卷
一、选择题:本大题共12个小题,每小题3分,共36分.每个小题只有一个选项符合题目要求。
1.(3分)﹣7的相反数是( )
A.﹣7B.7C.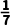 D.
D.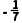
2.(3分)下列图形中,既是中心对称图形又是轴对称图形的是( )

3.(3分)据国内AI产品榜统计数据,某款AI搜索工具在上线仅20天后,其日活跃用户数(DAU)迅速突破两千万大关,达22150000.将数据22150000用科学记数法表示为( )
A.0.2215×107B.2.215×106
C.22.15×106D.2.215×107
4.(3分)若x是任意实数,则下列各式一定有意义的是( )
A.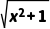 B.
B.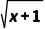 C.
C.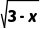 D.
D.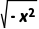
5.(3分)如图所示几何体,由5个完全相同的正方体组合而成,它的主视图是( )
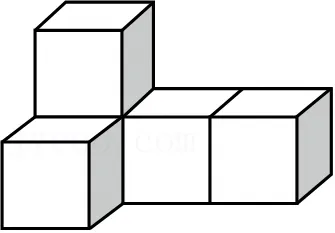

6.(3分)设a>b,则下列不等关系正确的是( )
A.a+3<b+3B.﹣2a>﹣2bC.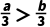 D.a﹣3<b﹣3
D.a﹣3<b﹣3
7.(3分)我国元朝朱世杰所著的《算学启蒙》中,记载了这样一个问题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”其大意是:跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,问快马几天可追上慢马?据此可知快马追上慢马的天数是( )
A.5天B.10天C.15天D.20天
8.(3分)如图,在平面直角坐标系中,等边△ABC的顶点A(1,0),C(1,2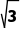 ),将△ABC向左平移1个单位长度,则平移后点B的坐标为( )
),将△ABC向左平移1个单位长度,则平移后点B的坐标为( )
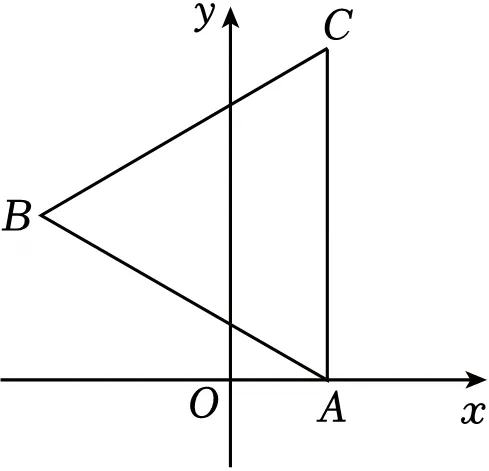
A.(﹣3,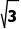 )B.(
)B.(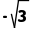 ,3)C.(
,3)C.(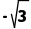 ,2)D.(﹣2,
,2)D.(﹣2,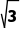 )
)
9.(3分)观察下列单项式:﹣xy,x2y3,﹣x3y5,x4y7,⋯,探究发现其中规律,你认为从左到右第15个单项式是( )
A.﹣x15y27B.﹣x15y29C.x13y27D.x13y29
10.(3分)如图,在正方形ABCD中,点E在BC的延长线上,点F是CD的中点,连接EF并延长交AD于点G,连接BF,BG,AB=4CE=4,则tan∠FBG=( )
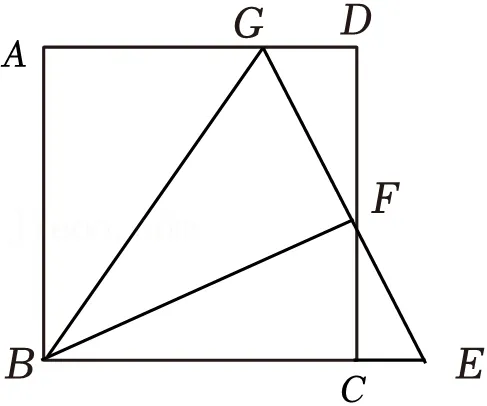
A.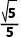 B.
B.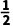 C.
C.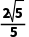 D.2
D.2
11.(3分)随着人工智能的快速发展,机器人的工作效率越来越高,为我们的工作和生活带来了许多便利.厂家将一款普通机器人升级改造为智能机器人,智能机器人的工作效率是普通机器人的1.5倍.若两种机器人分别同时装载货物6吨,普通机器人比智能机器人多用20分钟,则智能机器人每小时可以装载货物( )
A.0.1吨B.0.15吨C.6吨D.9吨
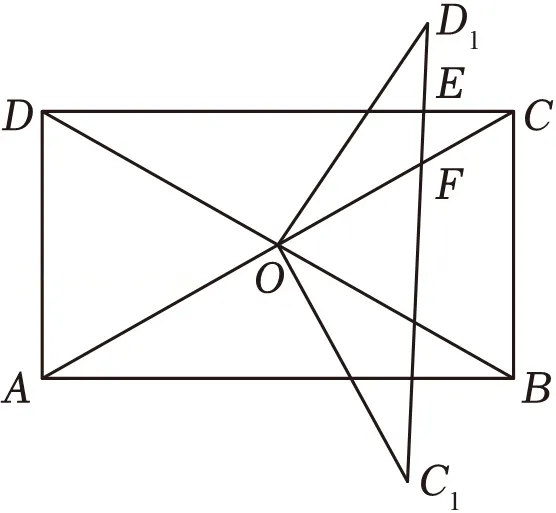
12.(3分)如图,矩形ABCD的对角线AC,BD相交于点O,AB=4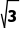 =4,将△OCD绕点O顺时针旋转至△OC1D1,C1D1与CD,OC分别交于点E,F,当CE
=4,将△OCD绕点O顺时针旋转至△OC1D1,C1D1与CD,OC分别交于点E,F,当CE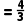 时,△OFC1的周长为( )
时,△OFC1的周长为( )
A.4+4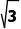 B.6+3
B.6+3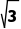 C.8+2
C.8+2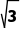 D.10
D.10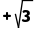
二、填空题:本大题共6个小题,每小题4分,共24分.将答案填写在答题卡相应的横线上。
13.(4分)因式分解:x2﹣1= .
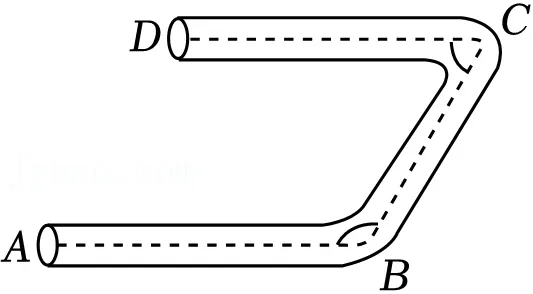
14.(4分)如图,在一个弯形管道ABCD中,已知拐角∠BCD=60°,管道AB∥CD,则∠ABC= °.
15.(4分)若关于x的一元二次方程x2﹣6x+a=0的一个根为1,则a的值为 .
16.(4分)水是生命之源.水分子的化学式为H2O,即1个水分子H2O由2个氢原子H和1个氧原子O组成.现有形状大小完全相同的4张卡片,分别有H,H,O,O图案,小明从打乱的这4张卡片中随机任取3张,则这三张卡片对应的元素符号恰能组成水分子化学式的概率是 .
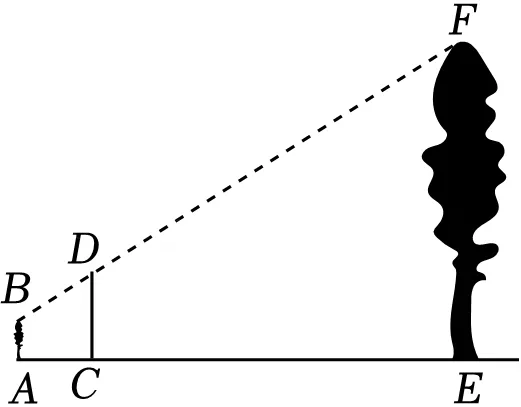
17.(4分)如图,小明在课外实践活动中对一棵大树的高度进行测量.他准备了一根竹竿,将竹竿垂直固定于离大树10m远的C处,然后沿着大树底部E和竹竿底部C所在水平直线由C点后退2m至A点时,看大树顶部F视线恰好经过竹竿的顶端D,测得小明的眼睛距地面的高度AB为1.6m,竹竿CD长3m,则大树的高度EF为m.
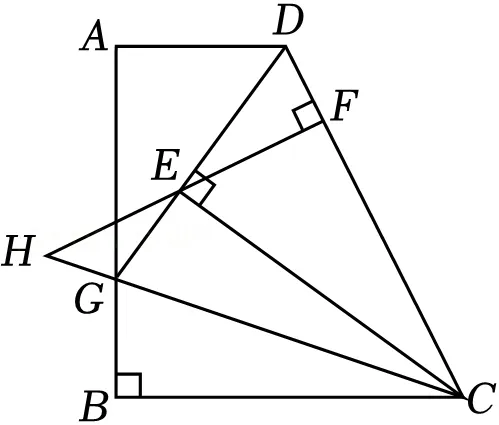
18.(4分)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,BC=4,AD=2,点E在四边形内,DE⊥CE,EF⊥CD于点F,将△BCG沿CG翻折,点B恰好与点E重合,延长FE交折痕CG的延长线于点H,∠DCG=45°,则点B到直线FH的距离为 .
三、解答题。
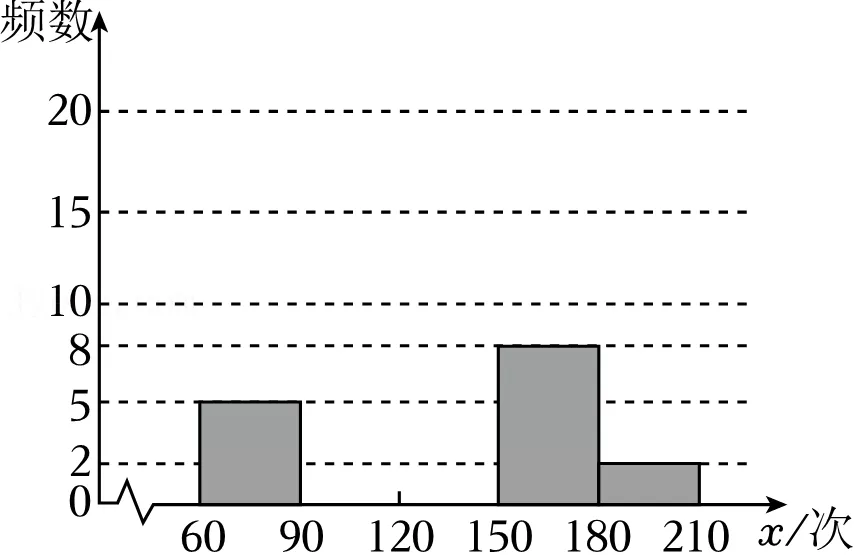
19.(12分)为促进学生健康成长,提高身体素质,红星中学积极开展丰富多彩的体育活动.为了解该校800名学生1分钟跳绳的情况,随机抽取了50名学生1分钟的跳绳次数(次数用x表示,单位:次),将其分成以下五组:60≤x<90,90≤x<120,120≤x<150,150≤x<180,180≤x<210,并绘制成不完整的频数分布直方图,部分信息如下:
1分钟的跳绳次数在90≤x<120中的具体数据为92,97,99,103,105,105,105,110,113,113,114,115,115,117,119.
根据以上信息,解答下列问题:
(1)1分钟的跳绳次数在90≤x<120范围内的众数是 次,中位数是 次;
(2)补全频数分布直方图;
(3)请估计该校学生1分钟的跳绳次数不低于120次的人数.
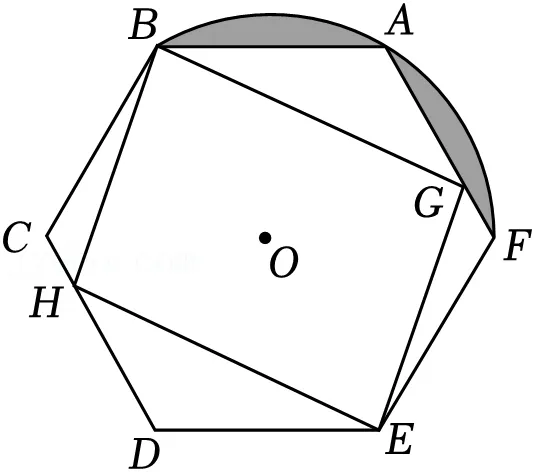
20.(12分)如图,在中心为O的正六边形ABCDEF中,点G,H分别在边AF,CD上,且不同于正六边形的顶点,CH=FG.
(1)证明:四边形BGEH为平行四边形;
(2)若正六边形的边长为4,以点O为圆心,OB为半径的扇形BOF与正六边形形成阴影部分,求图中阴影部分的面积.
21.(12分)某学校摄影社到商场购买A,B两种不同型号的相册,商场的销售方式为以下两种:
①一次性购买A型相册不超过20本,按照零售价销售;超过20本时,超过部分每本的价格比零售价低6元销售.
②一次性购买B型相册不超过15本,按照零售价销售;超过15本时,超过部分每本的价格比零售价低4元销售.
若购买30本A型相册和10本B型相册,共需支付2240元;若购买20本A型相册和40本B型相册,共需支付3100元.
(1)这家商场A,B型相册每本的零售价分别是多少元?
(2)若该社团计划购买A型和B型相册共15本,要求A型相册数量大于或等于B型相册数量的2倍,且总费用不超过870元,请你设计购买方案,并写出所需费用最少的购买方案.
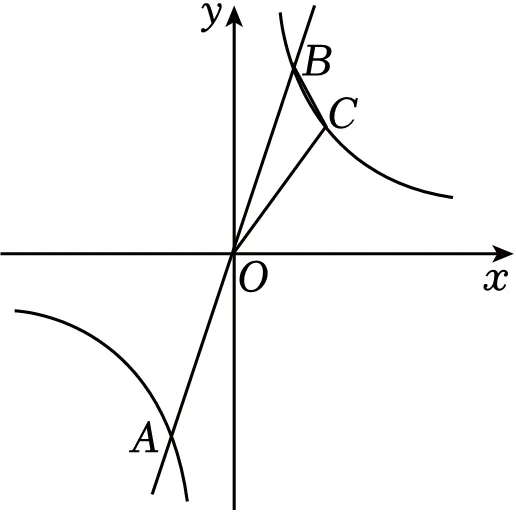
22.(12分)如图,在平面直角坐标系中,正比例函数y=mx(m≠0)的图象与反比例函数y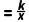 (k≠0)的图象交于A(﹣2,m﹣9),B两点,点C在反比例函数的图象上,且在第一象限内点B的右侧,连接BC,OC,△BOC的面积为5.
(k≠0)的图象交于A(﹣2,m﹣9),B两点,点C在反比例函数的图象上,且在第一象限内点B的右侧,连接BC,OC,△BOC的面积为5.
(1)求点A,B的坐标及反比例函数的解析式;
(2)探究在x轴上是否存在点M,使得以点O,C,M,N为顶点的四边形为菱形?若存在,求出点N的坐标;若不存在,请说明理由.
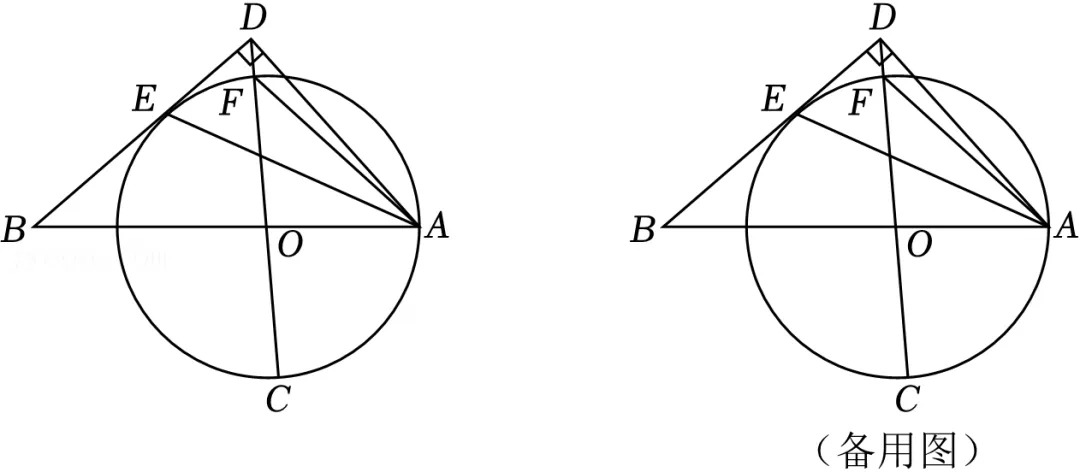
23.(12分)如图,点A,C在⊙O上,连接AO,CO并延长,分别与⊙O的切线相交于点B,点D,切点为E,CD与⊙O交于点F,连接AE,AF,AD⊥BD,垂足为点D,DE=3,DF=1.
(1)求证:AE平分∠BAD;
(2)设AB=kOB(k>0),求k的值;
(3)求cos∠EAF的值.
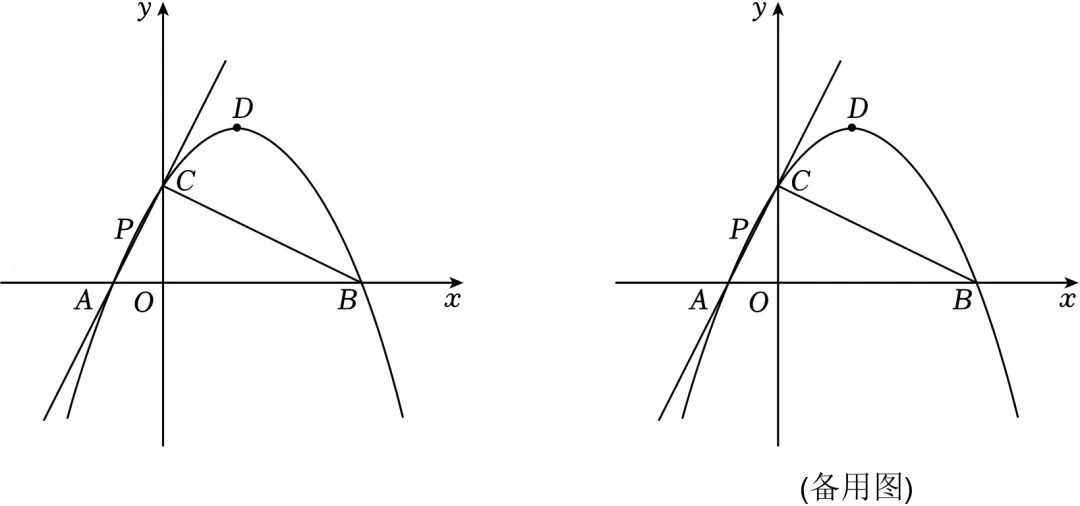
24.(14分)如图,在平面直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点C,点B在y轴右侧的x轴上,抛物线y=ax2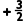 x+c(a≠0)经过A,B,C三点,顶点为D.
x+c(a≠0)经过A,B,C三点,顶点为D.
(1)求抛物线的解析式及点B,D的坐标;
(2)点P在直线AC上运动,当△BDP的周长最小时,求点P的坐标;
(3)探究在△ABC内部能否截出面积最大的矩形EFGH(顶点E,F,G,H在△ABC各边上)?若能,求出此时矩形在AB边上的顶点的坐标;若不能,请说明理由.
2025年四川省绵阳市中考数学试卷
参考答案与每一道试题解析见网盘免费下载

我用夸克网盘给你分享了「2025年四川省绵阳市中考数学试卷.docx」,点击链接或复制整段内容,打开「夸克APP」即可获取。
/~ce8e39xuzH~:/
链接:https://pan.quark.cn/s/69e4b8873065?pwd=94KH
提取码:94KH



![[济南专版] | 资深教师整理:济南中考语文一模近3年“必考题型”分类汇编 [济南专版] | 资深教师整理:济南中考语文一模近3年“必考题型”分类汇编](https://sjds.net/zb_users/cache/thumbs/575fce53426f71fd437d3b40b88c5a3d-320-200-1.gif)

![[济南专版] | 直击考点!济南近3年中考一模语文真题分类汇编 [济南专版] | 直击考点!济南近3年中考一模语文真题分类汇编](https://sjds.net/zb_users/cache/thumbs/f0cba845975a0cf0e65c590e972517ca-320-200-1.gif)

