小
学
点击上方卡片关注，免费领学习资料
【专题解析】
英国科学家牛顿在他的《普通算术》一书中，有一道关于牛在牧场上吃草的问题，即牛在牧场上吃草，牧场上的草在不断的、均匀的生长．后人把这类问题称为牛吃草问题或叫做“牛顿问题”．
“牛吃草”问题主要涉及三个量：草的数量、牛的头数、时间．难点在于随着时间的增长，草也在按不变的速度均匀生长，所以草的总量不定．“牛吃草”问题是小学应用题中的难点．
解“牛吃草”问题的主要依据：
①草的每天生长量不变；
②每头牛每天的食草量不变；
③草的总量
草场原有的草量
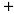新生的草量，其中草场原有的草量是一个固定值
④新生的草量每天生长量
天数．
同一片牧场中的“牛吃草”问题，一般的解法可总结为：
⑴设定1头牛1天吃草量为“1”；
⑵草的生长速度(对应牛的头数较多天数
对应牛的头数较少天数)
(较多天数较少天数)；
⑶原来的草量对应牛的头数吃的天数草的生长速度吃的天数；
⑷吃的天数原来的草量(牛的头数草的生长速度)；
⑸牛的头数原来的草量吃的天数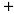草的生长速度．
“牛吃草”问题有很多的变例，像抽水问题、检票口检票问题等等，只有理解了“牛吃草”问题的本质和解题思路，才能以不变应万变，轻松解决此类问题．
【例题1】
牧场上有一片匀速生长的草地，可供27头牛吃6周，或供23头牛吃9周，那么它可供多少头牛吃18周？
解析：设1头牛1周的吃草量为“1”，
草的生长速度为 (23×9-27×6)÷(9-6)=15 ，
原有草量为(27-15)×6=72，
可供72÷18+15=19（头）牛吃18周。
练习1
1、一片草地，每天都匀速长出青草，如果可供24头牛吃6天，20头牛吃10天，那么可供19头牛吃几天？
答案：每天长草量：（20×10-24×6）÷（10-6）=14（份）
原有草量：24×6-14×6=60（份）
可吃天数：60÷（19-14）=12（天）
2、牧场上一片草地，每天牧草都匀速生长，这片牧草可供10头牛吃20天，或者可供15头牛吃10天，问可供25头牛吃几天？
答案：每天长草量：（20×10-15×10）÷（20-10）=5（份）
原有草量：（10-5）×20=100（份）
可吃天数：100÷（25-5）=5（天）
3、牧场上的青草每天都在匀速生长，这片青草可供27头牛吃6周或23头牛吃9周，那么这片草地可供21头牛吃几周？
答案：每天长草量：（23×9-27×6）÷（9-6）=15（份）
原有草量：（27-15）×6=72（份）
可吃时间：72÷（21-15）=12（周）
【例题2】
由于天气逐渐冷起来，牧场上的草不仅不长，反而以固定的速度在减少。如果某块草地上的草可供25头牛吃4天，或可供16头牛吃6天，那么可供多少头牛吃12天？
解析: 设1头牛1天吃的草为“1”。
牧场上的草每天自然减少 (25×4-16×6)÷(6-4)=2；
原来牧场有草(25+2)×4=108，
12天吃完需要牛的头数是：108÷12-2=7 (头)
练习2：
1、由于天气逐渐冷起来，牧场上的草每天以均匀的速度在减少。经计算，牧场上的草可供20头牛吃5天或可供16头牛吃6天。那么，可供11头牛吃几天？
答案：每天减少量：（20×5-16×6）÷（6-5）=4（份）
原有草量：（20+4）×5=120（份）
可吃天数：120÷（11+4）=8（天）
2、由于天气逐渐冷起来，牧场上的草以固定速度在减少。已知牧场上的草可供33头牛吃5天或可供24头牛吃6天。照此计算，这个牧场可供多少头牛吃10天？
答案：每天减少量：（33×5-24×6）÷（6-5）=21（份）
原有草量：（33+21）×5=270（份）
牛的数量：270÷10-21=6（头）
3、经测算，地球上的资源可供100亿人生活100年，或可供80亿人生活300年。假设地球新生成的资源增长速度是一样的，那么，为满足人类不断发展的需要，地球最多能养活多少亿人？
答案：（80×300-100×100）÷（300-100）=70（亿）
【例题3】
自动扶梯以均匀速度由下往上行驶着，两位性急的孩子要从扶梯上楼。已知男孩每分钟走20级台阶，女孩每分钟走15级台阶，结果男孩用5分钟到达楼上，女孩用了6分钟到达楼上。问：该扶梯共有多少级台阶？
解析：与前两个题比较，“总的草量”变成了“扶梯的台阶总数”，“草”变成了“台阶”，“牛”变成了“速度”，也可以看成是牛吃草问题。
上楼的速度可以分为两部分：一部分是男、女孩自己的速度，另一部分是自动扶梯的速度。男孩5分钟走了20×5=100（级），女孩6分钟走了15×6=90（级），女孩比男孩少走了100—90=10（级），多用了6—5=1（分钟），说明电梯1分钟走10级。因男孩5分钟到达楼上，他上楼的速度是自己的速度与扶梯的速度之和。所以，扶梯共有（20+10）×5=150（级）
练习3：
1、自动扶梯以均匀速度行驶着，渺小明和小红从扶梯上楼。已知小明每分钟走25级台阶，小红每分钟走20级台阶，结果小明用5分钟，小红用了6分钟分别到达楼上。该扶梯共有多少级台阶？
答案：扶梯每分钟上行：（25×5-20×6）÷（6-5）=5（级）
扶梯共有台阶数：（25+5）×5=150（级）
2、两个顽皮的孩子逆着自动扶梯的方向行走。在20秒钟里，男孩可走27级台阶，女孩可走24级台阶，男孩走了2分钟到达另一端，女孩走了3分钟到达另一端，该扶梯共有多少级台阶？
答案：扶梯每分钟上行：[24×（180÷20）-27×（120÷20）]÷（3-2）=54（级）
扶梯共有台阶数：27×（120÷20）-54×2=54（级）
3、两只蜗牛由于耐不住阳光的照射，从井顶逃向井底。白天往下爬，两只蜗牛白天爬行的速度是不同的。一只每天白天爬20分米，另一只爬15分米。黑夜里往下滑，两只蜗牛滑行的速度却是相同的。结果一只蜗牛恰好用了5个昼夜到达井底，另一只蜗牛恰好用了6个昼夜到达井底。那么，井深多少米？
答案：每夜下滑：（20×5-15×6）÷（6-5）=10（分米）
井深：（20+10）×5=150（分米）=15（米）
【例题4】
一只船发现漏水时，已经进了一些水，水匀速进入船内.如果10人淘水，3小时淘完；如5人淘水，8小时淘完.如果要求2小时淘完，要安排多少人淘水？
解析：设1人1小时淘出的水量是“1”，
淘水速度是(5×8-10×3)÷(8-3)=2，
原有水量(10-2)×3=24，
要求2小时淘完，要安排24÷2+2=14人淘水
练习4：
1、有一水池，池底有泉水不断涌出。用10部抽水机20小时可以把水抽干，用15部相同的抽水机10小时可以把水抽干。那么用25部这样的抽水机多少小时可以把水抽干？
答案：每小时涌出水：（10×20-15×10）÷（20-10）=5（份）
原有泉水：（10-5）×20=100（份）
抽干需要：100÷（25-5）=5（时）
2、有一个长方形的水箱，上面有一个注水孔，底面有一个出水孔，两孔同时打开后，如果每小时注水30立方分米，7小时可以注满水箱；如果每小时注水45立方分米，注满水箱可少用2.5小时。那么每小时由底面小孔排出多少立方分米的水（设每小时排水量相同）？
答案：[30×7-45×（7-2.5）]÷2.5=3（立方分米）
3、有一水井，连续不段涌出泉水，每分钟涌出的水量相等。如果用3台抽水机来抽水，36分钟可以抽完；如果使用5台抽水机，20分钟抽完。现在12分钟内要抽完井水，需要抽水机多少台？
答案：每小时涌出水（3×36-5×20）÷（36-20）=1/2（份）
原有泉水：（3-1/2）×36=90（份）
抽干需要抽水机：（90+1/2×12）÷12=8（台）
【例题5】
有三块草地，面积分别为5，6，和8公顷。草地上的草一样厚，而且长得一样快。第一块草荐地可供11头牛吃10天，第二块草地可供12头牛吃14天。问第三块草地可供19头牛吃多少天？
解析：前几道题我们接触的是在同一块草地上，同一个水池中，现在是三块面积不同的草地。为了解决这个问题，只需将三块草地的面积统一起来。即[5，6，8]=120
这样，第一块5公顷可供11头牛吃10天，120÷5=24，变为120公顷草地可供11×24=264（头）牛吃10天
第二块6公顷可供12头牛吃14天，120÷6=20，变为120公顷草地可供12×20=240（头）牛吃14天。
120÷8=15。
问题变成：120公顷草地可供19×15=285（头）牛吃几天？
因为草地面积相同，可忽略具体公顷数，原题可变为：
一块草地匀速生长，可供264头牛吃10天或供240头牛吃14天，那么可供285头牛齿及天？即
每天新长出的草：（240×14—264×10）÷（14—10）=180（份）
草地原有草：（264—180）×10=840（份）
可供285头牛吃的时间：840÷（285—180）=8（天）
答：第三块草地可供19头牛吃8天。
练习5：
1、某车站在检票前若干分钟就开始排队，每分钟来的旅客人数一样多。从开始检票到等候检票的队伍消失，同时开4个检票口需30分钟，同时开5个检票口需20分钟。如果同时打开7个检票口，那么需多少分钟？
答案：每小时旅客增加：（4×30-5×20）÷（30-20）=2（份）
原有旅客：（4-2）×30=60（份）
需要时间：60÷（7-2）=12（分钟）
2、快、中、慢三车同时从A地出发，追赶一辆正在行驶的自行车，三车的速度分别是嵋小时24千米、20千米、19千米。快车追上自行车用了6小时，中车追上自行车用了10小时，慢车追上自行车用多少小时？
答案：货车速度：（20×10-24×6）÷（10-6）=14（千米/时）
三车出发时货车距A地：（24-14）×6=60（千米）
慢车追上货车的时间：60÷（19-14）=12（时）
3、一个牧场上的青草每天都匀速生长。这片青草可供17头牛吃30天，或供19头牛吃24天。现有一群牛吃了6天后卖掉4头，余下的牛又吃了2天将草吃完。这群牛原来有多少头？
答案：青草每天长出：（17×30-19×24）÷（30-24）=9（份）
原有青草：（17-9）×30=240（份）
假设4头牛不卖，一共吃掉青草：240+9×（6+2）+4×2=320（份）
这群牛原来有：320÷（6+2）=40（头）
40讲目录如下
第1讲 定义新运算
第2讲 简便运算(一 )
第3讲 简便运算(二)
第4讲 简便运算(三)
第5讲 简便运算(四)
第6讲 转化单位"1" (一)
第7讲 转化单位”1" (二)
第8讲 转化单位"1" (三)
第9讲 设数法解题
第10讲 假设法解题(一)
第11讲 假设法解题(二)
第12讲 倒推法解题
第13讲 代数法解题
第14讲 比的应用(一)
第15讲 比的应用(二)
第16讲 工程问题
第17讲 浓度问题
第18讲 面积计算(一 )
第19讲 面积计算(二)
第20讲 面积计算( 三)
第21讲 "不变量”解题
第22讲 特殊工程问题
第23讲 周期工程问题
第24讲 比较大小
第25讲 最大最小问题
第26讲 乘法和加法原理
第27讲 表面积与体积(一)
第28讲 表面积与体积(二)
第29讲 抽屉原理(一 )
第30讲 抽屉原理(二 )
第31讲 逻辑推理(一)
第32讲 逻辑推理(二)
第33讲 行程问题(一)
第34讲 行程问题(二)
第35讲 行程问题(三)
第36讲 流水行船问题
第37讲 对策问题
第38讲 应用同余问题
第39讲 “牛吃草”问题
第40讲 不定方程
六年级教师用书
下载电子版资料方式
▲关注"小学数学思维每日一练"
发送消息"六年级1"
即可免费领取电子版打印
点击阅读原文
查看近期每日一练及答案汇总
