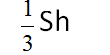一、长度单位是用来测量物体的长度的。

常用的长度单位有：

千米、米、分米、厘米、毫米。

 二、长度单位：

1千米=1000米

1米=10分米

1分米=10厘米

1厘米=10毫米

1米=100厘米

1米=1000毫米

三、面积单位是用来测量物体的表面或平面图形的大小的。

常用面积单位：

平方千米、公顷、平方米、平方分米、平方厘米。

四、测量和计算土地面积，通常用公顷作单位。

边长100米的正方形土地，面积是1公顷。

五、测量和计算大面积的土地，通常用平方千米作单位。

边长1000米的正方形土地，面积是1平方千米。

六、面积单位：（100）

1平方千米=100公顷

1公顷=10000平方米

1平方米=100平方分米

1平方分米=100平方厘米

七、体积单位是用来测量物体所占空间的大小的。

常用的体积单位有：

立方米、立方分米（升）、立方厘米（毫升）。

八、体积单位：（1000）

1立方米=1000立方分米

1立方分米=1000立方厘米

1升=1000毫升

九、常用的质量单位有：

吨、千克、克。

十、质量单位：

1吨=1000千克

1千克=1000克

十一、常用的时间单位有：

世纪、年、季度、月、旬、日、时、分、秒。

十二、时间单位：

1世纪=100年

1年=12个月

1年=4个季度

1个季度=3个月

1个月=3旬

大月=31天

小月=30天

平年二月=28天

闰年二月=29天

1天=24小时

1小时=60分

1分=60秒

十三、高级单位的名数改写成低级单位的名数应该乘以进率；低级单位的名数改写成高级单位的名数应该除以进率。

十四、常用计量单位用字母表示：

一、用直尺把两点连接起来，就得到一条线段；把线段的一端无限延长，可以得到一条射线；把线段的两端无限延长，可以得到一条直线。

线段、射线都是直线上的一部分。

线段有两个端点，长度是有限的；射线只有一个端点，直线没有端点，射线和直线都是无限长的。

二、从一点引出两条射线，就组成了一个角。

角的大小与两边叉开的大小有关，与边的长短无关。角的大小的计量单位是（°）。

三、角的分类：

小于90度的角是锐角；等于90度的角是直角；大于90度小于180度的角是钝角；等于180度的角是平角；等于360度的角是周角。

四、相交成直角的两条直线互相垂直；在同一平面不相交的两条直线互相平行。

五、三角形是由三条线段围成的图形。

围成三角形的每条线段叫做三角形的边，每两条线段的交点叫做三角形的顶点。

六、三角形按角分，可以分为锐角三角形、直角三角形和钝角三角形。

按边分，可以分为等边三角形、等腰三角形和任意三角形。

七、三角形的内角和等于180度。

八、在一个三角形中，任意两边之和大于第三边。

九、在一个三角形中，最多只有一个直角或最多只有一个钝角。

十、四边形是由四条边围成的图形。常见的特殊四边形有：平行四边形、长方形、正方形、梯形。

十一、圆是一种曲线图形。

圆上的任意一点到圆心的距离都相等，这个距离就是圆的半径的长。

通过圆心并且两端都在圆的线段叫做圆的直径。

十二、有一些图形，把它沿着一条直线对折，直线两侧的图形能够完全重合，这样的图形就是轴对称图形。

这条直线叫做对称轴。

十三、围成一个图形的所有边长的总和就是这个图形的周长。

十四、物体的表面或围成的平面图形的大小，叫做它们的面积。

十五、平面图形的面积计算公式推导：

【1】平行四边形面积公式的推导过程？

① 把平行四边形通过剪切、平移可以转化成一个长方形。

② 长方形的长等于平行四边形的底，长方形的宽等于平行四边形的高，长方形的面积等于平行四边形的面积。

③ 因为：长方形面积=长×宽，所以：平行四边形面积=底×高。即：S=ah。

【2】三角形面积公式的推导过程？

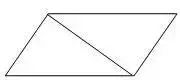
① 用两个完全一样的三角形可以拼成一个平行四边形。

② 平行四边形的底等于三角形的底，平行四边形的高等于三角形的高，三角形面积等于和它等底等高的平行四边形面积的一半 

③ 因为：平行四边形面积=底×高，所以：三角形面积=底×高÷2。即：S=ah÷2。

【3】梯形面积公式的推导过程？

① 用两个完全一样的梯形可以拼成一个平行四边形

② 平行四边形的底等于梯形的上底和下底的和，平行四边形的高等于梯形的高，梯形面积等于平行四边形面积的一半

③ 因为：平行四边形面积=底×高，所以：梯形面积=（上底＋下底）×高÷2。即：S=（a+b）h÷2。

【4】画图说明圆面积公式的推导过程

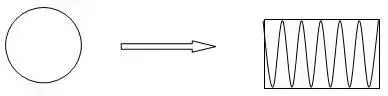
① 把圆分成若干等份，剪开后，拼成了一个近似的长方形。

② 长方形的长相当于圆周长的一半，宽相当于圆的半径。

③因为：长方形面积=长×宽，所以：圆面积=πr×r=πr2。即：S=πr2。 

十六、平面图形的周长和面积计算公式：

十七、常用数据：

一、长方体、正方体都有6个面，12条棱，8个顶点。

正方体是特殊的长方体。

二、圆柱的特征：一个侧面、两个底面、无数条高。

三、圆锥的特征：一个侧面、一个底面、一个顶点、一条高。

四、表面积：立体图形所有面的面积的和，叫做这个立体图形的表面积。

五、体积：物体所占空间的大小叫做物体的体积。

容器所能容纳其它物体的体积叫做容器的容积。

六、圆柱和圆锥三种关系：

 ① 等底等高：体积1︰3  

 ② 等底等体积：高1︰3  

 ③ 等高等体积：底面积1︰3

七、等底等高的圆柱和圆锥：

① 圆锥体积是圆柱的1/3，       

② 圆柱体积是圆锥的3倍，

③ 圆锥体积比圆柱少2/3，       

④ 圆柱体积比圆锥多2倍。

八、等底等高的圆柱和圆锥：锥1、差2、柱3、和4。

九、立体图形公式推导：

【1】圆柱的侧面展开后得到一个什么图形？这个图形的各部分与圆柱有何关系？（圆柱侧面积公式的推导过程）

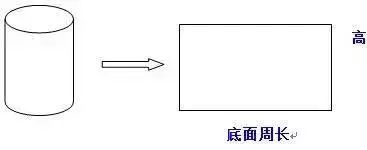
正方形的边长=圆柱的底面周长=圆柱的高。

【2】我们在学习圆柱体积的计算公式时，是把圆柱转化成以前学过的一种立体图形（近似的）进行推导的，请你说出这种立体图形的名称以及它与圆柱体有关部分之间的关系？

① 把圆柱分成若干等份，切开后拼成了一个近似的长方体。

② 长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高。

③ 因为：长方体体积=底面积×高，所以：圆柱体积=底面积×高。即：V=Sh。

【3】请画图说明圆锥体积公式的推导过程？

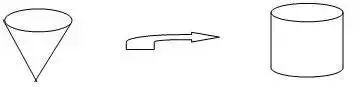
① 找来等底等高的空圆锥和空圆柱各一只。

② 将圆锥装满沙子，倒入圆柱中，发现三次正好装满，将圆柱里的沙子倒入圆锥中，发现三次正好倒完。

③ 通过实验发现：圆锥的体积等于和它等底等高的圆柱体积的三分之一；圆柱的体积等于和它等底等高的圆锥体积的三倍。即：V=1/3Sh。

十、立体图形的棱长总和、表面积、体积计算公式：  

一、变换图形位置的方法有平移、旋转等，在变换位置时，每个图形的相应顶点、线段、曲线应同步平移，旋转相同的角度。

二、不改变图形的形状，只改变它的大小时，通常要使每个图形的要素，如长方形的长与宽，三角形的底与高等同时按相同比例放大或缩小。

三、对称图形是对称轴两边的图形经对折后能够完全重合，而不是完全相同。

一、当我们处在实际生活及情景中，面对教短距离时，通常用上、下、前、后来描述具体位置。

二、当我们面对地图、方位图时，通常用东、西、南、北，南偏东、北偏东……来描述方向。

再结合所示比例尺计算出具体距离，把方向与距离结合起来确定位置。