5.1.1《用字母表示数》视频讲解

用字母表示数

1．用字母表示数。

在含有字母的式子里，字母中间的乘号可以记作“·”，也可以省略不写。数和字母相乘时，省略乘号后，一律将数写在字母前面。加号、减号除号以及数与数之间的乘号不能省略。数与数相乘时，乘号不可以省略。

2．用字母表示运算定律。

加法交换律是 a+b=b+a；

加法结合律是 (a+b)+c=a+(b+c)

乘法交换律是 ab=ba

乘法结合律是 (ab)c=a(bc)

乘法分配律是 (a+b)c=ac+bc。

3．用字母表示常见的数量关系及计算公式。

用含有字母的式子表示指定的数量，再把字母的取值代入式子中求值，只要在答中写出得数即可。

4、a×a可以写作a•a或a2 ，a2  读作a的平方。   

  2a表示a+a或2×a（1a=a这里的“1”我们不写）

方程的意义

方程：含有未知数的等式称为方程（★方程必须满足的条件：必须是等式 必须有未知数，两者缺一不可）。

1．方程与等式的区别。

含有未知数的等式叫做方程；方程一定是等式，而等式不一定是方程。

例：下列式子中，（   ）是方程。

A.3x+3>15        B.3x+3          C.3x+3=15

答案：C

2．等式的性质。

等式两边同时加上或减去相同的数，同时乘或除以相同的数(0除外)，左右两边仍然相等。

3、两个数相加，和都相同，一个加数越小，另一个加数就越大。

两个数相减，差都相同，减数越大，被减数也越大。

两个数相乘，积都相同，一个因数越小，另一个因数就越大。

两个数相除，商都相同，除数越大，被除数就越大。

解方程

1．方程的解与解方程。

使方程左右两边相等的未知数的值，叫做方程的解。求方程的解的过程叫做解方程。 

“方程的解”是一个数，是使等号左右两边相等的未知数的值；“解方程”是指演算过程。

2．解形如X±a=b 和 aX=b 的方程。

依据等式性质来解此类方程。解方程时要注意写清步骤，等号对齐。

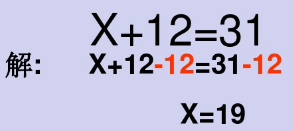
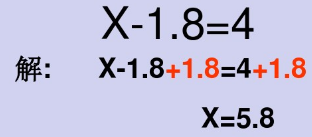
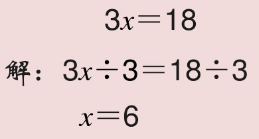
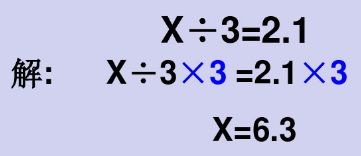
3．验算。检验是不是方程的解，把解代入原方程的左边算出得数，再算出右边的得数，如果左右两边的得数相等，那么这个解就是原方程的解。

检验：把 x=81代入原方程，得：

方程左边=2×81+55=217=方程右边

所以， x=81是原方程的解。

4、解方程原理：

 A、等式两边同时加或减相等的数，等式不变。

 B、等式两边同时乘或除以相同的数（0 除外），等式不变。

 C、四则运算的意义及性质：

  10个数量关系式： 

@ 加法:

  和=加数+加数 ；   

一个加数=和 - 另一个加数

@ 减法：  

  差=被减数 - 减数 ；    

  被减数=差+减数 ；    

  减数=被减数 - 差

@乘法： 

  积=因数×因数 ；      

  一个因数=积÷另一个因数

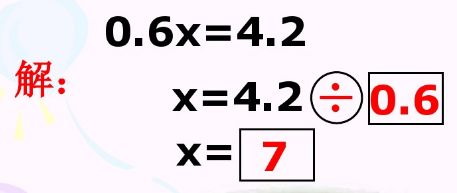
@ 除法：

  商=被除数÷除数 ；    

  被除数=商×除数 ；    

  除数=被除数÷商

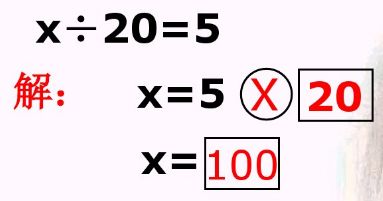
5、在列方程解决问题时，我们应统一单位，在方程求出的解的后面不写单位名称。

列方程解决问题 

方法步骤：

1、读题、分析题意（从要求入手）。

【找出已知信息（包括隐含信息剔除无用信息）和未知(即要求信息)；注意单位是否一致；不一致先转化】 

2、解：设未知数。

【有两个未知数，通常设小的那个，另一个用含设的未知数的关系式表示。】 

和倍或差倍应用题的解答方法： 设一倍的量为x，另一个量根据倍数关系表示为几x。再根据两个量的和或差列出方程。

例如：

3、思考并列出方程。 

【根据题意和找出的信息建立已知和未知的等量关系列出方程。】     

4、解方程。 

5、检验反思后作答。    （方程的解不能带单位）

例：妈妈买了2.9千克香蕉，她付给售货员30元，找回9.7元。每千克香蕉多少元？

解答：

答：每千克香蕉7元。

方程解法与算术解法的区别：