2024中考数学复习 | 各类计算题型之【反比例】,有答案,收藏练习

【一】如图，菱形ABCD的边AD与x轴平行，A、B两点的横坐标分别为1和3，反比例函数y＝3/x的图象经过A、B两点，求菱形ABCD的面积.

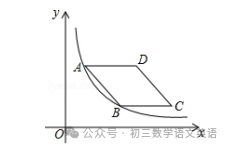
解：作AH⊥BC交CB的延长线于H，

∵反比例函数y＝3、x的图象经过A、B两点，A、B两点的横坐标分别为1和3，

∴A、B两点的纵坐标分别为3和1，

即点A的坐标为（1，3），点B的坐标为（3，1），

∴AH＝3﹣1＝2，BH＝3﹣1＝2，

由勾股定理得，AB＝√2²+2²＝2√2，

∵四边形ABCD是菱形，

∴BC＝AB＝2√2，

∴菱形ABCD的面积＝BC×AH＝4√2

【二】如图，矩形ABCD在第一象限，AB在x轴的正半轴上，AB＝3，BC＝1，直线y=1/2x﹣1经过点C交x轴于点E，双曲线y＝k/x经过点D，求k的值.

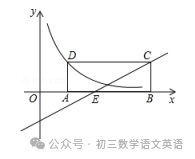
解：根据矩形的性质知点C的纵坐标是y＝1，

∵直线y＝1/2x﹣1经过点C，

∴1＝1/2x﹣1，

解得，x＝4，

即点C的坐标是（4，1）．

∵矩形ABCD在第一象限，AB在x轴正半轴上，AB＝3，BC＝1，∴D（1，1），

∵双曲线y＝k/x经过点D，

∴k＝xy＝1×1＝1，即k的值为1．

【三】如图，△ABC三个顶点分别在反比例函数y＝1/x，y＝k/x的图象上，若∠C＝90°，AC∥y 轴，BC∥x 轴，S_△ABC＝8，求k的值.

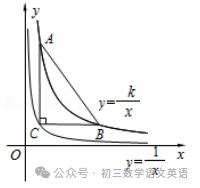
解：设点C的坐标为（m，1/m），

则点A的坐标为（m，k/m），

点B的坐标为（km，1/m），

∴AC＝k/m﹣1/m＝k1/m，

BC＝km﹣m＝（k﹣1）m，

∵S_△ABC＝1/2AC•BC＝1/2（k﹣1）²＝8，

∴k＝5或k＝﹣3．

∵反比例函数y＝k/x在第一象限有图象，

∴k＝5．

【四】如图，点A是双曲线y＝在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，求这个函数的解析式.

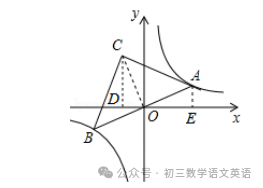
解：如图，连结OC，作CD⊥x轴于D，AE⊥x轴于E，

∵A点、B点是正比例函数图象与双曲线y＝6/x的交点，

∴点A与点B关于原点对称，

∴OA＝OB，

∵△ABC为等腰直角三角形，

∴OC＝OA，OC⊥OA，

∴∠DOC+∠AOE＝90°，

∵∠DOC+∠DCO＝90°，

∴∠DCO＝∠AOE，

∵在△COD和△OAE中，

DCO＝∠AOE，∠COD＝∠AEO，OC=OA

∴△COD≌△OAE（AAS），

设A点坐标为（a，6/a），

则OD＝AE＝6/a），CD＝OE＝a，

∴C点坐标为（﹣6/a，a），

∵﹣6/a•a＝﹣6，

∴点C在反比例函数y＝y＝﹣6/x（x＜0）图象上．

【五】如图，在平面直角坐标系xOy中，点A（3，2）在反比例函数y＝k/x（x＞0）的图象上，点B在OA的延长线上，BC⊥x轴，垂足为C，BC与反比例函数的图象相交于点D，连接AC，AD．

（1）求该反比例函数的解析式；

解：∵点A（3，2）在反比例函数y＝k/x（x＞0）的图象上，

∴k＝3×2＝6，

∴反比例函数y＝6/x；

答：反比例函数的关系式为：y＝6/x；

（2）若S_△ACD＝3/2，设点C的坐标为（a，0），

①求点D的坐标；

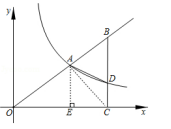
解：过点A作AE⊥OC，垂足为E，连接AC，

设直线OA的关系式为y＝kx，将A（3，2）代入得，k＝2/3，

∴直线OA的关系式为y＝2/3x，

∵点C（a，0），

把x＝a代入y＝2/3x，得：y＝2/3a，

把x＝a代入y＝6/x，得：y＝6/a，

∴B（a，2/3a），即BC=2/3a，

∴D（a，6/a），即CD＝6/a，

∵S_△ACD＝3/2，

∴1/2CD•EC＝3/2，

即1/2×6/a×（a﹣3）＝3/2，解得：a＝6，

∴D（6，1）；

②求线段BD的长．

解：BD＝BC﹣CD＝2/3a-6/a＝3；

答：线段BD的长为3．

点个在看你最好看