中考复习课:第五章四边形第二节矩形、菱形和正方形之菱形
中考复习课:第五章四边形
第二节矩形、菱形和正方形之菱形
本章节对应课本内容
八年级下册P52-P69(人教版)
考点揭秘
历年真题
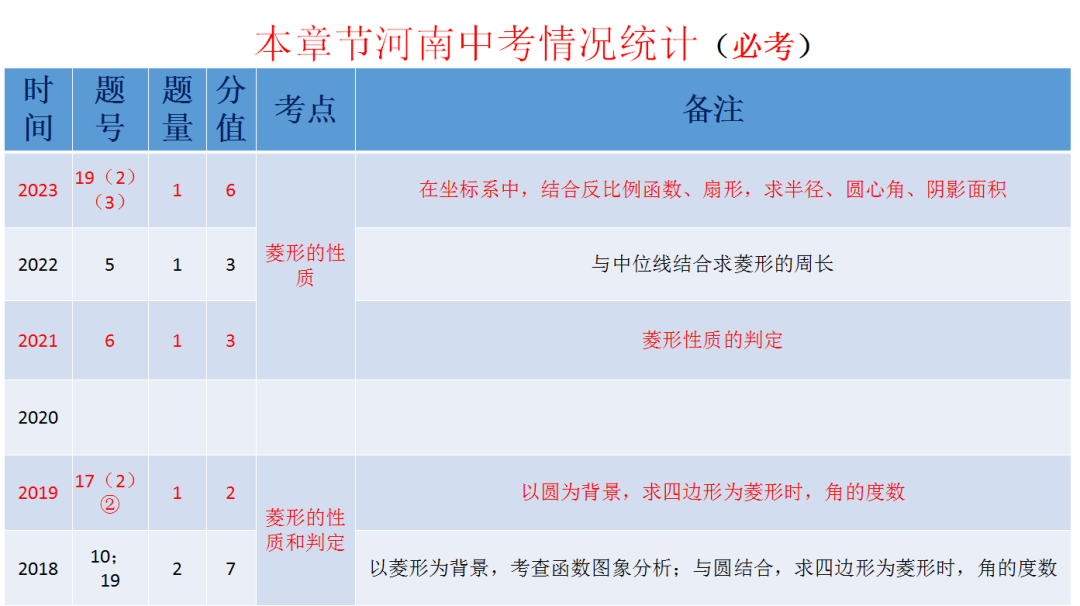
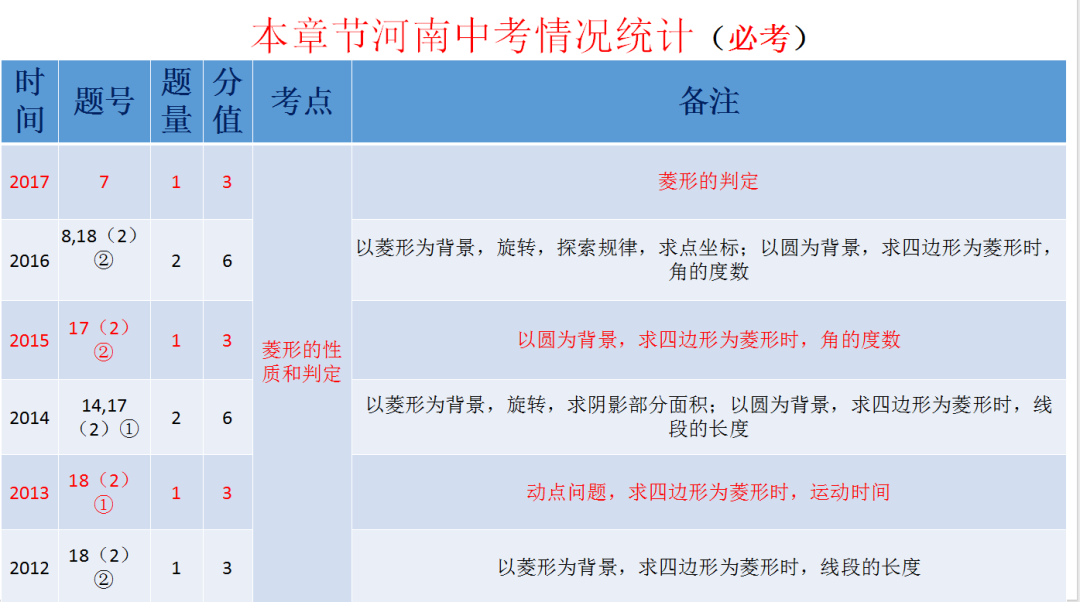
2023年河南中考本章节试题
19.(9分)(2023•河南)小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数 图象上的点 和点 B 为顶点,分别作菱形 AOCD 和菱形 OBEF ,点 D,E 在 x 轴上,以点 O 为圆心, OA 长为半径作 ,连接 BF .
5.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为CD的中点.若OE=3,则菱形ABCD的周长为( ) 17. (9分)如图,在 △ ABC 中,BA= BC,∠ABC =90°.以 AB 为直径的半圆 O 交 AC 于点 D,点E 是 ①若 AB =4,且点 E 是 的中点,则 DF 的长为________; ②取 的中点 H,当 ∠ EAB 的度数为________时,四边形 OBEH 为菱形.
10. 如图①,点 F 从菱形 ABCD 的顶点 A 出发,沿 A → D → B 以1 cm/s的速度匀速运动到点 B .图②是点 F 运动时,△ FBC 的面积 y (cm2 )随时间 x (s)变化的关系图象,则 a 的值为 ( )
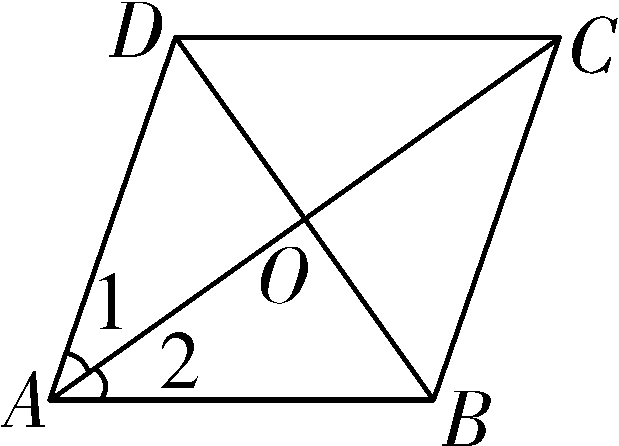
19. (9分)如图, AB 是⊙ O 的直径, DO ⊥ AB 于点 O ,连接 DA 交⊙ O 于点 C ,过点 C 作⊙ O 的切线交 DO 于点 E ,连接 BC 交 DO 于点 F . ①当∠ D 的度数为________时,四边形 ECFG 为菱形 ; ②当∠ D 的度数为________时,四边形 ECOG 为正方形. 7. 如图,在▱ ABCD 中,对角线 AC,BD 相交于点 O ,添加下列条件不能判定▱ ABCD 是菱形的只有 A. AC ⊥ BD B. AB = BC C. AC = BD D. ∠1=∠2 8. 如图,已知菱形 OABC 的顶点 O (0,0), B (2,2),若菱形绕点 O 逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点 D 的坐标为( )
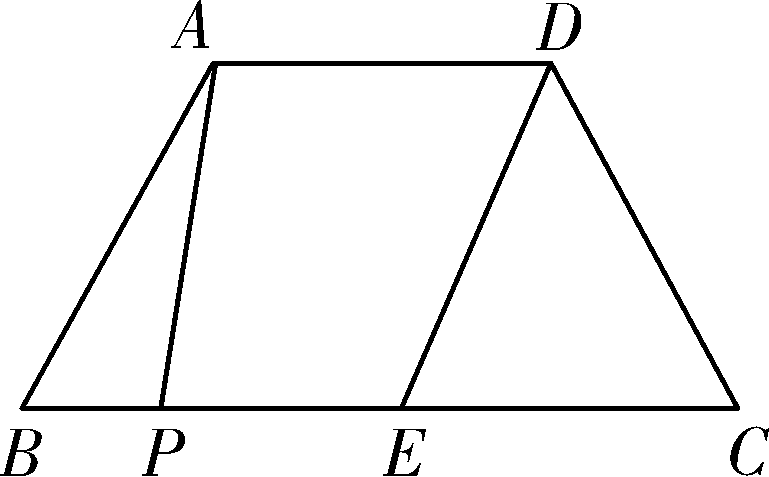
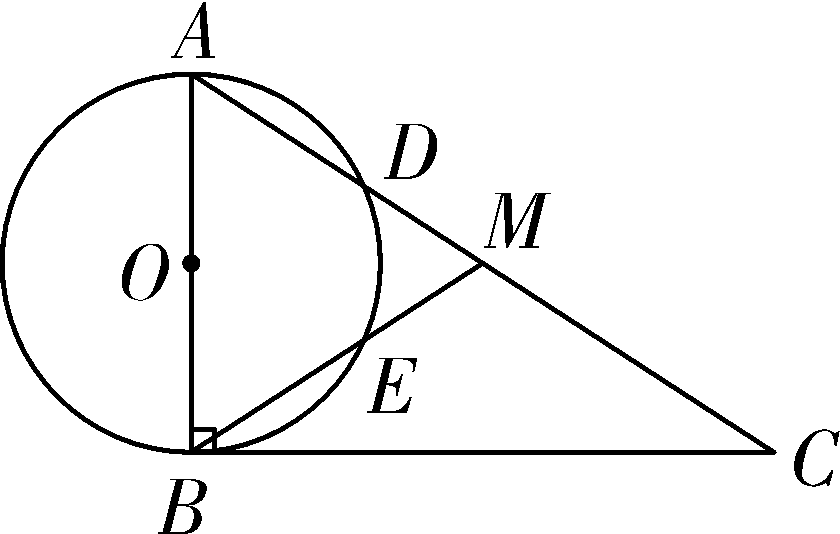
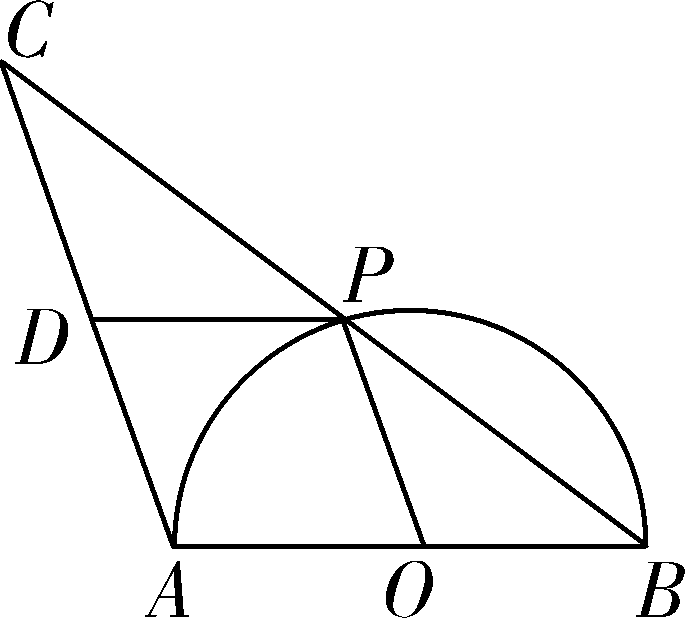
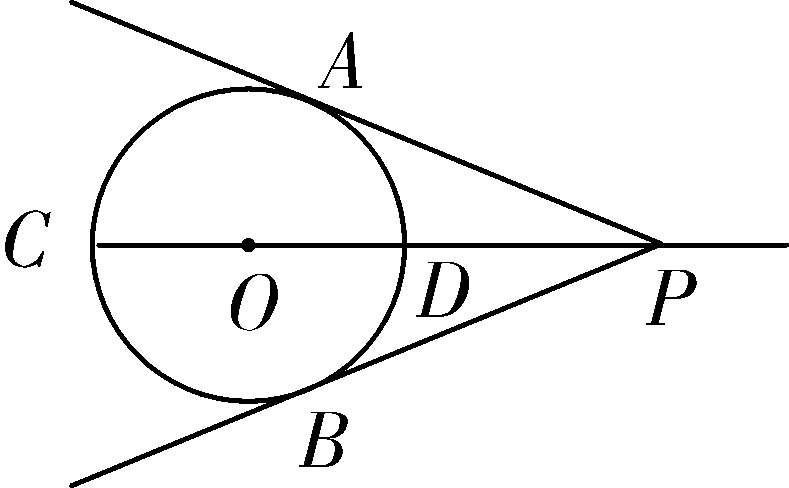
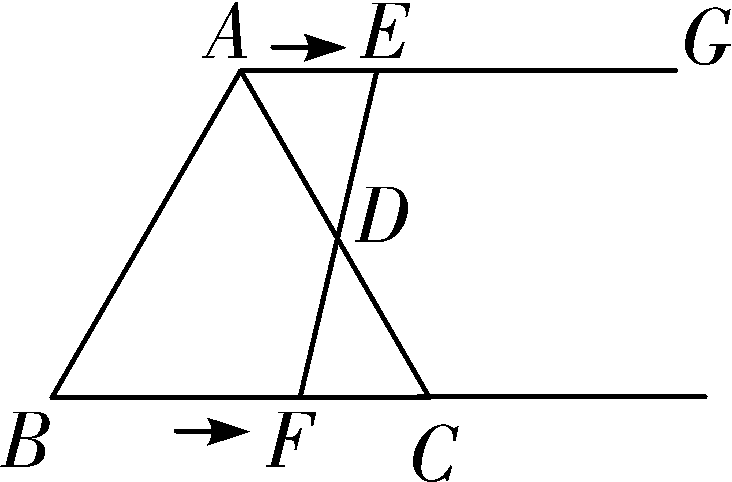
18. (9分)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E. ①若AB=6,当AD=2DM时,DE=______; ②连接OD,OE,当∠A的度数为______时,四边形ODME是菱形. 17. (9分)如图, AB 是半圆 O 的直径,点 P 是半圆上不与点 A,B 重合的一个动点,延长 BP 到点 C ,使 PC = PB,D 是 AC 的中点,连接 PD,PO . ①若 AB =4,则四边形 AOPD 的最大面积为________; ②连接 OD ,当∠ PBA 的度数为________时,四边形 BPDO 是菱形. 14. 如图,在菱形 ABCD 中, AB =1,∠ DAB =60°,把菱形 ABCD 绕点 A 顺时针旋转30°得到菱形 AB ′ C ′ D ′,其中点 C 的运动路径为 ,则图中阴影部分的面积为________. 17. (9分)如图,CD是⊙O的直径,且CD=2 cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为点A、B. (1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形. ①当DP=________cm时,四边形AOBD是菱形; ②当DP=________cm时,四边形AOBP是正方形. 18. (9分)如图,在等边三角形ABC中,BC=6 cm. 射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,同时点F从点B出发沿射线BC以2 cm/s 的速度运动,设运动时间为t(s). (1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF; ①当t为________s时,四边形ACFE是菱形; ②当t为________s时,以A、F、C、E为顶点的四边形是直角梯形. 18. (9分)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN. (2)填空:①当AM的值为________时,四边形AMDN是矩形; ②当AM的值为________时,四边形AMDN是菱形 . 22.(10分)如图,在Rt△ABC中,∠B=90°,BC= ∠C=30°.点D从点C出发沿CA方向以每秒2 个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1 个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF. (2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由; (3)当t为何值时,△DEF为直角三角形?请说明理由. 19. (9分)如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD= ∠C=45°,点P是BC边上一动点,设PB的长为x. (1)当x的值为________时,以点P、A、D、E为顶点的四边形为直角梯形; (2)当x的值为________时,以点P、A、D、E为顶点的四边形为平行 四边形; (3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由. 参考资料
复习课:第五章四边形第2节矩形、菱形和正方形2
菱形必考!菱形的性质与判定三大题型均有涉及.(1)菱形的性质在填空题中考查,考查的形式为菱形旋转求阴影部分面积.(2)菱形的判定在选择题和解答题中考查,考查的形式有:①识别不能判定菱形的条件;②以简单几何图形(三角形、菱形、梯形、半圆、圆)为背景,结合动点或旋转操作来考查菱形的判定.
拿着规律,认真把河南中考相应内容在公众号“轩波数学课糖”里好好读一读,练一练,想一想。切忌浮躁。
版权声明: 本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!


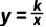 图象上的点
图象上的点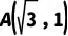 和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作
和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作 ,连接BF.
,连接BF.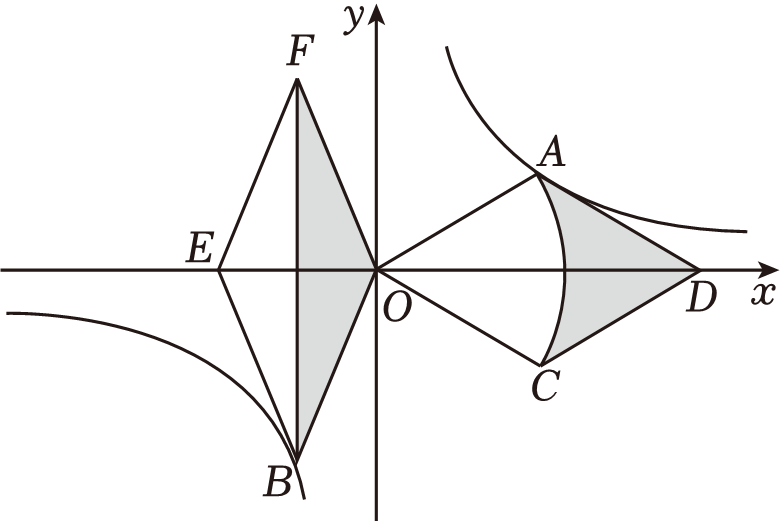
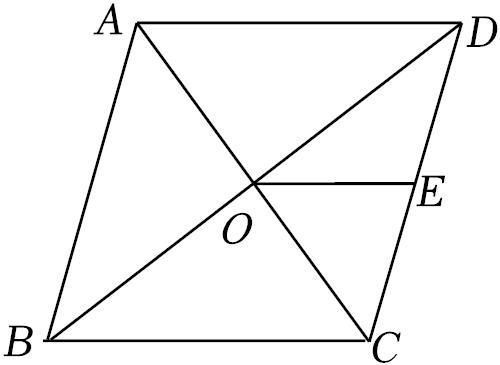
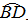
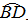 的中点,则DF的长为________;
的中点,则DF的长为________;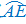 的中点H,当∠EAB的度数为________时,四边形OBEH为菱形.
的中点H,当∠EAB的度数为________时,四边形OBEH为菱形.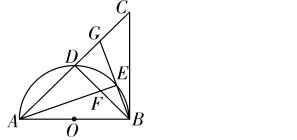
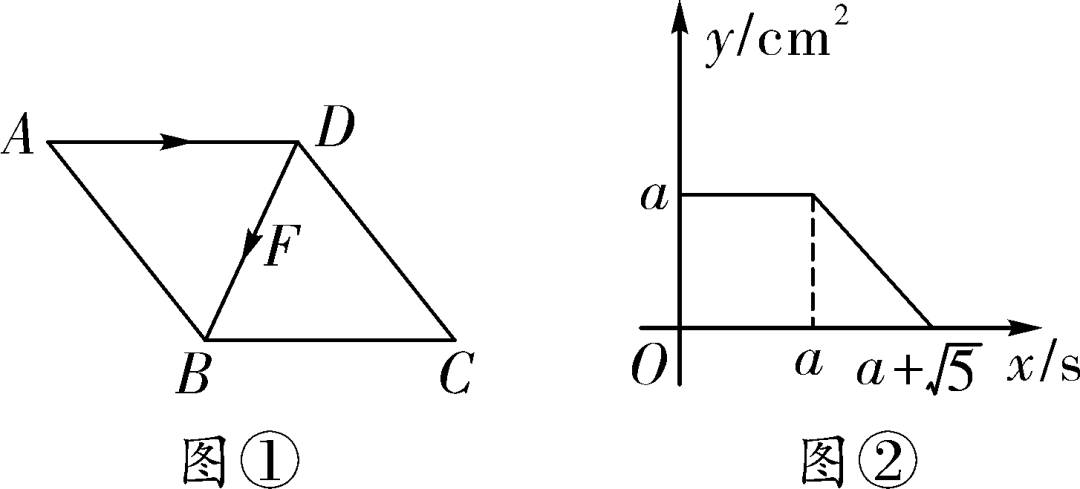

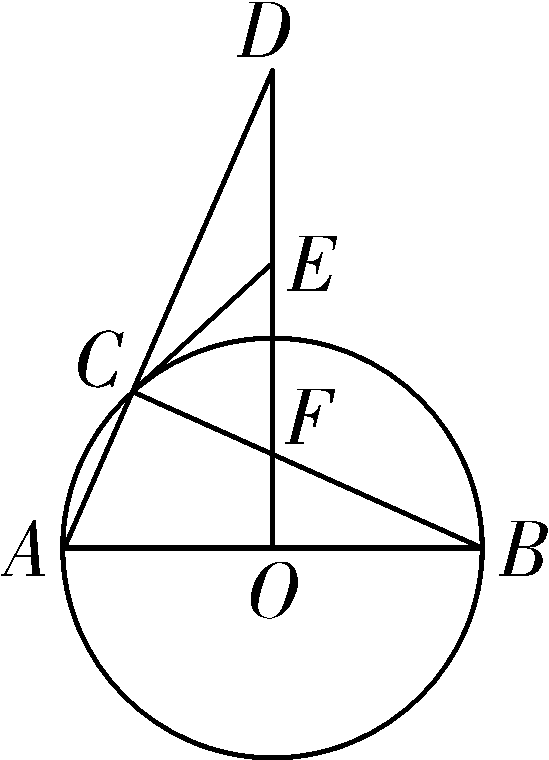
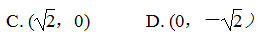
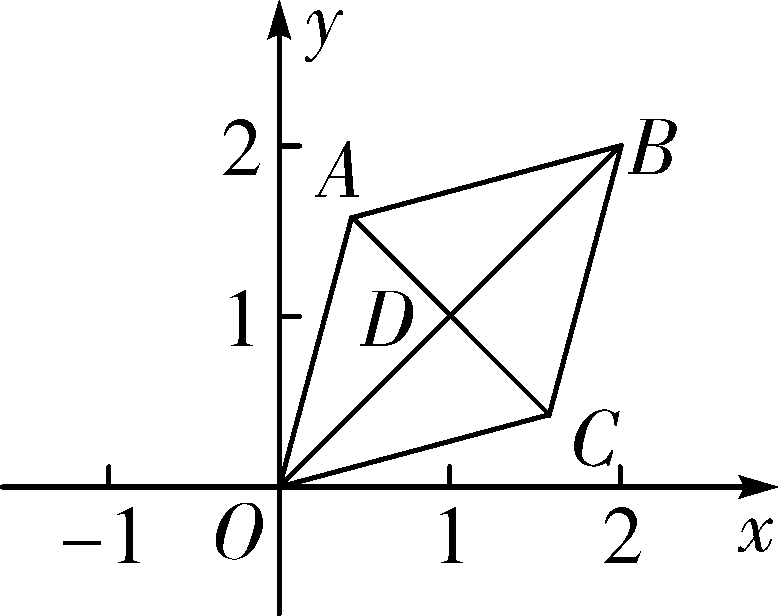
 ,则图中阴影部分的面积为________.
,则图中阴影部分的面积为________.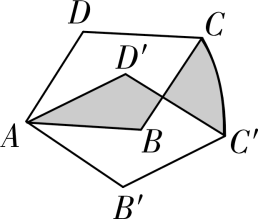

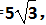 ∠C=30°.点D从点C出发沿CA方向以每秒2 个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1 个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
∠C=30°.点D从点C出发沿CA方向以每秒2 个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1 个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.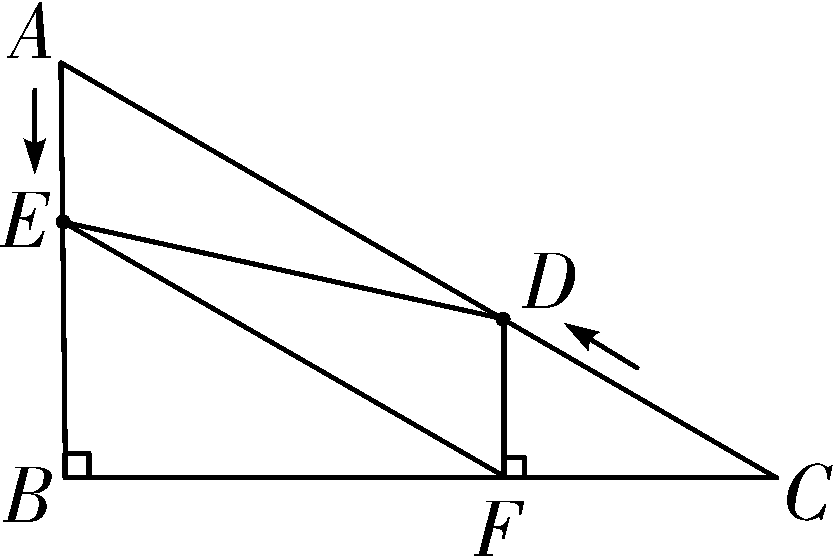
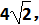 ∠C=45°,点P是BC边上一动点,设PB的长为x.
∠C=45°,点P是BC边上一动点,设PB的长为x.