杨德发:问解2021年高考数学新课标Ⅱ卷第17题

欢迎转发分享，让更多的中国人因您的转发而受益！

杨德发：问解2021年高考数学新课标Ⅱ卷第17题

文/杨德发

校对/于海玲

摘要：解题规律：所有学科的试题均可用提问法和作图法结合又快又准地求解。用提问法(结合作图法)，能将所有试题变成简单题。

关键词：高考数学命题规律、解题规律、提问法、作图法、自问等。

2021年高考数学新课标Ⅱ卷17.（12分）记S_n是公差不为0的等差数列{a_n}的前n项和，若a₃=S₅，a₂a₄=S₄.

(1)求数列{a_n}的通项公式a_n；

(2)求使S_n>a_n成立的n的最小值.

问1：能否求出a₃=？

思1：……（略，下同）

忆1：……（略，下同）

答1：能，由等差数列的性质有：

S₅=5a₃，

代入a₃=S₅有：a₃=5a₃，

所以a₃=0。

问2：设等差数列的公差为d，能否求出d=？

答2：能，

a₂a₄=(a₃-d)(a₃+d)=-d²，

S₄=a₁+a₂+a₃+a₄=(a₃-2d)+(a₃-d)+a₃+(a₃+d)=-2d，

代入a₂a₄=S₄有：-d²=-2d，

解得：d=2。（公差不等于0）

问3：能否求出等差数列的通项a_n=？

答3：能，由通项公式有：

a_n=a₃+(n-3)d=2n-6。

问4：能否求出a₁=？

答4：能，a₁=2×1-6=-4。

问5：能否求出等差数列的前n项和S_n=?

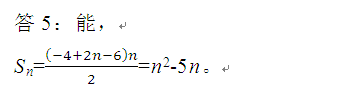
问6：能否求出使S_n>a_n成立的n的最小值？

答6：能，

n²-5n>2n-6，

（n-1）(n-6)>0，

解得：n<1或n>6，

又因为n为正整数，所以n的最小值为7。

本题的类型：数列问题的求解。

本题考查的主要知识：等差数列的通项公式、求和公式、不等式等。

本题考查的解题方法：提问法、作图法（若必要的话）。

本题考查的主要能力：提问能力、记忆能力、理解能力、作图能力、运用数学工具处理数学问题的能力（运算能力、数学语言表达能力）等。

本题的难度等级：中。本题难度D=Q²=6²=36，Q表示小问题的个数，也表示解题的步数。若学生基础差，还要提更多的小问。

本题的区分度：对中分段学生有一定的区分度。

本题对高中数学考、学、教、练、研、管的启示：等差数列、等比数列公式要记牢。

点评：问解才是解题的最一般方法。我们对2021年高考数学新课标Ⅱ卷的每一道题来个“小题大做”，把每一道题变得非常简单。杀鸡用牛刀，有何不可？

练习（一分学，九分练）：

1.抄写：大脑认知功能的本质是：自问→自思→自忆→自答。解决问题也是用提问。

2.请您去训练自己的自问能力！

【声明：欢迎杂志、报纸、公众号转刊！欢迎写作时引用！欢迎工作中采用！欢迎选编入教师、学生、家长读本！均须注明出处】

（写于：2024年3月1日周五）

[杨德发，男，汉族，1966年3月出生于重庆市梁平区仁贤街道五一社区大竹林，1987年7月参加工作，教师培训中心教（jiāo）研员，教育实干家，教师队伍建设实干家，2003年5月加入中国共产党，重庆师范学院物理系毕业，理学学士，中国物理学会会员（发现物理规律“杨德发定理”），重庆市重点课题《学本式教师培训资源开发研究》课题组负责人，获奖100余次，在杂志上发表论文100余篇，在公众号上发表文章3100余篇，请关注《提问学Quizoloɡy》，公众号：Quizoloɡy，手机：18983078247微信：cq-ydfy×s。于海玲，小学数学教（jiāo）研员，牡丹江市第二期“名优工程”骨干型教师、小学数学学科带头人，执教的《数学广角——问题解决》获牡丹江市小学数学学科优质课竞赛特等奖。手机：13199337376微信：sd867324492]

扫描关注公众号！投稿加微信：cq-ydfy×s