中考数学冲刺复习之几何模型对角互补的三种模型
中考数学冲刺复习
几何模型
对角互补的三种模型
【对角互补模型】即四边形或多边形构成的几何图形中，相对的角互补。主要分为含90°与120°的两种对角互补类型。该题型常用到的辅助线主要是顶定点向两边做垂线，从而证明两个三角形全等或者相似。
【模型一】含90°的全等型
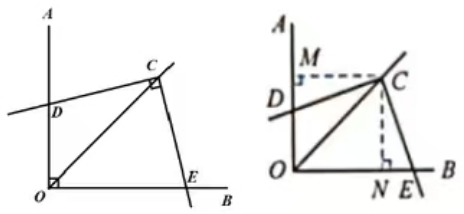
1.如图，已知∠AOB=∠DCE=90°,OC平分∠AOB.
则可以得到如下几个结论：
①CD=CE,②OD+OE=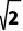
OC,③S△DCE=S△OCD+S△OCE=1/2OC2.
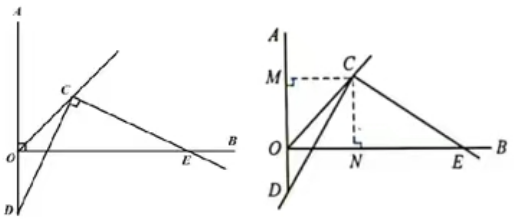
2.如图，已知∠DCE的一边与AO的延长线交于点D,∠AOB=∠DCE=90°,OC平分∠AOB.
则可得到如下几个结论：
①CD=CE,②OE-OD=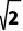OC,③S△COE-S△COD=1/20C2.
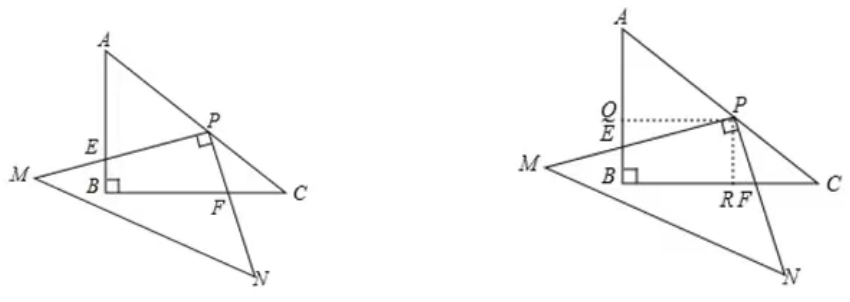
例1.如图，在RtΔABC中，∠ABC=90°,AB=3,BC=4,RtΔMPN,∠MPN=90°,点P在AC上，PM交AB于点E,PN交BC于点F,当PE=2PF时，AP= .
数学陈老师:
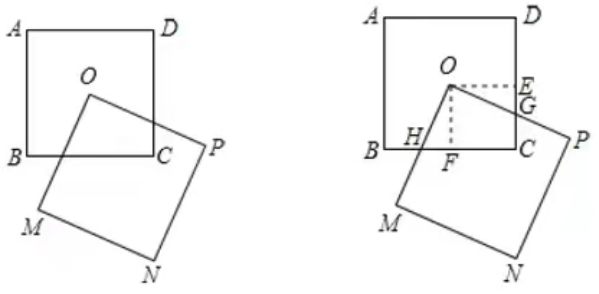
【变式训练1】如图，正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心，正方形OMNP绕O点旋转，证明：无论正方形OMNP旋转到何种位置，这两个正方形重叠部分的面积总是一个定值，并求这个定值。
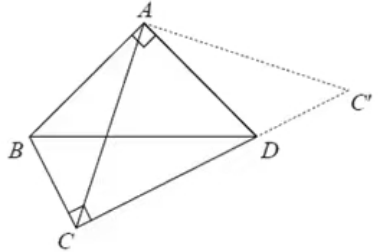
【变式训练2】四边形ABCD被对角线BD分为等腰直角ΔABD和直角ΔCBD,其中∠A和∠C都是直角，另一条对角线AC的长度为2,求四边形ABCD的面积．
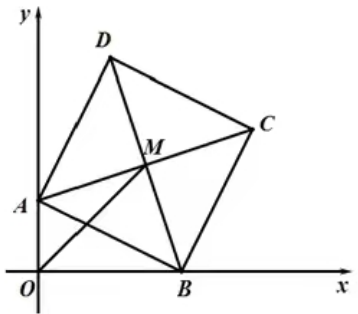
【变式训练3】如图，在平面直角坐标系中，正方形ABCD顶点A(0, 2),B点在x轴上，对角线AC、BD交于点M,OM=3,则点C的坐标为 .
数学陈老师:
【模型二】含60°与120°的全等型
如图，已知∠AOB=2∠DCE=120°,OC平分∠AOB.
则可得到如下几个结论：
①CD=CE,②OD+OE=OC,③SΔCOD+SΔCOE=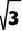
/4OC2
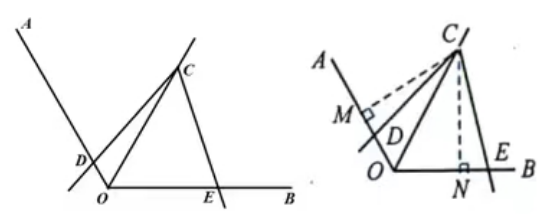
例2．如图，在ΔABC中，AB=AC,点D为BC的中点，点E、F分别在AB、AC上，若∠A=60°, ∠EDF+∠A=180°,求证：BE+CF=1/2AB.
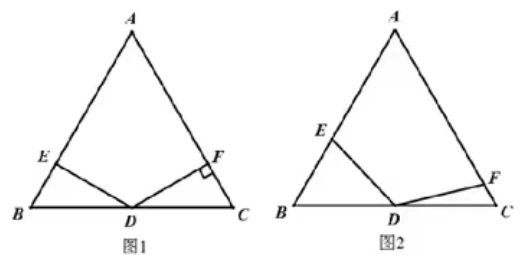
【变式训练】在等边ΔABC中，点D是线段BC的中点，∠EDF=120°,射线DE与线段AB相交于点E,射线DF与线段AC(或AC的延长线）相交于点F.
（1)如图1,若DF⊥AC,直接写出DE与AB的位置关系；
（2)如图2,将（1)中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F,求证：DE=DF;
（3)在∠EDF绕D顺时针旋转过程中，直接用等式表示线段BE、CF、AB之间的数量关系。
数学陈老师:
【模型三】相似型
例3.
【提出问题】
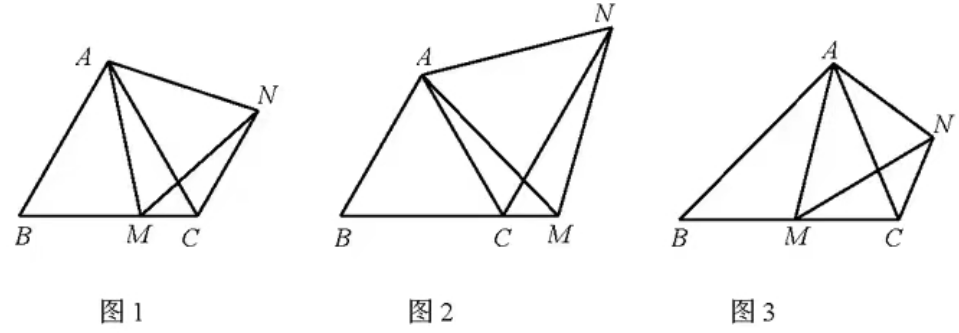
（1)如图1,在等边ΔABC中，点M是BC上的任意一点（不含端点B、C),连结AM,以AM为边作等边ΔAMN,连结CN. 求证：BM=CN.
【类比探究】
（2)如图2,在等边ΔABC中，点M是BC延长线上的任意一点（不含端点C),其它条件不变，（1)中结论BM=CN还成立吗？请说明理由．
【拓展延伸】
（3)如图3,在等腰ΔABC中，BA=BC,AB=6,AC=4,点M是BC上的任意一点（不含端点B、C),连结AM,以AM为边作等腰ΔAMN,使顶角∠AMN=∠ABC. 连结CN. 试探究BM与CN的数量关系，并说明理由。
数学陈老师:
【达标训练】
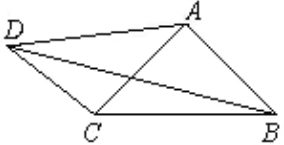
1.如图所示，在四边形ABCD中，AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
2、如图，在ΔABC中，∠ABC=60°,AB=2,BC=8,以AC为腰，点A为顶点作等腰ΔACD,且∠DAC=120°,则BD的长为 .
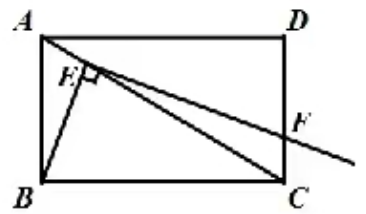
3.如图，在矩形ABCD中，AB=3,BC=4,点E在对角线AC上，连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则EF/BE= .
4.如图，在正方形ABCD中，对角线AC、BD相交于点O,E、F分别为AD、CD上的点，若AE=4,CF=3,且OE⊥OF,求EF的长．
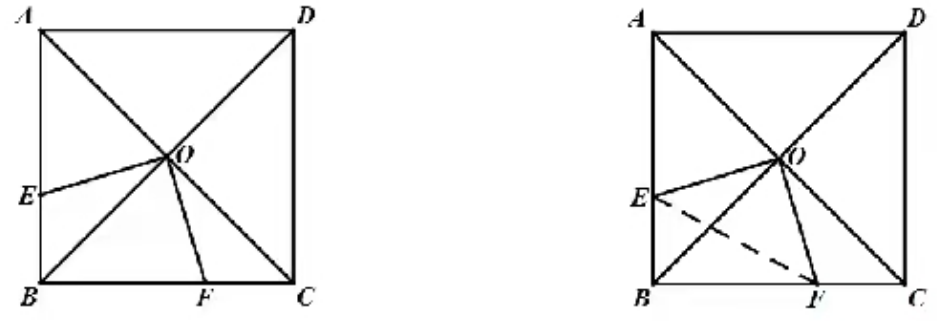
数学陈老师:
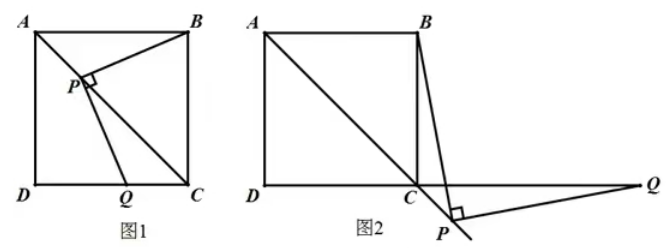
5.如图，在正方形ABCD中，AC是对角线，今有较大的直角三角板，一边始终经过点B,直角顶点P在射线AC上移动，另一边交DC于Q.
（1)如图1,当点Q在DC边上，猜想并写出PB与PQ所满足的数量关系，并加以说明；
（2)如图2,当点Q落在DC延长线上时，猜想并写出PB与PQ满足的数量关系，请证明你的猜想。
点赞+关注
天天学习不迷路
赞赏后请留言
可提供答案解析
空白电子文档
