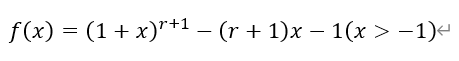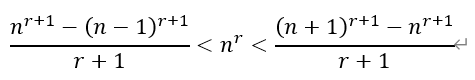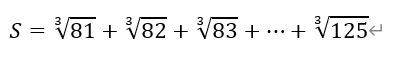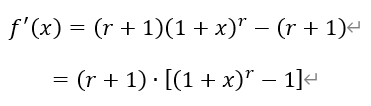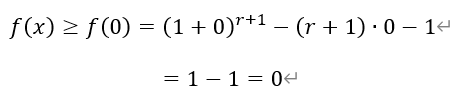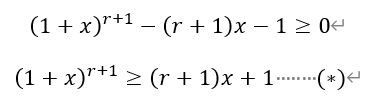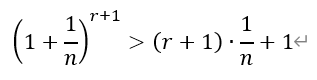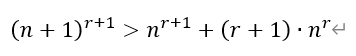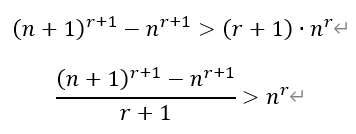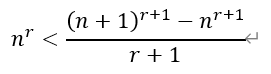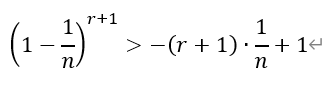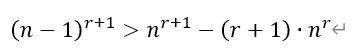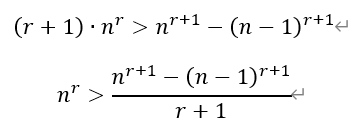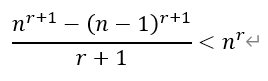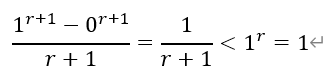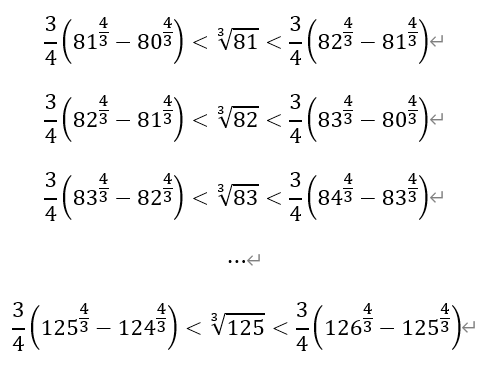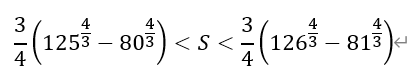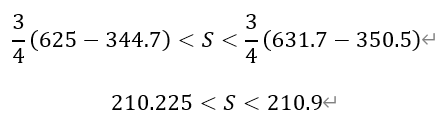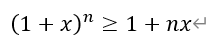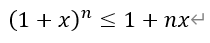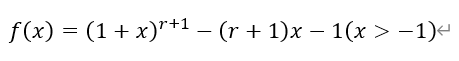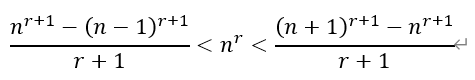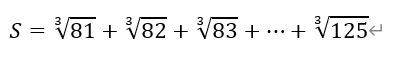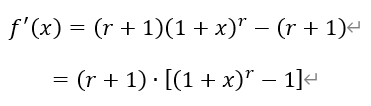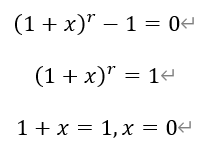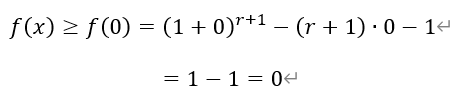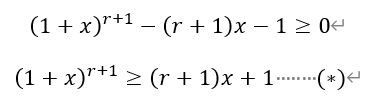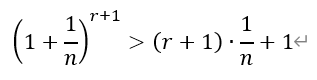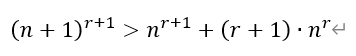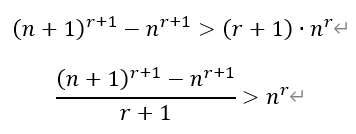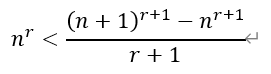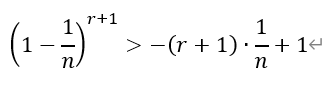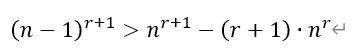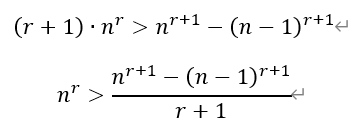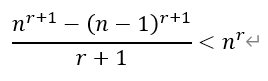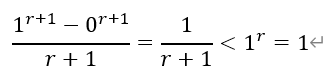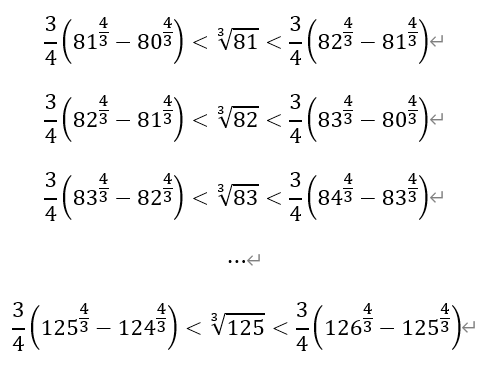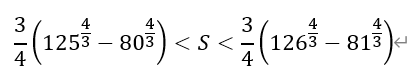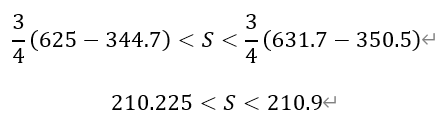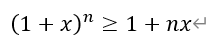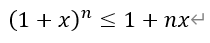2024年新高考第19题之伯努利不等式
四季读书网
57

[引言]全国新高考数学试卷第19题的议论众多。进入3月以来,各地纷纷组织了高三的一模考试,现将酝酿后的典型题目整理如下。[题目](2013年,湖北高考,理数22)设n为正整数,r为正有理数。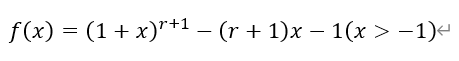
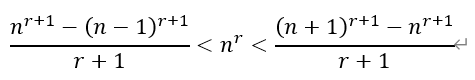
(III)设x∈R,记[x]不小于x的最小整数,例如[2]=2,[π]=4,[-3/2]=-1。令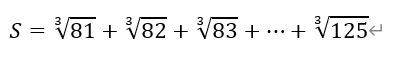
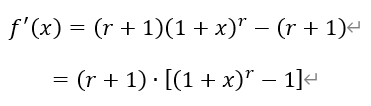
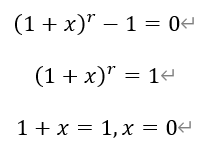
因此,函数f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增。即在x=0处取得最小值,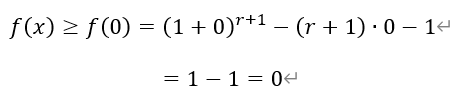
2)由1)可知,当x>-1时,f(x)≥f(0),当且仅当x=0时取等号。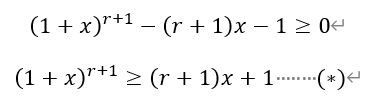
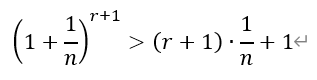
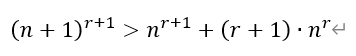
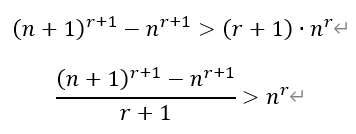
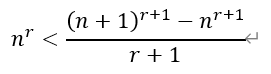
ⅱ)当n>1时,在(*)式中,令x=-1/n,其中n∈N*,则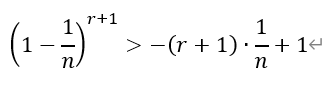
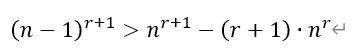
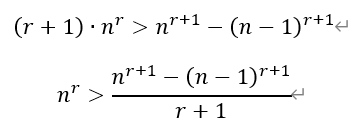
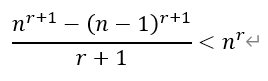
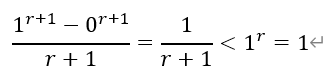
3)根据2)的结论,令r=1/3,n分别取81、82、83、…、125,有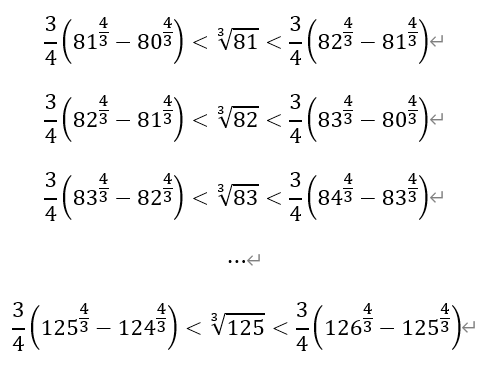
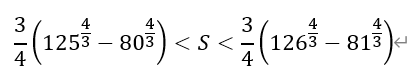
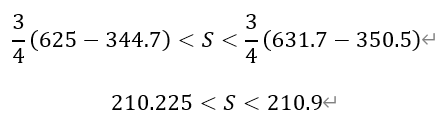
[后记]本题是2013年湖北高考理科数学的压轴解答题,时至今日仍熠熠生辉,让很多所谓的新高考第19题创新题黯然失色。其中第三问的答案为211,颇有预祝各位考生考上“211”高校的深刻寓意,令人唏嘘。本题实际上由伯努利不等式演变而来。所谓伯努利不等式是指: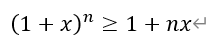
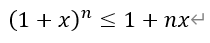
其中,若n为正整数,则不等式右侧就是二项展开式的前两项,显然成立。若n为实数的情况,可以用微分证明,本文从略。伯努利不等式形式简洁,可以将高次幂变为低次幂,极大的简化运算。它常被用作证明其它不等式的关键步骤,在数学分析中有着广泛的应用。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!